通过强化学习解决河内塔难题。
在安装了 Numpy 和 Pandas 的 Python 环境中,运行脚本hanoi.py以生成结果部分中显示的三个图。例如,可以轻松地修改脚本以使用不同数量的磁盘N来玩游戏。
最近,随着谷歌 Deepmind 的 AlphaGo 击败了职业人类围棋棋手,强化学习重新引起了人们的兴趣。在这里,一个更简单的难题得到了解决:汉诺塔游戏。该实现遵循 Watkins 和 Dayan [1] 最初提出的 Q 学习算法。
河内塔游戏由三个钉子和许多不同大小的可以滑到钉子上的圆盘组成。拼图开始时,所有圆盘按升序堆叠在第一个钉子上,最大的在底部,最小的在顶部。游戏的目标是将所有圆盘移动到第三个钉子上。唯一合法的举动是将最上面的圆盘从一个钉子移到另一个钉子上,但限制是永远不能将一个圆盘放置在较小的圆盘上。图 1 显示了 4 个磁盘的最佳解决方案。

图 1. 4 个圆盘的河内塔拼图的动画解决方案。 (来源:维基百科)。
遵循 Anderson [2],我们用元组表示游戏的状态,其中第 i个元素表示第i个磁盘位于哪个桩上。磁盘按大小递增的顺序进行标记。因此,初始状态为 (111),所需的最终状态为 (333)(图 2)。
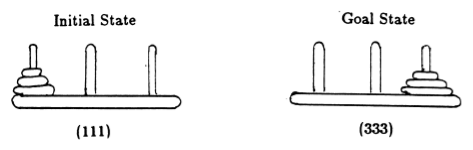
图 2.具有 3 个圆盘的河内塔谜题的初始状态和目标状态。 (来自[2])。
谜题的状态以及它们之间对应于合法移动的转换形成了谜题的状态转换图,如图 3 所示。
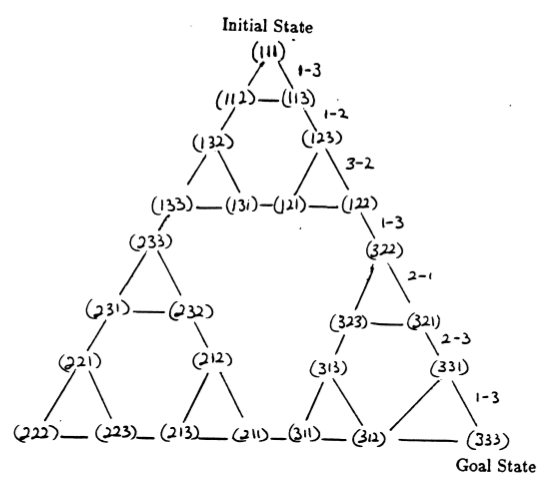
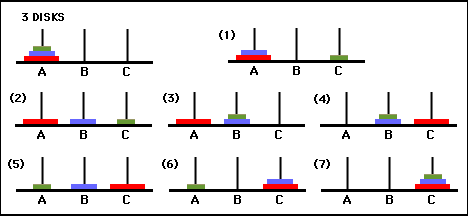
图 3.三盘河内塔谜题的状态转换图(上图)和相应的最佳 7 步解(下图),该解遵循图右侧的路径。 (来自 [2] 和 Mathforum.org)。
解决汉诺塔谜题所需的最小移动次数为 2 N - 1,其中N是圆盘的数量。因此,对于N = 3,可以通过 7 次移动来解决该难题,如图 3 所示。在下一节中,我们将概述如何通过 Q 学习来实现这一点。
R和“行动价值”矩阵Q程序的第一步是生成一个奖励矩阵R ,它捕获游戏规则并为获胜者提供奖励。为简单起见,图 4 中显示了N = 2磁盘的奖励矩阵。
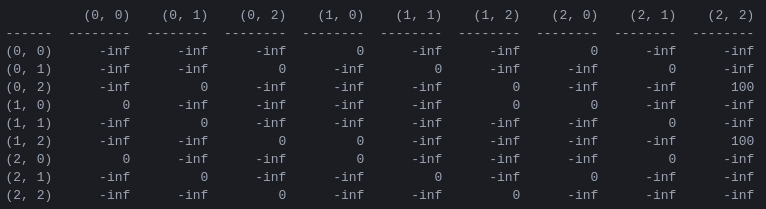
图 4. N = 2圆盘的汉诺塔谜题的奖励矩阵R第 ( i , j ) 个元素表示从状态i移动到j的奖励。状态由元组标记,如图 2 和图 3 所示,不同之处在于,钉子以“Python 方式”索引,从 0 到 2,而不是从 1 到 3。导致目标状态 (2,2) 的移动会被分配奖励为 100,非法走法为 ,所有其他走法为 0。
奖励矩阵R仅描述即时奖励:只有从倒数第二个状态 (0,2) 和 (1,2) 才能获得 100 的奖励。在其他状态中,2 或 3 种可能的移动中的每一种都有相同的奖励 0,并且没有明显的理由选择其中一种。
最终,我们寻求为每个状态中的每个可能的移动分配一个“值”,以便通过最大化这些值,我们可以定义导致最佳解决方案的策略。每个状态下每个动作的“值”矩阵称为Q ,可以按照 Watkins 和 Dayan [1] 所描述的随机方式递归求解或“学习”。 2 个磁盘的结果如图 5 所示。
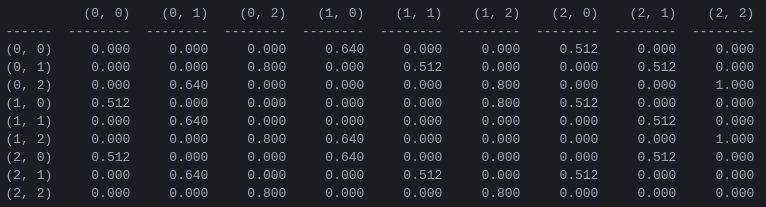
图 5.具有 2 个圆盘的汉诺塔游戏的“动作值”矩阵Q ,以折扣因子 = 0.8、学习因子 = 1.0 和 1000 个训练集进行学习。
矩阵Q的值本质上是可以分配给图 3 中状态转换图的顶点的权重,它引导智能体以尽可能短的方式从初始状态到目标状态。在此示例中,通过从状态 (0,0) 开始并连续选择具有最高Q值的移动,读者可以确信Q矩阵引导智能体通过状态序列 (0,0) - (1 ,0) - (1,2) - (2,2),对应于 2 盘汉诺塔游戏的 3 步最优解(图 6)。
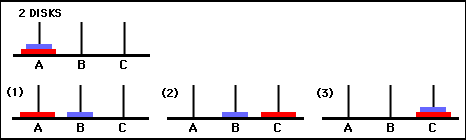
图 6.使用 2 个圆盘的汉诺塔游戏的解决方案。连续状态分别由(0,0)、(1,0)、(1,2)和(2,2)表示。 (来源:mathforum.org)。
在此示例中,矩阵Q已收敛到其最优值,它定义了一个固定策略:每一行包含一个具有唯一最大值的操作。然而,在学习过程中,不同的动作可能具有相同的Q值。 (特别是,当Q初始化为零矩阵时,就是训练开始时的情况)。在下一节介绍的模拟中,此类情况通过以下随机策略处理:在多个操作之间共享最大 Q 值的情况下,随机选择这些操作之一。
Q 学习算法的性能可以通过计算解决汉诺塔难题所需的(平均)移动次数来衡量。该数字随着训练次数的增加而减少,直到最终达到最佳值 2 N - 1,其中N是磁盘数量,如图 7 所示,其中N = 2、3 和 4。
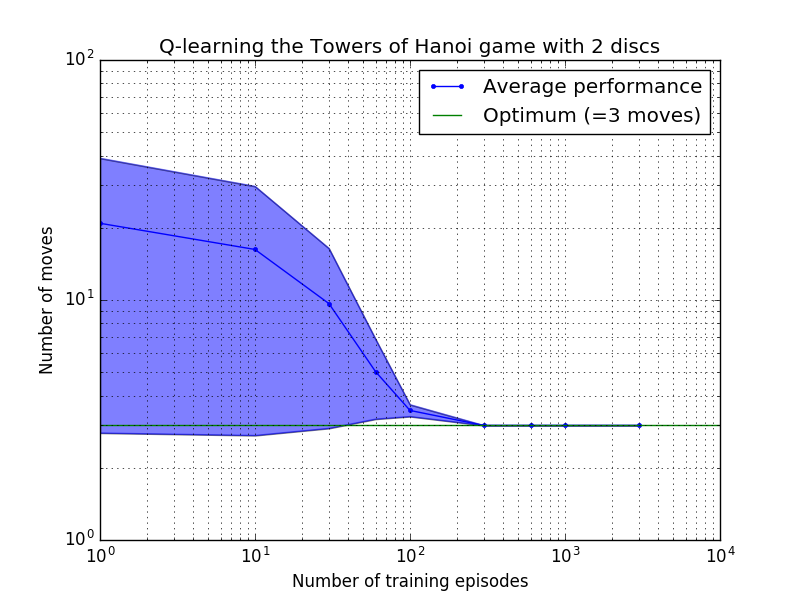
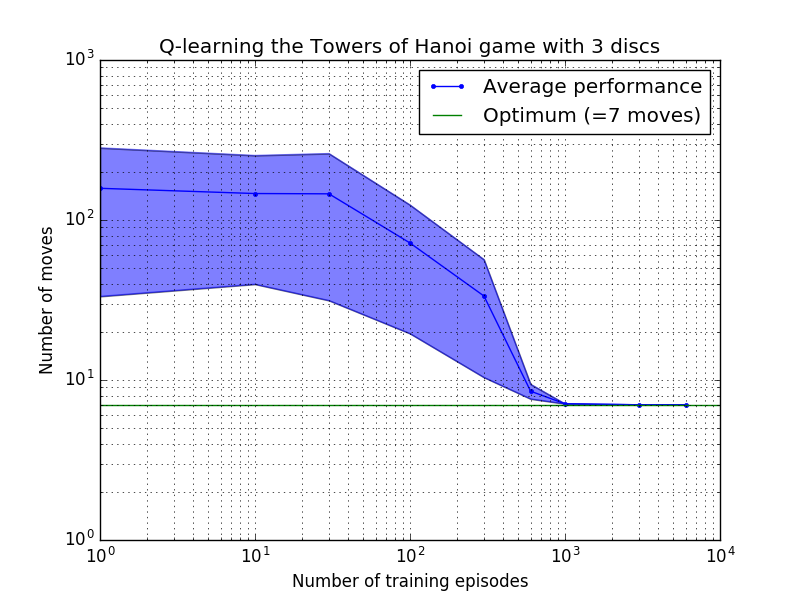
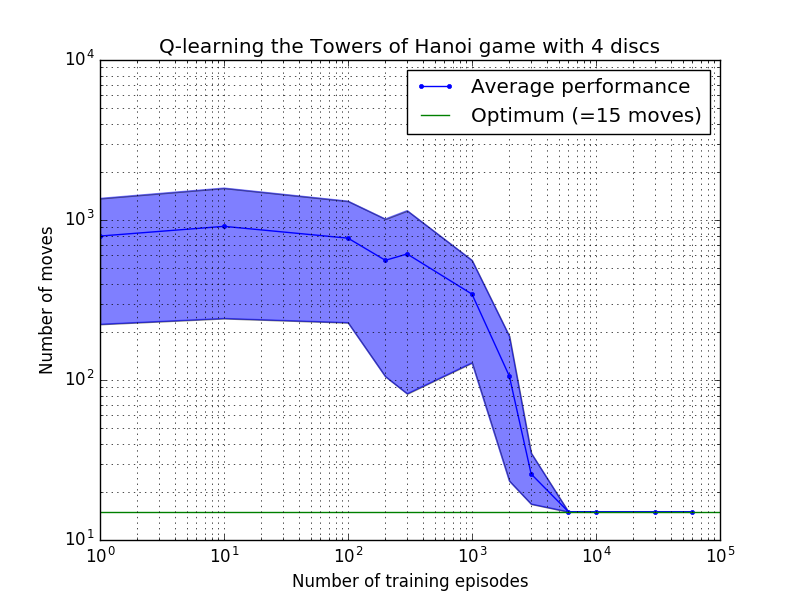
图 7.汉诺塔游戏的 Q 学习算法的性能(从上到下依次为 2、3 和 4 个磁盘)。在所有情况下,学习都是以= 0.8 的折扣因子和= 1.0 的学习因子进行的。蓝色实线代表每个生成的随机策略经过 100 个 epoch 训练和玩 100 次游戏后的平均性能。蓝色阴影区域的上限和下限与平均值的偏移量是估计的标准差。 (对于N = 3 和N = 4,由于计算限制,训练次数和播放次数分别减少到 10 和 10)。
图 7 中学习特性的一个有趣特征是,在所有情况下,学习最初都很慢,并且智能体很难比随机选择动作的“零训练”策略做得更好。在某个时刻,学习达到“拐点”,然后以加速的速度收敛到最佳移动次数(尽管这在对数尺度上有些夸大)。
Python 脚本通过 Q 学习成功地针对任意数量的磁盘成功解决了河内塔难题。该脚本可以轻松适应具有不同奖励矩阵R其他问题。
收敛到最佳解决方案所需的训练次数随着磁盘数量N增加而大大增加:对于N=2磁盘,需要约 300 次训练,而对于N=4则需要约 6,000 次训练。学习算法的一个可能的改进是允许它自动寻找递归解决方案,正如 Hengst [3] 所做的那样。
[1] Watkins & Dayan, Q-learning ,机器学习,8, 279-292 (1992)。 (PDF)。
[2] Anderson,多层连接系统的学习和问题解决,博士。论文(1986)。 (PDF)。
[3] Hengst,用 HEXQ 发现强化学习的层次结构,第十九届国际机器学习会议论文集(2002 年)。 (PDF)。