alphafold2

Alphafold2 - Pytorch（正在开发中）

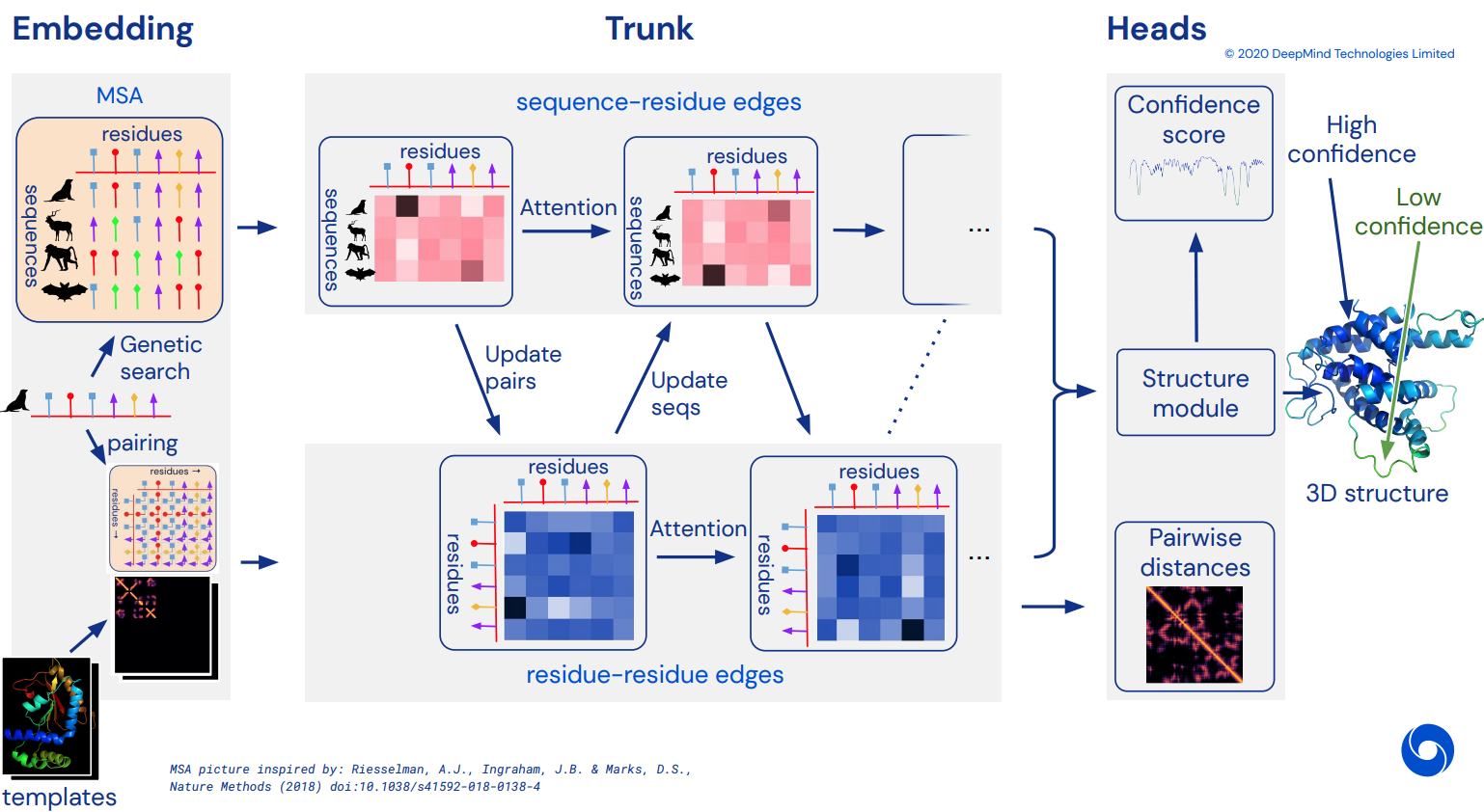
最终成为 Alphafold2 的非官方工作 Pytorch 实现，Alphafold2 是解决 CASP14 问题的令人惊叹的注意力网络。随着更多架构细节的发布，将逐步实现。

一旦复制完成，我打算在计算机中折叠所有可用的氨基酸序列，并将其作为学术洪流发布，以进一步促进科学发展。如果您对复制工作感兴趣，请访问此 Discord 频道的 #alphafold

更新：Deepmind 开源了 Jax 中的官方代码以及权重！该存储库现在将面向直接 pytorch 翻译，并对位置编码进行一些改进

ArxivInsights 视频

安装

$ pip install alphafold2-pytorch

地位

lhatsk 已报告使用与 trRosetta 相同的设置来训练该存储库的修改后的主干，并取得了有竞争力的结果

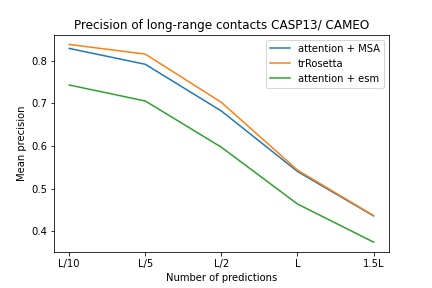
blue used the the trRosetta input (MSA -> potts -> axial attention), green used the ESM embedding (only sequence) -> tiling -> axial attention - lhatsk

用法

预测直方图，类似于 Alphafold-1，但需要注意

 import torch
from alphafold2_pytorch import Alphafold2

model = Alphafold2 (
    dim = 256 ,
    depth = 2 ,
    heads = 8 ,
    dim_head = 64 ,
    reversible = False  # set this to True for fully reversible self / cross attention for the trunk
). cuda ()

seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()      # AA length of 128
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()   # MSA doesn't have to be the same length as primary sequence
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()

distogram = model (
    seq ,
    msa ,
    mask = mask ,
    msa_mask = msa_mask
) # (1, 128, 128, 37)

您还可以通过在 init 上传递predict_angles = True来打开角度预测。下面的例子相当于 trRosetta 但具有自我/交叉注意力。

 import torch
from alphafold2_pytorch import Alphafold2

model = Alphafold2 (
    dim = 256 ,
    depth = 2 ,
    heads = 8 ,
    dim_head = 64 ,
    predict_angles = True   # set this to True
). cuda ()

seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()

distogram , theta , phi , omega = model (
    seq ,
    msa ,
    mask = mask ,
    msa_mask = msa_mask
)

# distogram - (1, 128, 128, 37),
# theta     - (1, 128, 128, 25),
# phi       - (1, 128, 128, 13),
# omega     - (1, 128, 128, 25) 

预测坐标

Fabian 最近的论文建议将坐标迭代反馈回 SE3 Transformer，共享权重，可能会起作用。我决定根据这个想法来执行，尽管它的实际运作方式仍然悬而未决。

您还可以使用 E(n)-Transformer 或 EGNN 进行结构细化。

更新：Baker 的实验室已经证明，从序列和 MSA 嵌入到 SE3 Transformer 的端到端架构可以最好地超越 trRosetta，并缩小与 Alphafold2 的差距。我们将使用作用于主干嵌入的图形转换器来生成要发送到等变网络的初始坐标集。 （Costa 等人在 Baker 实验室发表之前的一篇论文中从 MSA Transformer 嵌入中梳理出 3D 坐标，进一步证实了这一点）

 import torch
from alphafold2_pytorch import Alphafold2

model = Alphafold2 (
    dim = 256 ,
    depth = 2 ,
    heads = 8 ,
    dim_head = 64 ,
    predict_coords = True ,
    structure_module_type = 'se3' ,          # use SE3 Transformer - if set to False, will use E(n)-Transformer, Victor and Max Welling's new paper
    structure_module_dim = 4 ,               # se3 transformer dimension
    structure_module_depth = 1 ,             # depth
    structure_module_heads = 1 ,             # heads
    structure_module_dim_head = 16 ,         # dimension of heads
    structure_module_refinement_iters = 2 ,  # number of equivariant coordinate refinement iterations
    structure_num_global_nodes = 1          # number of global nodes for the structure module, only works with SE3 transformer
). cuda ()

seq = torch . randint ( 0 , 21 , ( 2 , 64 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 2 , 5 , 60 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()

coords = model (
    seq ,
    msa ,
    mask = mask ,
    msa_mask = msa_mask
) # (2, 64 * 3, 3)  <-- 3 atoms per residue 

原子

基本假设是主干在残差级别上工作，然后构成结构模块的原子级别，无论是 SE3 Transformers、E(n)-Transformer 还是 EGNN 进行细化。该库默认使用 3 个主链原子（C、Ca、N），但您可以将其配置为包含您喜欢的任何其他原子，包括 Cb 和侧链。

 import torch
from alphafold2_pytorch import Alphafold2

model = Alphafold2 (
    dim = 256 ,
    depth = 2 ,
    heads = 8 ,
    dim_head = 64 ,
    predict_coords = True ,
    atoms = 'backbone-with-cbeta'
). cuda ()

seq = torch . randint ( 0 , 21 , ( 2 , 64 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 2 , 5 , 60 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()

coords = model (
    seq ,
    msa ,
    mask = mask ,
    msa_mask = msa_mask
) # (2, 64 * 4, 3)  <-- 4 atoms per residue (C, Ca, N, Cb)

atoms的有效选择包括：

• backbone - 3 个主链原子（C、Ca、N）[默认]
• backbone-with-cbeta - 3 个骨干原子和 C beta
• backbone-with-oxygen - 3 个主链原子和来自羧基的氧
• backbone-with-cbeta-and-oxygen - 3 个具有 Cβ 和氧的主链原子
• all - 主链和侧链的所有其他原子

您还可以传入形状为 (14,) 的张量，定义您想要包含哪些原子

前任。

 atoms = torch . tensor ([ 1 , 1 , 1 , 1 , 1 , 1 , 0 , 1 , 0 , 0 , 0 , 0 , 0 , 1 ])

MSA、ESM 或 ProtTrans 嵌入

该存储库为您提供了通过 Facebook AI 预先训练的嵌入来轻松补充网络的方法。它包含预训练的 ESM、MSA Transformer 或 Protein Transformer 的包装。

有一些先决条件。您需要确保安装了 Nvidia 的 apex 库，因为预训练的 Transformer 使用一些融合操作。

或者您可以尝试运行下面的脚本

git clone https://github.com/NVIDIA/apex
cd apex
pip install -v --disable-pip-version-check --no-cache-dir --global-option= " --cpp_ext " --global-option= " --cuda_ext " ./

接下来，您只需使用ESMEmbedWrapper 、 MSAEmbedWrapper或ProtTranEmbedWrapper导入并包装您的Alphafold2实例，它将负责为您嵌入序列和多序列比对（并将其投影到您的模型）。除了添加包装器之外，不需要进行任何更改。

 import torch
from alphafold2_pytorch import Alphafold2
from alphafold2_pytorch . embeds import MSAEmbedWrapper

alphafold2 = Alphafold2 (
    dim = 256 ,
    depth = 2 ,
    heads = 8 ,
    dim_head = 64
)

model = MSAEmbedWrapper (
    alphafold2 = alphafold2
). cuda ()

seq = torch . randint ( 0 , 21 , ( 2 , 16 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()

msa = torch . randint ( 0 , 21 , ( 2 , 5 , 16 )). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()

distogram = model (
    seq ,
    msa ,
    mask = mask ,
    msa_mask = msa_mask
)

默认情况下，即使包装器向主干提供序列和 MSA 嵌入，它们也会与通常的令牌嵌入相加。如果您想在没有令牌嵌入的情况下训练 Alphafold2（仅依赖于预训练的嵌入），则需要在Alphafold2初始化时将disable_token_embed设置为True 。

 alphafold2 = Alphafold2 (
    dim = 256 ,
    depth = 2 ,
    heads = 8 ,
    dim_head = 64 ,
    disable_token_embed = True
)

实值距离预测

Jinbo Xu 的一篇论文表明，不需要对距离进行分类，而是可以直接预测平均值和标准差。您可以通过打开一个标志predict_real_value_distances来使用此功能，在这种情况下，返回的距离预测的平均值和标准差的维度将分别为2 。

如果predict_coords也打开，则 MDS 将直接接受平均值和标准差预测，而无需从分布图箱中进行计算。

 import torch
from alphafold2_pytorch import Alphafold2

model = Alphafold2 (
    dim = 256 ,
    depth = 2 ,
    heads = 8 ,
    dim_head = 64 ,
    predict_coords = True ,
    predict_real_value_distances = True ,      # set this to True
    structure_module_type = 'se3' ,
    structure_module_dim = 4 ,
    structure_module_depth = 1 ,
    structure_module_heads = 1 ,
    structure_module_dim_head = 16 ,
    structure_module_refinement_iters = 2
). cuda ()

seq = torch . randint ( 0 , 21 , ( 2 , 64 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 2 , 5 , 60 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()

coords = model (
    seq ,
    msa ,
    mask = mask ,
    msa_mask = msa_mask
) # (2, 64 * 3, 3)  <-- 3 atoms per residue 

卷积

您可以为主序列和 MSA 添加卷积块，只需设置一个额外的关键字参数use_conv = True

 import torch
from alphafold2_pytorch import Alphafold2

model = Alphafold2 (
    dim = 256 ,
    depth = 2 ,
    heads = 8 ,
    dim_head = 64 ,
    use_conv = True # set this to True
). cuda ()

seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()

distogram = model (
    seq ,
    msa ,
    mask = mask ,
    msa_mask = msa_mask
) # (1, 128, 128, 37)

卷积核遵循本文的思路，将 1d 和 2d 核组合在一个类似 resnet 的块中。您可以完全自定义内核。

 import torch
from alphafold2_pytorch import Alphafold2

model = Alphafold2 (
    dim = 256 ,
    depth = 2 ,
    heads = 8 ,
    dim_head = 64 ,
    use_conv = True , # set this to True
    conv_seq_kernels = (( 9 , 1 ), ( 1 , 9 ), ( 3 , 3 )), # kernels for N x N primary sequence
    conv_msa_kernels = (( 1 , 9 ), ( 3 , 3 )), # kernels for {num MSAs} x N MSAs
). cuda ()

seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()

distogram = model (
    seq ,
    msa ,
    mask = mask ,
    msa_mask = msa_mask
) # (1, 128, 128, 37)

您还可以使用一个额外的关键字参数进行循环扩张。所有层的默认膨胀均为1 。

 import torch
from alphafold2_pytorch import Alphafold2

model = Alphafold2 (
    dim = 256 ,
    depth = 2 ,
    heads = 8 ,
    dim_head = 64 ,
    use_conv = True , # set this to True
    dilations = ( 1 , 3 , 5 ) # cycle between dilations of 1, 3, 5
). cuda ()

seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()

distogram = model (
    seq ,
    msa ,
    mask = mask ,
    msa_mask = msa_mask
) # (1, 128, 128, 37)

最后，您可以使用custom_block_types关键字自定义您想要的任何顺序，而不是遵循卷积、自注意力、每个深度重复的交叉注意力的模式

前任。首先主要进行卷积，然后是自注意力 + 交叉注意力块的网络

 import torch
from alphafold2_pytorch import Alphafold2

model = Alphafold2 (
    dim = 256 ,
    heads = 8 ,
    dim_head = 64 ,
    custom_block_types = (
        * (( 'conv' ,) * 6 ),
        * (( 'self' , 'cross' ) * 6 )
    )
). cuda ()

seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()

distogram = model (
    seq ,
    msa ,
    mask = mask ,
    msa_mask = msa_mask
) # (1, 128, 128, 37) 

稀疏注意力

您可以使用 Microsoft Deepspeed 的 Sparse Attention 进行训练，但您必须忍受安装过程。这是两步。

首先，需要安装 Deepspeed with Sparse Attention

$ sh install_deepspeed.sh

接下来，您需要安装 pip 包triton

$ pip install triton

如果上述两项都成功，那么现在您可以使用稀疏注意力进行训练！

遗憾的是，稀疏注意力仅支持自注意力，而不支持交叉注意力。我将引入一个不同的解决方案来提高交叉注意力的性能。

 model = Alphafold2 (
    dim = 256 ,
    depth = 12 ,
    heads = 8 ,
    dim_head = 64 ,
    max_seq_len = 2048 ,                   # the maximum sequence length, this is required for sparse attention. the input cannot exceed what is set here
    sparse_self_attn = ( True , False ) * 6  # interleave sparse and full attention for all 12 layers
). cuda ()

线性注意力

我还添加了最好的线性注意力变体之一，希望减轻交叉注意力的负担。我个人还没有发现 Performer 工作得那么好，但由于他们在论文中报告了一些蛋白质基准的不错的数字，我想我应该包括它并允许其他人进行实验。

 import torch
from alphafold2_pytorch import Alphafold2

model = Alphafold2 (
    dim = 256 ,
    depth = 2 ,
    heads = 8 ,
    dim_head = 64 ,
    cross_attn_linear = True # simply set this to True to use Performer for all cross attention
). cuda ()

您还可以通过传入与深度相同长度的元组来指定您希望使用线性注意力的确切层

 import torch
from alphafold2_pytorch import Alphafold2

model = Alphafold2 (
    dim = 256 ,
    depth = 6 ,
    heads = 8 ,
    dim_head = 64 ,
    cross_attn_linear = ( True , False ) * 3 # interleave linear and full attention
). cuda ()

交叉注意力的克罗内克注意力

本文建议，如果您有定义轴的查询或上下文（例如一张图像），您可以通过对这些轴（高度和宽度）进行平均并将平均轴连接成一个序列来减少所需的注意力。您可以将其打开作为交叉注意的内存节省技术，特别是对于主序列。

 import torch
from alphafold2_pytorch import Alphafold2

model = Alphafold2 (
    dim = 256 ,
    depth = 6 ,
    heads = 8 ,
    dim_head = 64 ,
    cross_attn_kron_primary = True # make sure primary sequence undergoes the kronecker operator during cross attention
). cuda ()

如果您的 MSA 对齐并且宽度相同，您还可以在交叉关注期间使用cross_attn_kron_msa标志将相同的运算符应用于 MSA。

托多

• 提供掩蔽均值缩减法
• 旋转嵌入

记忆压缩注意力

为了节省交叉注意力的内存，您可以按照本文中列出的方案设置键/值的压缩比。 2-4 的压缩比通常是可以接受的。

 model = Alphafold2 (
    dim = 256 ,
    depth = 12 ,
    heads = 8 ,
    dim_head = 64 ,
    cross_attn_compress_ratio = 3
). cuda ()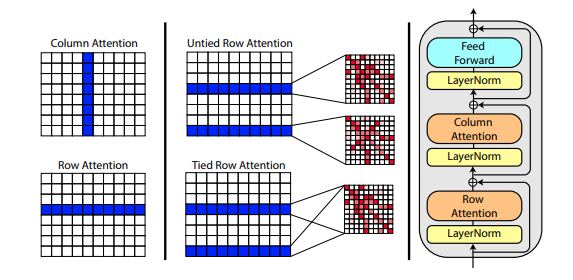

Trunk 中的 MSA 处理

Roshan Rao 的一篇新论文提出使用轴向注意力对 MSA 进行预训练。鉴于强劲的结果，该存储库将在主干中使用相同的方案，专门用于 MSA 自注意力。

您还可以在初始化Alphafold2时将 MSA 的行注意力与msa_tie_row_attn = True设置联系起来。但是，为了使用此功能，您必须确保如果每个主序列的 MSA 数量不均匀，则对于未使用的行，MSA 掩码已正确设置为False 。

 model = Alphafold2 (
    dim = 256 ,
    depth = 2 ,
    heads = 8 ,
    dim_head = 64 ,
    msa_tie_row_attn = True # just set this to true
)

Trunk中的模板处理

模板处理也主要通过轴向注意力完成，交叉注意力沿着模板维度的数量完成。这很大程度上遵循与最近的全注意力视频分类方法相同的方案，如此处所示。

 import torch
from alphafold2_pytorch import Alphafold2

model = Alphafold2 (
    dim = 256 ,
    depth = 5 ,
    heads = 8 ,
    dim_head = 64 ,
    reversible = True ,
    sparse_self_attn = False ,
    max_seq_len = 256 ,
    cross_attn_compress_ratio = 3
). cuda ()

seq = torch . randint ( 0 , 21 , ( 1 , 16 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()

msa = torch . randint ( 0 , 21 , ( 1 , 10 , 16 )). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()

templates_seq = torch . randint ( 0 , 21 , ( 1 , 2 , 16 )). cuda ()
templates_coors = torch . randint ( 0 , 37 , ( 1 , 2 , 16 , 3 )). cuda ()
templates_mask = torch . ones_like ( templates_seq ). bool (). cuda ()

distogram = model (
    seq ,
    msa ,
    mask = mask ,
    msa_mask = msa_mask ,
    templates_seq = templates_seq ,
    templates_coors = templates_coors ,
    templates_mask = templates_mask
)

如果侧链信息也存在，以每个残基的 C 和 C-alpha 坐标之间的单位向量的形式存在，您也可以按如下方式传递它。

 import torch
from alphafold2_pytorch import Alphafold2

model = Alphafold2 (
    dim = 256 ,
    depth = 5 ,
    heads = 8 ,
    dim_head = 64 ,
    reversible = True ,
    sparse_self_attn = False ,
    max_seq_len = 256 ,
    cross_attn_compress_ratio = 3
). cuda ()

seq = torch . randint ( 0 , 21 , ( 1 , 16 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()

msa = torch . randint ( 0 , 21 , ( 1 , 10 , 16 )). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()

templates_seq = torch . randint ( 0 , 21 , ( 1 , 2 , 16 )). cuda ()
templates_coors = torch . randn ( 1 , 2 , 16 , 3 ). cuda ()
templates_mask = torch . ones_like ( templates_seq ). bool (). cuda ()

templates_sidechains = torch . randn ( 1 , 2 , 16 , 3 ). cuda () # unit vectors of difference of C and C-alpha coordinates

distogram = model (
    seq ,
    msa ,
    mask = mask ,
    msa_mask = msa_mask ,
    templates_seq = templates_seq ,
    templates_mask = templates_mask ,
    templates_coors = templates_coors ,
    templates_sidechains = templates_sidechains
)

等变注意力

我已经准备好了 SE3 Transformer 的重新实现，正如 Fabian Fuchs 在一篇推测性博客文章中所解释的那样。

此外，Victor 和 Welling 的一篇新论文使用 E(n) 等方差的不变特征，在许多基准测试中达到了 SOTA 并优于 SE3 Transformer，同时速度更快。我采用了本文的主要思想，并将其修改为变压器（增加了对功能和坐标更新的关注）。

上述所有三个等变网络均已集成，只需设置一个超参数structure_module_type即可在存储库中使用以进行原子坐标细化。

• se3 SE3 变压器

• egnn

• en E(n)-变压器

引起读者兴趣的是，这三个框架中的每一个都已经过研究人员对相关问题的验证。

测试

$ python setup.py test 

数据

该库将使用 Jonathan King 在此存储库中的出色工作。谢谢乔纳森！

我们还有 MSA 数据，全部价值约 3.5 TB，由拥有 The-Eye 项目的档案管理员下载和托管。 （他们还托管 Eleuther AI 的数据和模型）如果您发现它们有帮助，请考虑捐赠。

$ curl -s https://the-eye.eu/eleuther_staging/globus_stuffs/tree.txt

投机

https://xukui.cn/alphafold2.html

https://moalquraishi.wordpress.com/2020/12/08/alphafold2-casp14-it-feels-like-ones-child-has-left-home/

竞争实验室的最新作品

https://www.biorxiv.org/content/10.1101/2020.12.10.419994v1.full.pdf

https://pubmed.ncbi.nlm.nih.gov/33637700/

tFold 演示，来自腾讯 AI 实验室

外部封装

• 最后一步- 快速放松 -安装说明：
  • 从以下位置下载 Pyrosetta 轮：http://www.pyrosetta.org/dow（选择适当的版本） - 请注意该文件很重（约 1.2 Gb）
    • 任何拥有学术电子邮件的人都应该免费下载
  • Bash > cd downloads_folder > pip install pyrosetta_wheel_filename.whl

OpenMM 琥珀色

引文

 @misc { unpublished2021alphafold2 ,
    title   = { Alphafold2 } ,
    author  = { John Jumper } ,
    year    = { 2020 } ,
    archivePrefix = { arXiv } ,
    primaryClass = { q-bio.BM }
}

 @article { Rao2021.02.12.430858 ,
    author  = { Rao, Roshan and Liu, Jason and Verkuil, Robert and Meier, Joshua and Canny, John F. and Abbeel, Pieter and Sercu, Tom and Rives, Alexander } ,
    title   = { MSA Transformer } ,
    year    = { 2021 } ,
    publisher = { Cold Spring Harbor Laboratory } ,
    URL     = { https://www.biorxiv.org/content/early/2021/02/13/2021.02.12.430858 } ,
    journal = { bioRxiv }
}

 @article { Rives622803 ,
    author  = { Rives, Alexander and Goyal, Siddharth and Meier, Joshua and Guo, Demi and Ott, Myle and Zitnick, C. Lawrence and Ma, Jerry and Fergus, Rob } ,
    title   = { Biological Structure and Function Emerge from Scaling Unsupervised Learning to 250 Million Protein Sequences } ,
    year    = { 2019 } ,
    doi     = { 10.1101/622803 } ,
    publisher = { Cold Spring Harbor Laboratory } ,
    journal = { bioRxiv }
}

 @article { Elnaggar2020.07.12.199554 ,
    author  = { Elnaggar, Ahmed and Heinzinger, Michael and Dallago, Christian and Rehawi, Ghalia and Wang, Yu and Jones, Llion and Gibbs, Tom and Feher, Tamas and Angerer, Christoph and Steinegger, Martin and BHOWMIK, DEBSINDHU and Rost, Burkhard } ,
    title   = { ProtTrans: Towards Cracking the Language of Life{textquoteright}s Code Through Self-Supervised Deep Learning and High Performance Computing } ,
    elocation-id = { 2020.07.12.199554 } ,
    year    = { 2021 } ,
    doi     = { 10.1101/2020.07.12.199554 } ,
    publisher = { Cold Spring Harbor Laboratory } ,
    URL     = { https://www.biorxiv.org/content/early/2021/05/04/2020.07.12.199554 } ,
    eprint  = { https://www.biorxiv.org/content/early/2021/05/04/2020.07.12.199554.full.pdf } ,
    journal = { bioRxiv }
}

 @misc { king2020sidechainnet ,
    title   = { SidechainNet: An All-Atom Protein Structure Dataset for Machine Learning } , 
    author  = { Jonathan E. King and David Ryan Koes } ,
    year    = { 2020 } ,
    eprint  = { 2010.08162 } ,
    archivePrefix = { arXiv } ,
    primaryClass = { q-bio.BM }
}

 @misc { alquraishi2019proteinnet ,
    title   = { ProteinNet: a standardized data set for machine learning of protein structure } , 
    author  = { Mohammed AlQuraishi } ,
    year    = { 2019 } ,
    eprint  = { 1902.00249 } ,
    archivePrefix = { arXiv } ,
    primaryClass = { q-bio.BM }
}

 @misc { gomez2017reversible ,
    title     = { The Reversible Residual Network: Backpropagation Without Storing Activations } , 
    author    = { Aidan N. Gomez and Mengye Ren and Raquel Urtasun and Roger B. Grosse } ,
    year      = { 2017 } ,
    eprint    = { 1707.04585 } ,
    archivePrefix = { arXiv } ,
    primaryClass = { cs.CV }
}

 @misc { fuchs2021iterative ,
    title   = { Iterative SE(3)-Transformers } ,
    author  = { Fabian B. Fuchs and Edward Wagstaff and Justas Dauparas and Ingmar Posner } ,
    year    = { 2021 } ,
    eprint  = { 2102.13419 } ,
    archivePrefix = { arXiv } ,
    primaryClass = { cs.LG }
}

 @misc { satorras2021en ,
    title   = { E(n) Equivariant Graph Neural Networks } , 
    author  = { Victor Garcia Satorras and Emiel Hoogeboom and Max Welling } ,
    year    = { 2021 } ,
    eprint  = { 2102.09844 } ,
    archivePrefix = { arXiv } ,
    primaryClass = { cs.LG }
}

 @misc { su2021roformer ,
    title   = { RoFormer: Enhanced Transformer with Rotary Position Embedding } ,
    author  = { Jianlin Su and Yu Lu and Shengfeng Pan and Bo Wen and Yunfeng Liu } ,
    year    = { 2021 } ,
    eprint  = { 2104.09864 } ,
    archivePrefix = { arXiv } ,
    primaryClass = { cs.CL }
}

 @article { Gao_2020 ,
    title   = { Kronecker Attention Networks } ,
    ISBN    = { 9781450379984 } ,
    url     = { http://dx.doi.org/10.1145/3394486.3403065 } ,
    DOI     = { 10.1145/3394486.3403065 } ,
    journal = { Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining } ,
    publisher = { ACM } ,
    author  = { Gao, Hongyang and Wang, Zhengyang and Ji, Shuiwang } ,
    year    = { 2020 } ,
    month   = { Jul }
}

 @article { Si2021.05.10.443415 ,
    author  = { Si, Yunda and Yan, Chengfei } ,
    title   = { Improved protein contact prediction using dimensional hybrid residual networks and singularity enhanced loss function } ,
    elocation-id = { 2021.05.10.443415 } ,
    year    = { 2021 } ,
    doi     = { 10.1101/2021.05.10.443415 } ,
    publisher = { Cold Spring Harbor Laboratory } ,
    URL     = { https://www.biorxiv.org/content/early/2021/05/11/2021.05.10.443415 } ,
    eprint  = { https://www.biorxiv.org/content/early/2021/05/11/2021.05.10.443415.full.pdf } ,
    journal = { bioRxiv }
}

 @article { Costa2021.06.02.446809 ,
    author  = { Costa, Allan and Ponnapati, Manvitha and Jacobson, Joseph M. and Chatterjee, Pranam } ,
    title   = { Distillation of MSA Embeddings to Folded Protein Structures with Graph Transformers } ,
    year    = { 2021 } ,
    doi     = { 10.1101/2021.06.02.446809 } ,
    publisher = { Cold Spring Harbor Laboratory } ,
    URL     = { https://www.biorxiv.org/content/early/2021/06/02/2021.06.02.446809 } ,
    eprint  = { https://www.biorxiv.org/content/early/2021/06/02/2021.06.02.446809.full.pdf } ,
    journal = { bioRxiv }
}

 @article { Baek2021.06.14.448402 ,
    author  = { Baek, Minkyung and DiMaio, Frank and Anishchenko, Ivan and Dauparas, Justas and Ovchinnikov, Sergey and Lee, Gyu Rie and Wang, Jue and Cong, Qian and Kinch, Lisa N. and Schaeffer, R. Dustin and Mill{'a}n, Claudia and Park, Hahnbeom and Adams, Carson and Glassman, Caleb R. and DeGiovanni, Andy and Pereira, Jose H. and Rodrigues, Andria V. and van Dijk, Alberdina A. and Ebrecht, Ana C. and Opperman, Diederik J. and Sagmeister, Theo and Buhlheller, Christoph and Pavkov-Keller, Tea and Rathinaswamy, Manoj K and Dalwadi, Udit and Yip, Calvin K and Burke, John E and Garcia, K. Christopher and Grishin, Nick V. and Adams, Paul D. and Read, Randy J. and Baker, David } ,
    title   = { Accurate prediction of protein structures and interactions using a 3-track network } ,
    year    = { 2021 } ,
    doi     = { 10.1101/2021.06.14.448402 } ,
    publisher = { Cold Spring Harbor Laboratory } ,
    URL     = { https://www.biorxiv.org/content/early/2021/06/15/2021.06.14.448402 } ,
    eprint  = { https://www.biorxiv.org/content/early/2021/06/15/2021.06.14.448402.full.pdf } ,
    journal = { bioRxiv }
}