ai simplest network

最简单的人工神经网络

这是可能解释和演示的最简单的人工神经网络。

这是关于神经网络的 github 存储库系列的第 1 部分

• 第 1 部分 - 最简单的网络（你在这里）
• 第 2 部分 - 反向传播
• 第 3 部分 - 反向传播（续）

目录

• 理论
  • 模仿神经元
  • 一个简单的例子
  • 错误
  • 梯度下降
• 代码示例
• 参考

理论

模仿神经元

人工神经网络受到大脑的启发，通过互连的人工神经元存储模式并相互通信。最简单形式的人工神经元有一个或多个输入每个都有特定的重量和一个输出 。

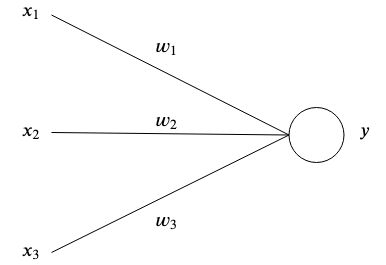
在最简单的层面上，输出是输入的总和乘以权重。

一个简单的例子

网络的目的是学习特定的输出给定某些输入通过近似具有许多参数的复杂函数我们无法自己想出办法。

假设我们有一个有两个输入的网络和和两个重量和 。

这个想法是调整权重，使给定的输入产生所需的输出。

权重通常是随机初始化的，因为我们无法提前知道它们的最佳值，但是为了简单起见，我们将它们都初始化为 。

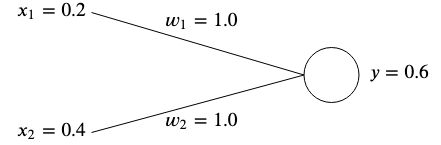
如果我们计算该网络的输出，我们将得到

错误

如果输出与预期的目标值不匹配，那么我们就会出错。
例如，如果我们想要获得目标值那么我们会有差异

测量误差（也称为成本函数）的一种常见方法是使用均方误差：

如果我们有输入和目标值的多个关联，那么误差就变成每个关联的平均和。

我们使用均方误差来衡量结果与我们期望目标的距离。平方消除了负号，并为输出和目标之间的较大差异赋予更多权重。

为了纠正错误，我们需要调整权重，使输出与我们的目标相匹配。在我们的示例中，降低从到会成功的，因为

然而，为了针对许多不同的输入和目标值调整神经网络的权重，我们需要一种学习算法来自动为我们做到这一点。

梯度下降

这个想法是使用误差来理解应该如何调整每个权重以使误差最小化，但首先，我们需要了解梯度。

什么是梯度？

它本质上是一个指向函数最陡上升方向的向量。梯度表示为是表示为向量的函数的每个变量的偏导数。

对于两个变量函数来说，它看起来像这样：

让我们注入一些数字并用一个简单的例子来计算梯度。假设我们有一个函数 ，那么梯度就是

什么是梯度下降？

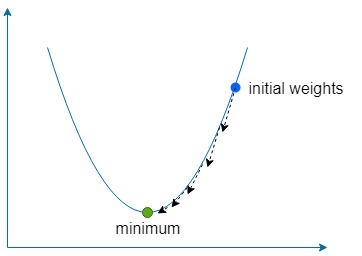
下降部分简单地意味着使用梯度来找到函数最陡上升的方向，然后沿相反方向多次移动以找到函数全局（有时是局部）最小值。

我们使用一个称为学习率的常数，表示为定义朝这个方向迈出多小的一步。

如果太大，那么我们就有超过函数最小值的风险，但如果太低，那么网络将需要更长的时间来学习，并且我们有陷入浅局部最小值的风险。

梯度下降应用于我们的示例网络

对于我们的两个权重和我们需要找到这些权重相对于误差函数的梯度

对于两者和 ，我们可以利用链式法则求梯度

从现在开始我们将表示作为简单的术语。

一旦我们有了梯度，我们就可以通过减去计算出的梯度乘以学习率来更新权重。

我们重复这个过程，直到误差最小化并且足够接近于零。

代码示例

包含的示例使用梯度下降向具有两个输入和一个输出的神经网络教授以下数据集：

一旦学习到，当给定两个时，网络应该输出〜0 和〜 当给定一个和一个 。

如何跑

在 repl.it 上在线

码头工人

docker build -t simplest-network .
docker run --rm simplest-network

参考

1. 人工智能引擎，作者：James V Stone (2019)
2. 深度学习完整指南：http://neuralnetworksanddeeplearning.com/chap2.html