nano neuron

纳米神经元

7 个简单的 JavaScript 函数将让您了解机器如何真正“学习”。

其他语言：Русский、Português

您可能还感兴趣？交互式机器学习实验

长话短说

NanoNeuron 是神经网络中神经元概念的过度简化版本。 NanoNeuron 经过训练，可以将温度值从摄氏度转换为华氏度。

NanoNeuron.js 代码示例包含 7 个简单的 JavaScript 函数（涉及模型预测、成本计算、前向/后向传播和训练），让您了解机器如何实际“学习”。没有第三方库，没有外部数据集或依赖项，只有纯粹而简单的 JavaScript 函数。

☝？无论如何，这些函数都不是机器学习的完整指南。许多机器学习概念被跳过并过度简化！这种简化的目的是让读者对机器如何学习有一个真正基本的理解和感受，并最终让读者认识到这不是“机器学习魔法”，而是“机器学习数学”？

我们的 NanoNeuron 将学到什么

您可能听说过神经网络背景下的神经元。 NanoNeuron 就是这样，但更简单，我们将从头开始实现它。出于简单原因，我们甚至不打算在 NanoNeurons 上构建网络。我们会让这一切自行运作，为我们做出一些神奇的预测。也就是说，我们将教这个奇异的 NanoNeuron 将温度从摄氏度转换（预测）为华氏度。

顺便说一句，摄氏温度转换为华氏温度的公式是这样的：

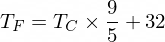
但目前我们的 NanoNeuron 还不知道......

纳米神经元模型

让我们实现 NanoNeuron 模型函数。它实现了x和y之间的基本线性依赖关系，类似于y = w * x + b 。简单地说，我们的 NanoNeuron 是“学校”中的一个“孩子”，正在被教导如何在XY坐标中画直线。

变量w 、 b是模型的参数。 NanoNeuron 只知道线性函数的这两个参数。这些参数是 NanoNeuron 在训练过程中要“学习”的东西。

NanoNeuron 唯一能做的就是模仿线性依赖。在它的predict()方法中，它接受一些输入x并预测输出y 。这里没有魔法。

 function NanoNeuron ( w , b ) {
  this . w = w ;
  this . b = b ;
  this . predict = ( x ) => {
    return x * this . w + this . b ;
  }
}

（...等等...线性回归是你吗？） ？

摄氏度 到 华氏度 转换

可以使用以下公式将摄氏温度值转换为华氏温度： f = 1.8 * c + 32 ，其中c是摄氏温度， f是计算出的华氏温度。

 function celsiusToFahrenheit ( c ) {
  const w = 1.8 ;
  const b = 32 ;
  const f = c * w + b ;
  return f ;
} ;

最终，我们希望教我们的 NanoNeuron 模仿这个函数（学习w = 1.8和b = 32 ），而无需提前知道这些参数。

这是摄氏度到华氏度转换函数的样子：

生成数据集

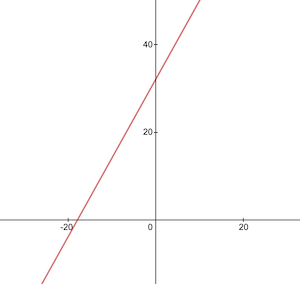
在训练之前，我们需要根据celsiusToFahrenheit()函数生成训练和测试数据集。数据集由成对的输入值和正确标记的输出值组成。

在现实生活中，在大多数情况下，这些数据是被收集而不是生成的。例如，我们可能有一组手绘数字图像以及相应的一组数字，用于解释每张图片上写的数字。

我们将使用 TRAINING 示例数据来训练我们的 NanoNeuron。在我们的 NanoNeuron 成长并能够自行做出决策之前，我们需要使用训练示例来教它什么是对的，什么是错的。

我们将使用测试示例来评估我们的 NanoNeuron 在训练期间未看到的数据上的表现如何。这时我们可以看到我们的“孩子”已经长大并且可以自己做决定了。

 function generateDataSets ( ) {
  // xTrain -> [0, 1, 2, ...],
  // yTrain -> [32, 33.8, 35.6, ...]
  const xTrain = [ ] ;
  const yTrain = [ ] ;
  for ( let x = 0 ; x < 100 ; x += 1 ) {
    const y = celsiusToFahrenheit ( x ) ;
    xTrain . push ( x ) ;
    yTrain . push ( y ) ;
  }

  // xTest -> [0.5, 1.5, 2.5, ...]
  // yTest -> [32.9, 34.7, 36.5, ...]
  const xTest = [ ] ;
  const yTest = [ ] ;
  // By starting from 0.5 and using the same step of 1 as we have used for training set
  // we make sure that test set has different data comparing to training set.
  for ( let x = 0.5 ; x < 100 ; x += 1 ) {
    const y = celsiusToFahrenheit ( x ) ;
    xTest . push ( x ) ;
    yTest . push ( y ) ;
  }

  return [ xTrain , yTrain , xTest , yTest ] ;
}

预测的成本（误差）

我们需要一些指标来显示模型的预测与正确值的接近程度。将使用以下公式计算y的正确输出值与我们的 NanoNeuron 创建的prediction之间的成本（错误）：

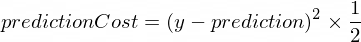
这是两个值之间的简单差异。值彼此越接近，差异越小。我们在这里使用2的幂只是为了消除负数，以便(1 - 2) ^ 2与(2 - 1) ^ 2相同。除以2只是为了进一步简化反向传播公式（见下文）。

在这种情况下，成本函数将非常简单：

 function predictionCost ( y , prediction ) {
  return ( y - prediction ) ** 2 / 2 ; // i.e. -> 235.6
}

前向传播

进行前向传播意味着对xTrain和yTrain数据集中的所有训练示例进行预测，并计算这些预测的平均成本。

此时，我们只是让 NanoNeuron 说出它的意见，只允许它猜测如何转换温度。这里可能是愚蠢的错误。平均成本将告诉我们我们的模型现在有多么错误。这个成本值非常重要，因为更改 NanoNeuron 参数w和b并再次进行前向传播；我们将能够评估这些参数改变后我们的 NanoNeuron 是否变得更聪明。

平均成本将使用以下公式计算：

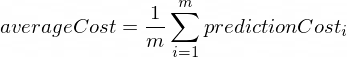
其中m是训练示例的数量（在我们的例子中： 100 ）。

下面是我们如何在代码中实现它：

 function forwardPropagation ( model , xTrain , yTrain ) {
  const m = xTrain . length ;
  const predictions = [ ] ;
  let cost = 0 ;
  for ( let i = 0 ; i < m ; i += 1 ) {
    const prediction = nanoNeuron . predict ( xTrain [ i ] ) ;
    cost += predictionCost ( yTrain [ i ] , prediction ) ;
    predictions . push ( prediction ) ;
  }
  // We are interested in average cost.
  cost /= m ;
  return [ predictions , cost ] ;
}

向后传播

当我们知道 NanoNeuron 的预测有多正确或错误时（基于此时的平均成本），我们应该做什么来使预测更加精确？

反向传播给了我们这个问题的答案。反向传播是评估预测成本并调整 NanoNeuron 参数w和b的过程，以便下一个和未来的预测更加精确。

这就是机器学习看起来神奇的地方？‍♂️。这里的关键概念是导数，它显示了要采取什么步骤来接近成本函数最小值。

请记住，找到成本函数的最小值是训练过程的最终目标。如果我们发现w和b值使得我们的平均成本函数很小，则意味着 NanoNeuron 模型确实可以做出很好且精确的预测。

衍生品是一个大而独立的主题，我们不会在本文中讨论。 MathIsFun 是一个很好的资源，可以帮助您基本了解它。

关于导数的一件事将帮助您理解反向传播的工作原理，那就是导数，就其含义而言，是函数曲线的一条切线，指向函数最小值的方向。

图片来源：MathIsFun

例如，在上图中，您可以看到，如果我们位于(x=2, y=4)点，那么斜率会告诉我们left和down移动以达到函数最小值。另请注意，斜率越大，我们移动到最小值的速度就越快。

参数w和b的averageCost函数的导数如下所示：

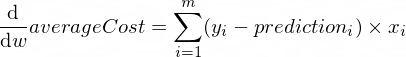
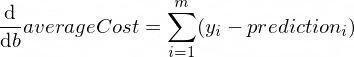
其中m是训练示例的数量（在我们的例子中： 100 ）。

您可以在此处阅读有关导数规则以及如何获得复杂函数的导数的更多信息。

 function backwardPropagation ( predictions , xTrain , yTrain ) {
  const m = xTrain . length ;
  // At the beginning we don't know in which way our parameters 'w' and 'b' need to be changed.
  // Therefore we're setting up the changing steps for each parameters to 0.
  let dW = 0 ;
  let dB = 0 ;
  for ( let i = 0 ; i < m ; i += 1 ) {
    dW += ( yTrain [ i ] - predictions [ i ] ) * xTrain [ i ] ;
    dB += yTrain [ i ] - predictions [ i ] ;
  }
  // We're interested in average deltas for each params.
  dW /= m ;
  dB /= m ;
  return [ dW , dB ] ;
}

训练模型

现在我们知道如何评估所有训练集示例的模型的正确性（前向传播）。我们还知道如何对 NanoNeuron 模型的参数w和b进行小调整（反向传播）。但问题是，如果我们只运行一次前向传播，然后再运行一次反向传播，我们的模型不足以从训练数据中学习任何规律/趋势。您可以将其与孩子上一天小学进行比较。他/她不应该去学校一次，而是日复一日、年复一年地去学习一些东西。

所以我们需要多次重复我们的模型的前向和后向传播。这正是trainModel()函数的作用。它就像我们 NanoNeuron 模型的“老师”：

• 它将花费一些时间（ epochs ）来处理我们有点愚蠢的 NanoNeuron 模型，并尝试训练/教授它，
• 它将使用特定的“书籍”（ xTrain和yTrain数据集）进行训练，
• 它将通过使用学习率参数alpha促使我们的孩子更加努力（更快）地学习

关于学习率alpha几句话。这只是我们在反向传播过程中计算出的dW和dB值的乘数。因此，导数为我们指明了寻找成本函数最小值（ dW和dB符号）所需的方向，并且还向我们展示了朝该方向需要多快的速度（ dW和dB的绝对值）。现在我们需要将这些步长乘以alpha以将我们的移动速度调整到最小值，更快或更慢。有时，如果我们对alpha使用较大的值，我们可能会简单地跳过最小值而永远找不到它。

与老师的类比是，他/她越用力地逼我们的“纳米孩子”，我们的“纳米孩子”学得就越快，但如果老师逼得太紧，“孩子”就会精神崩溃并获胜。学不到任何东西？

以下是我们如何更新模型的w和b参数：

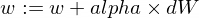
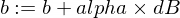
这是我们的训练器函数：

 function trainModel ( { model , epochs , alpha , xTrain , yTrain } ) {
  // The is the history array of how NanoNeuron learns.
  const costHistory = [ ] ;

  // Let's start counting epochs.
  for ( let epoch = 0 ; epoch < epochs ; epoch += 1 ) {
    // Forward propagation.
    const [ predictions , cost ] = forwardPropagation ( model , xTrain , yTrain ) ;
    costHistory . push ( cost ) ;
  
    // Backward propagation.
    const [ dW , dB ] = backwardPropagation ( predictions , xTrain , yTrain ) ;
  
    // Adjust our NanoNeuron parameters to increase accuracy of our model predictions.
    nanoNeuron . w += alpha * dW ;
    nanoNeuron . b += alpha * dB ;
  }

  return costHistory ;
}

把所有的部分放在一起

现在让我们使用上面创建的函数。

让我们创建 NanoNeuron 模型实例。此时 NanoNeuron 不知道应该为参数w和b设置什么值。所以让我们随机设置w和b 。

 const w = Math . random ( ) ; // i.e. -> 0.9492
const b = Math . random ( ) ; // i.e. -> 0.4570
const nanoNeuron = new NanoNeuron ( w , b ) ;

生成训练和测试数据集。

 const [ xTrain , yTrain , xTest , yTest ] = generateDataSets ( ) ;

让我们以小增量 ( 0.0005 ) 步长训练模型70000个周期。您可以使用这些参数，它们是根据经验定义的。

 const epochs = 70000 ;
const alpha = 0.0005 ;
const trainingCostHistory = trainModel ( { model : nanoNeuron , epochs , alpha , xTrain , yTrain } ) ;

让我们检查一下成本函数在训练期间如何变化。我们预计培训后的成本会比之前低很多。这意味着 NanoNeuron 变得更聪明。相反的情况也是可能的。

 console . log ( 'Cost before the training:' , trainingCostHistory [ 0 ] ) ; // i.e. -> 4694.3335043
console . log ( 'Cost after the training:' , trainingCostHistory [ epochs - 1 ] ) ; // i.e. -> 0.0000024

这就是训练成本随时代的变化的情况。 x轴上是纪元号 x1000。

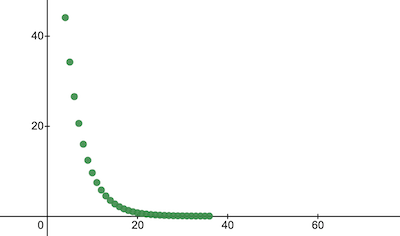
让我们看一下 NanoNeuron 参数，看看它学到了什么。我们期望 NanoNeuron 参数w和b与celsiusToFahrenheit()函数中的参数相似（ w = 1.8和b = 32 ），因为我们的 NanoNeuron 试图模仿它。

 console . log ( 'NanoNeuron parameters:' , { w : nanoNeuron . w , b : nanoNeuron . b } ) ; // i.e. -> {w: 1.8, b: 31.99}

评估测试数据集的模型准确性，看看我们的 NanoNeuron 处理新的未知数据预测的效果如何。测试集预测的成本预计将接近训练成本。这意味着我们的 NanoNeuron 在已知和未知数据上表现良好。

 [ testPredictions , testCost ] = forwardPropagation ( nanoNeuron , xTest , yTest ) ;
console . log ( 'Cost on new testing data:' , testCost ) ; // i.e. -> 0.0000023

现在，由于我们看到我们的 NanoNeuron“孩子”在训练期间在“学校”表现良好，并且他可以正确地将摄氏温度转换为华氏温度，即使对于它没有见过的数据，我们可以称其为“聪明”并问他一些问题。这是整个训练过程的最终目标。

 const tempInCelsius = 70 ;
const customPrediction = nanoNeuron . predict ( tempInCelsius ) ;
console . log ( `NanoNeuron "thinks" that ${ tempInCelsius } °C in Fahrenheit is:` , customPrediction ) ; // -> 158.0002
console . log ( 'Correct answer is:' , celsiusToFahrenheit ( tempInCelsius ) ) ; // -> 158

这么近！与我们所有人一样，我们的 NanoNeuron 很好，但并不理想:)

祝你学习愉快！

如何启动 NanoNeuron

您可以克隆存储库并在本地运行它：

git clone https://github.com/trekhleb/nano-neuron.git
cd nano-neuron

node ./NanoNeuron.js

跳过机器学习概念

为了简化解释，跳过并简化了以下机器学习概念。

训练/测试数据集分割

通常你有一大组数据。根据该集中的示例数量，您可能希望按 70/30 的比例将其拆分为训练/测试集。集合中的数据应该在分割之前随机打乱。如果示例数量很大（即数百万），则训练/测试数据集的分割比例可能接近 90/10 或 95/5。

网络带来力量

通常您不会注意到仅使用一个独立神经元。力量就在于这些神经元的网络。网络可能会学习更复杂的特征。 NanoNeuron 本身看起来更像是一个简单的线性回归，而不是神经网络。

输入标准化

在训练之前，最好对输入值进行标准化。

矢量化实现

对于网络，矢量化（矩阵）计算比for循环快得多。通常，如果以向量化形式实现并使用 Numpy Python 库等进行计算，则前向/后向传播的工作速度会更快。

成本函数的最小值

我们在本例中使用的成本函数过于简化。它应该具有对数分量。更改成本函数也会更改其导数，因此反向传播步骤也将使用不同的公式。

激活函数

通常，神经元的输出应该通过 Sigmoid 或 ReLU 等激活函数传递。

作者

• @trekhleb