Noise Reduction
1.0.0
关于项目
技术堆栈
文件结构
入门
结果和演示
未来的工作
贡献者
致谢和资源
执照
需要删除噪声，这是自然诱导的，就像非环境噪声一样，该噪声通过信号的降解而被去除。还请参考此文档有关AI降噪的博客
使用用于音频操纵的天秤座库。
对于我们使用Scipy的音频信号
Matplotlib用于操纵数据并可视化信号。
其余的对于数学操作而言是庞大的，在波浪文件上操作的浪潮。
Noise Reduction ├───docs ## Documents and Images │ └───Input Audio file ├─── Project Details │ | │ ├─── │ │ ├───Research papers │ │ ├───Linear Algebra │ │ ├───Neural networks & Deep Learning │ │ ├───Project Documentation │ │ ├───AI Noise Reduction Blog │ │ ├───AI Noise Reduction Report │ │ └───Code Implementation │ │ ├───AI Noise Reduction.py │ │ ├───audio.wav │ │ ├───Resources
在窗户上测试
git克隆https://github.com/dhriti03/noise-reduction.gitcd噪音 - 还原
在您的笔记本中安装某些库
PIP安装波 PIP安装libreosa PIP安装scipy.io PIP安装matplotlib.pyplot
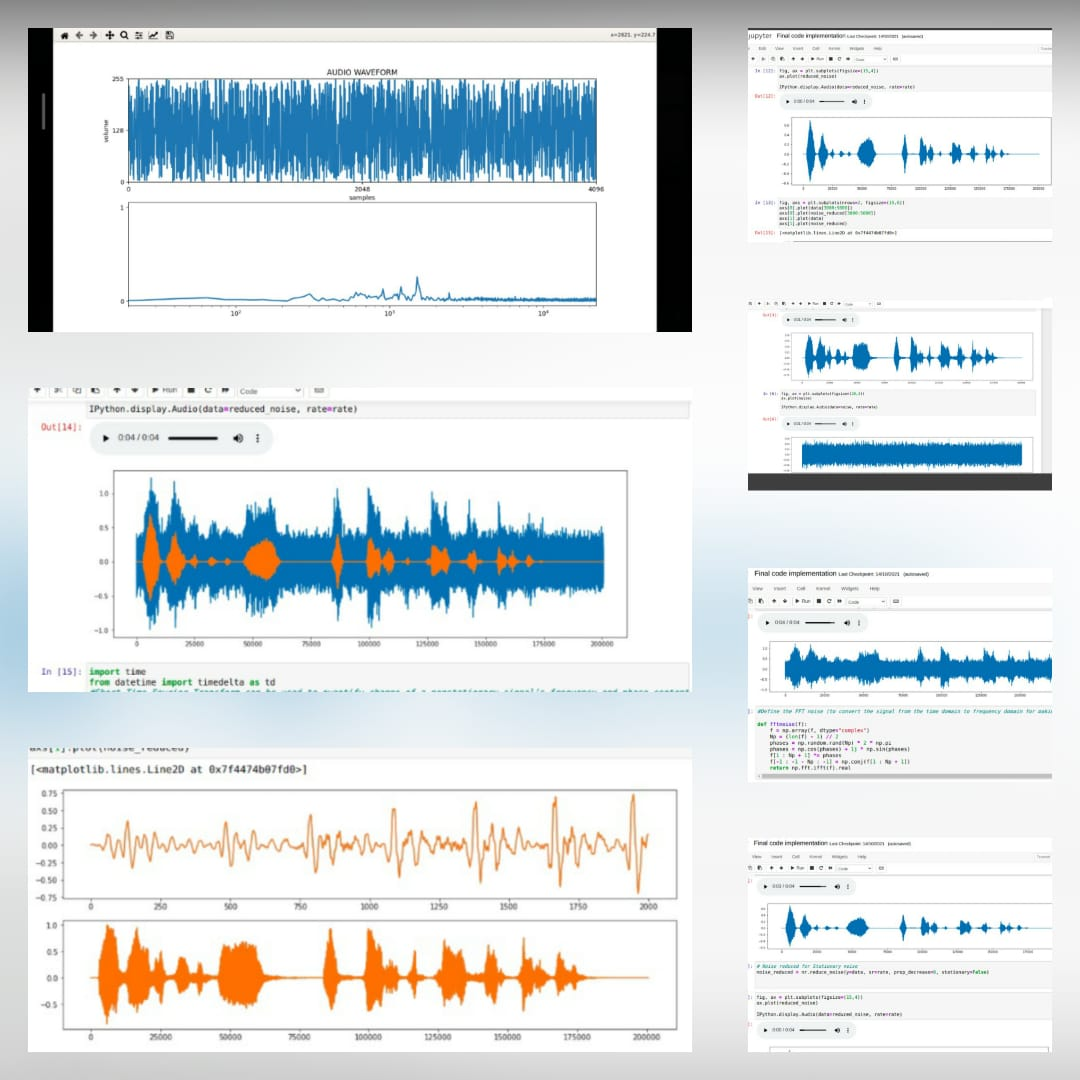
*这是原始音频文件 *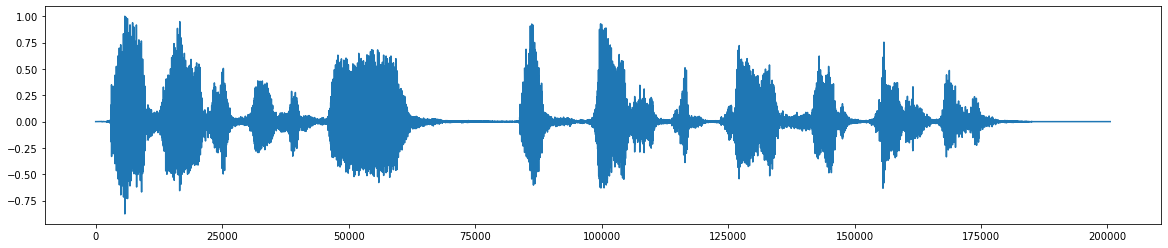 
*添加噪音 *之后 * 
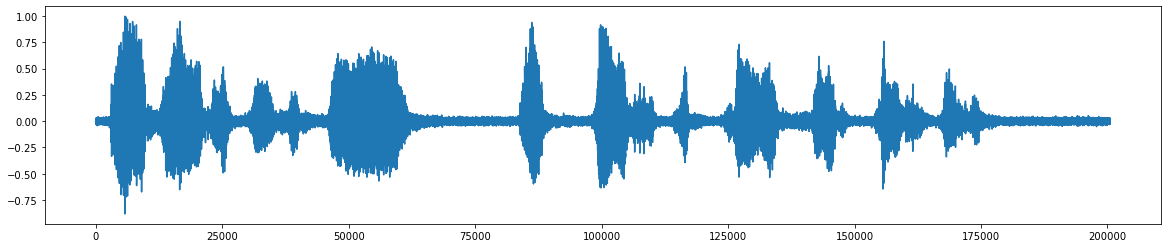*删除噪声后的最终音频信号 * 
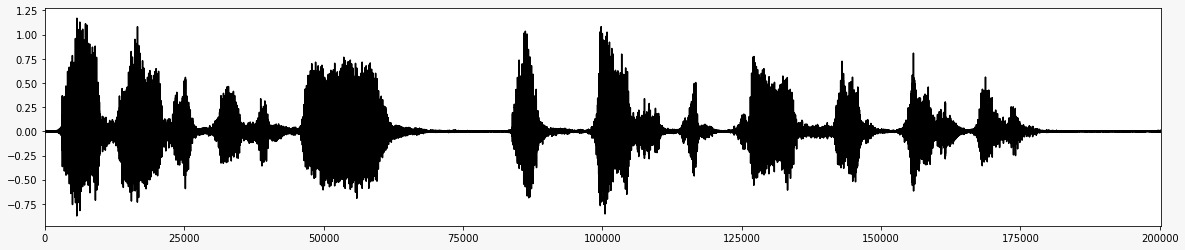*该项目的流程图 *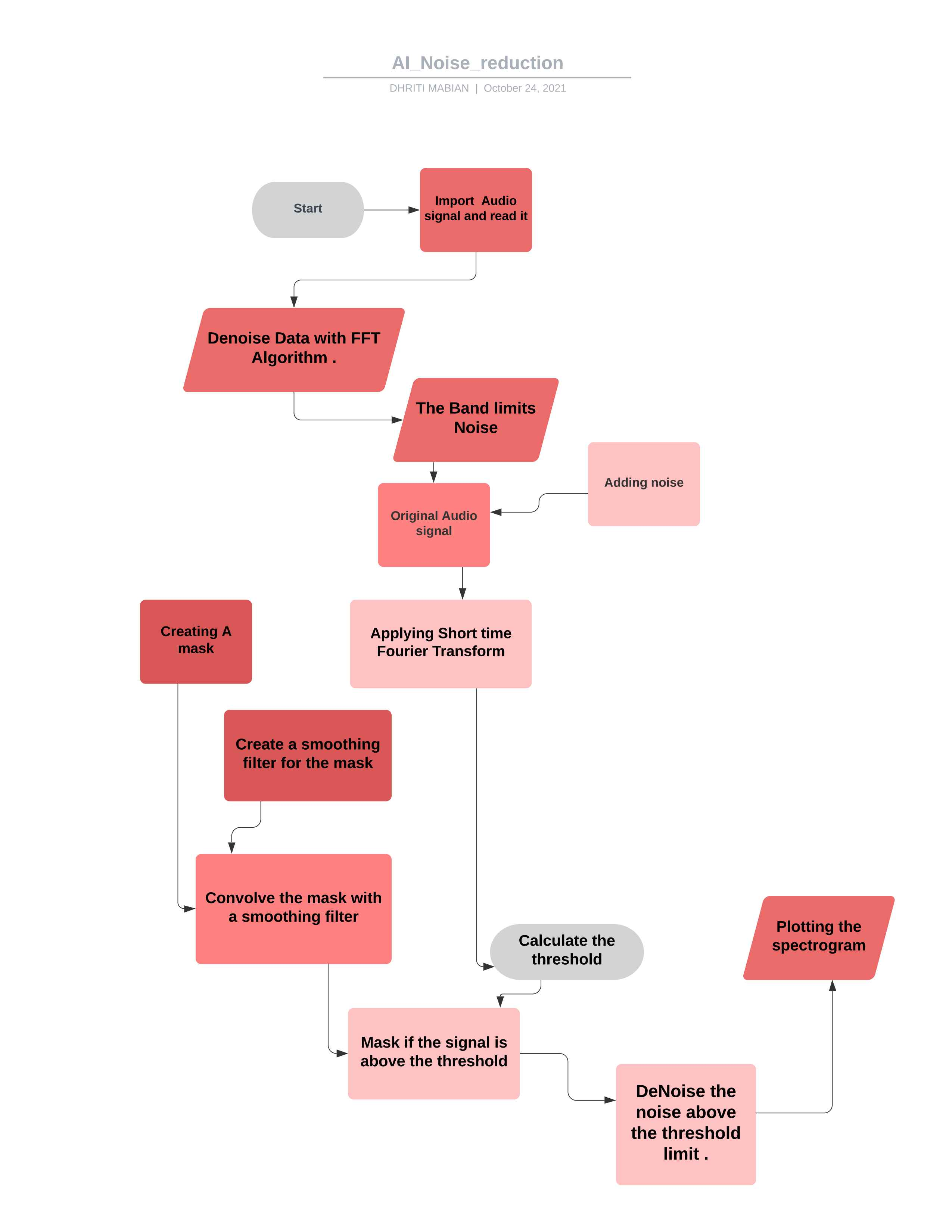 
根据您的要求操纵代码，您可以使用它来控制大多数音频符号。 ＃＃理论
在噪声音频剪辑上计算FFT
统计数据是根据噪声的FFT计算的（频率）
根据噪声的统计数据（以及算法的所需灵敏度）计算阈值
通过将信号FFT与阈值进行比较来确定掩码
在频率和时间上使用过滤器使掩模平滑
面具被添加到信号的FFT上，并倒置
从scipy.io导入ipython import wavfileimport scipy.signalimport numpy as npimport matplotlib.pyplot作为pltimport libresaimport wave％matplotlib inline
在这里，我们正在进口图书馆，例如用于创建用于交互式和探索性计算的全面环境的iPython lib。
从scipy.io库中，使用多种python命令来操纵数据和可视化数据。
Numpy包含多维阵列和矩阵数据结构。因此，它可以用于对诸如三角，统计和代数例程等数组进行许多数学操作，因此是一个非常有用的库。
matplotlib.pyplot库有助于通过不同的可视化来理解大量数据。
Libersa使用音乐生成（使用LSTM），自动语音识别（使用LSTM）等音频数据时使用。它提供了创建音乐信息检索系统所需的构建块。
％matplotlib inline启用了内联绘图，该图将在绘图命令写在的单元格下方。它提供了与jupyter笔记本等前端中后端的互动性。
wav_loc = r'/home/noings_reduction/downloads/wave/file.wav'rate，data = wavfile.read（wav_loc，mmap = false）
在这里，我们采用WAW文件路径位置，然后使用来自Scipy.io库的WaveFile模块读取WAW文件。使用参数（文件名 - 字符串或打开文件句柄，是输入WAV文件。）然后（mmap：bool，可选的，其中是否将数据读取为内存映射（默认值：false）。
def fftnoise（f）：f = np.Array（f，dtype =“复杂”）np =（len（f） - 1）// 2lase = np.random.rand.rand（np） * 2 * np.piphases = np 。 ）返回np.fft.ifft（f）
在这里，我们首先简要定义FFT噪声函数，快速傅立叶变换（FFT）是一种计算序列或其逆（IDFT）的离散傅立叶变换（DFT）的算法。傅立叶分析将信号从其原始域（通常是时间或空间）转换为频域中的表示形式，反之亦然。 DFT是通过将一系列值分解为不同频率的组件来获得的。
使用快速傅立叶变换并定义数据类型复杂的函数，最后计算函数的实际部分。在此，将最小频率和最大频率之间的频率设置为1，而休息不需要的频率被忽略了。
提供文件位置
读取WAV文件
-32767至+32767是适当的音频（对称），而32768表示在此时剪辑的音频
wav-file是16位整数，范围为[-32768，32767]，因此除以32768（2^15），将给出[-1，1]的适当的二组配件范围
def band_limited_noise（min_freq，max_freq，samples = 1024，采样= 1）：freqs = np.abs（np.fft.fft.fftfreq（samples，1 / samples，1 / sampleaser）f = np.法（样本> = min_freq，freqs <= max_freq）] = 1返回fftnoise（f）
函数或时间序列的傅立叶变换仅限于有限的频率或波长范围。
用标准FREQ定义最小限制和最大限制的FREQ。
noings_len = 2＃secondsnoise = band_limited_noise（min_freq = 4000，max_freq = 12000，samples = len（data），samplerate = rate = rate）*10noise_clip = noiese [：reside diesuct [速度*noye_len] audio_clip_band_band_limited = data+data+data+data+dogati
带限制的白噪声块指定了两侧光谱，其中单元为Hz。
将最大为12000和最小频率为4000的最小频率，将噪声和所提供的数据进行比较。
在这里，我们通过具有速率的产物和噪声信号的LEN来剪辑噪声信号。
因此添加了噪声和给定的数据
实际上，添加噪声扩大了训练数据集的大小。
随机噪声被添加到输入变量中，每次暴露于模型时它们都会不同。
在输入样本中添加噪声是一种简单的数据增强形式。
添加噪声意味着网络无法记住培训样本，因为它们一直在改变，
导致较小的网络权重和一个更健壮的网络，其概括误差较低。
导入DateTime的时间导入TIMEDELTA为TD
导入时间该模块提供了各种与时间相关的功能。有关相关功能，另请参见DateTime和日历模块。类dateTime.timedelta
持续时间表达两个日期，时间或日期时间实例之间的差异到微秒分辨率。
def _stft（y，n_fft，hop_length，win_length）：返回blibrosa.stft（y = y，n_fft = n_fft = n_fft，hop_length = hop_length = hop_length，win_length = win_length）
短时间傅立叶变换可用于量化非组织信号的频率和相位内容随时间的变化。
跳长应指连续帧之间的样本数量。对于信号分析，HOP长度应小于帧大小，因此帧重叠。
参数ynp.ndarray [shape =（n，）]，实价输入信号
N_FFTINT> 0 [标量]
用零填充后的窗户信号的长度。 STFT矩阵D中的行数为（1 + N_FFT/2） 。默认值N_FFT = 2048样品，对应于93毫秒的物理持续时间，采样速率为22050 Hz，即Librosa中的默认采样率。该值适用于音乐信号。但是，在语音处理中，推荐的值为512，对应于23毫秒，采样速率为22050 Hz。无论如何，我们建议将N_FFT设置为两个功率，以优化快速傅立叶变换（FFT）算法的速度。
hop_lengthint> 0 [标量]
相邻STFT列之间的音频样本数。
较小的值增加了D中的列数，而不会影响STFT的频率分辨率。
如果未指定，则默认为win_length // 4（见下文）。
win_lengthint <= n_fft [标量]
每个音频框架都用长度win_length的窗口窗口，然后用零填充以匹配N_FFT 。
较小的值改善了STFT的时间分辨率（即，以频率分辨率为代价（即区分频率紧密间隔的纯音调的能力）以牺牲频率分辨率为代价）。这种效果称为时频定位权衡取舍，需要根据输入信号y的属性进行调整。
如果未指定，则默认为win_length = n_fft 。
返回libresa.istft（y，hop_length，win_length）
反向短时傅立叶变换（ISTFT）。通过最大程度地降低stft_matrix和y之间的平方平方误差和y之间的平方误差，将复合物值频谱stft_matrix转化为y。
通常，窗口函数，跳长和其他参数应与STFT相同，这主要导致来自未修改的STFT_MATRIX的信号的完美重建。
def _amp_to_db（x）：返回libreosa.core.mplitude_to_db（x，ref = 1.0，amin = 1e-20，top_db = 80.0）
1.将振幅光谱图转换为DB尺度频谱图。这等同于power_to_db（s ** 2），但为方便起见提供。
返回libreosa.core.db_to_amplitude（x，ref = 1.0）
将DB尺度的光谱图转换为振幅光谱图。
这有效地反转振幅_to_db：
db_to_amplitude（s_db）〜= 10.0 （0.5*（s_db + log10（ref）/10））**
def plot_spectRogram（信号，标题）：图，ax = plt.subplots（figsize =（20，4））cax = ax.matshow（信号，origin，origin =“ lower”，factor =“ auto”，cmap = plt.cm。地震，vmin = -1 * np.max（np.abs（signal）），vmax = np.max（np.abs（signal）），
）用信号作为输入绘制镜头。
轴类包含大多数图元素：轴，tick，line2d，文本，多边形等，并设置坐标系。
它在Matplotlib中提供了可通过此功能访问的多个颜色地图。
图。Colorbar（CAX）AX.SET_TITLE（标题）
查看发生的事情的最佳方法是添加一个配色键（创建散点图之后）。您会注意到，0到10000之间的外观值全部低于条的最低部分，那里的东西非常浅绿色。
通常，Vmin以下的值将以最低的颜色颜色，而Vmax上方的值将获得最高的颜色。
如果您将VMAX小于VMIN设置，则在内部将交换它们。尽管根据Matplotlib的确切版本和所谓的精确函数，Matplotlib可能会发出错误警告。因此，最好将VMIN设置为始终低于Vmax。
def plot_statistics_and_filter（mean_freq_noise，std_freq_noise，noings_thresh，smoothing_filter）：图，ax = plt.subplots（ncols = 2，figsize = 2，figsize =（20，4））噪音”））
plt_std，= ax [0] .plot（noye_thresh，label =“噪声阈值（按频率）”）ax [0] .set_title（“蒙版的阈值”）
ax [0] .legend（）cax = ax [1] .matshow（smoothing_filter，origin =“ lower”）fic.colorbar（cax）ax [1] .set_title（“平滑蒙版的滤镜”）绘制了降噪的基本统计数据。
信噪比（SNR或S/N）是科学和工程中使用的措施，将所需信号的水平与背景噪声水平进行比较。
SNR定义为信号功率与噪声功率的比率，通常在分贝中表达。
高于1：1（大于0 dB）的比率比噪声更多的信号。
设置噪声掩蔽的阈值频率。
掩盖阈值是指由于另一种声音的存在，使一种声音听不见。
因此，掩盖阈值是在存在另一种称为“掩蔽器”的噪音的情况下使声音可听见的声音的声音水平
因此增加了阈值。
模糊的噪声信号具有各种低通滤波器
将定制过滤器应用于图像（2D卷积）
def emovenoise（＃要平均三角波的正斜率部分（上升）的信号（电压），以尝试删除尽可能多的噪声。audio_clip，＃这些剪辑是我们使用的参数，操作noiese_clip，n_grad_freq = 2，＃使用掩码平滑的频率频道。 2048，＃由``窗口''窗口的每个音频窗口'窗口窗口的长度为`win_length'，然后用零填充``n_fft`..hop_length = 512'' n_std_thresh = 1.5，＃比噪声的平均db（在每个频率级别）被视为signalProp_decrease = 1.0，＃在多大程度上降低噪声（1 = all，0 = none）derbose = false ，＃标志允许您编写外观呈现的正则表达式= false，＃是绘制算法的步骤）：
def emovenoise（平均为三角波的正斜率部分（上升）的信号（电压），以试图消除尽可能多的噪声。
audio_clip，
这些剪辑是我们要进行各自操作的参数
noings_clip， n_grad_freq = 2用掩模平滑多少个频道。
n_grad_time = 4，用掩码平滑多少个时间通道。
N_FFT = 2048
STFT列之间帧的数字音频。
win_length = 2048，每个音频帧均由window()窗口。该窗口的长度为win_length ，然后用零填充以匹配n_fft 。
hop_length = 512， sTFT列之间帧的数字音频。
N_STD_THRESH = 1.5比噪声的平均db（在每个频率级别上）要被视为信号的标准偏差大多数
prop_decrease = 1.0，您应在多大程度上降低噪声（1 =全部，0 =无）
冗长= false，
标志允许您编写看起来像visual = false的正则表达式， ＃是绘制算法的步骤）：
noings_stft = _stft（noings_clip，n_fft，hop_length，win_length）noiese_stft_db = _amp_to_db（np.abs（noings_stft））
STFT上的噪音
转换为DB
mean_freq_noise = np.mean（noings_stft_db，axis = 1）std_freq_noise = np.std（noings_stft_db，axis = 1）
计算噪声的统计数据
在这里，我们为阈值噪声添加了平均值和标准噪声和N_STD噪声。
sig_stft = _stft（audio_clip，n_fft，hop_length，win_length）sig_stft_db = _amp_to_db（np.abs（sig_stft））
STFT在信号上
mask_gain_db = np.min（_amp_to_db（np.abs（sig_stft））））
将值计算为掩码数据库
Smootying_filter = np.outer（np.concatenate（concatenate）（
[np.linspace（0，1，n_grad_freq + 1，endpoint = false），np.linspace（1，0，n_grad_freq + 2），
这是给出的
）[1：-1]，np.concatenate（
[np.linspace（0，1，n_grad_time + 1，endpoint = false），np.linspace（1，0，n_grad_time + 2），
这是给出的
）[1：-1]，
）Smoothing_filter = Smoothing_filter / np.sum（Smoothing_filter）在时间和频率上为掩模创建平滑过滤器
db_thresh = np.Repeat（np.Reshape（noings_thresh，[1，len（mean_freq_noise））），np.shape（sig_stft_db）[1]，axis = 0，，
）.t计算每个频率/时间箱的阈值
sig_mask = sig_stft_db <db_thresh
信号的蒙版
sig_mask = scipy.signal.fftconvolve（sig_mask，Smoothing_filter，mode =“ same”）sig_mask = sig_mask * prop_decrease
带平滑过滤器的掩盖卷积
＃掩盖信号_stft_db_masked =（sig_stft_db *（1 -sig_mask）+ np.ones（np.shape（mask_gain_db）） * mask_gain_gain_db * sig_mask）＃ _TO_AMP （sig_stft_db_masked） * np.sign（sig_stft）） +（1J * sig_imag_masked）
掩盖信号
＃恢复signalRecovered_signal = _istft（sig_stft_amp，hop_length，win_length）rectioned_spec = _amp_to_db（np.abs（_stft（_STFT（recuceed_signal，n_fft，n_fft，n_fft，hop_length，hop_length，win_length））
）恢复信号
因此，如果信号高于阈值，则施加掩码
用平滑过滤器卷动面具
为已经下载的WAV文件应用降噪算法。
在音频信号的实时记录上应用FFT。
进一步更深入地实施了AI的消除噪声。
将降噪算法应用于各种形式的音频文件。
带有麦克风和ESP32的实时音频信号，因此将获取WAV文件以进行进一步的计算和信号处理。
Dhriti Mabian
Priyal Awankar
*SRA vjti_eklavya 2021
Shreyas Atre
苛刻的沙阿
大胆
降噪方法
从马丁·亨氏（Martin Heinz）拿起样板
蒂姆·塞恩堡
执照
