Lanczos

蘭佐斯重採樣

介紹

Lanczos（發音為 Lanchos）重採樣是一種複雜的數位訊號插值技術，與最近鄰插值和雙線性插值等簡單方法相比，可提供卓越的影像品質。透過有效保留細節並最大限度地減少混疊偽影，Lanczos 重採樣廣泛應用於影像和訊號處理應用。

雖然 Lanczos 在影像品質方面表現出色，但它的代價是計算複雜性增加。此外，潛在的「振鈴」偽影（尤其是在銳利邊緣周圍）可能是一個缺點。儘管面臨這些挑戰，Lanczos 由於其整體性能優勢，仍然是圖像縮放和旋轉等任務的首選。

本文檔全面概述了 Lanczos 重採樣，包括其理論基礎、實現細節和實際應用。對於尋求理解和利用這種強大技術的開發人員和研究人員來說，它是寶貴的資源。隨後的部分深入研究 Lanczos 重採樣的關鍵方面，例如 Lanczos 核、插值和重採樣過程、通量保留、上採樣、下採樣、樣本定位、輸出範圍、多維插值和可分離性。包含一個帶有原始程式碼的實際範例。

蘭佐斯內核

針對給定支援大小定義的 Lanczos 核心是 Lanczos 重採樣中使用的函數。內核定義為：

 L(x) = sinc(x)*sinc(x/a) : -a < x < a
     = 0.0               : otherwise

在哪裡：

• x 是透過 Lanczos 視窗計算的自變數
• a是kernel的支撐尺寸，控制寬度

歸一化 sinc 函數定義為：

 sinc(x) = 1.0              : x = 0.0
        = sin(PI*x)/(PI*x) : otherwise

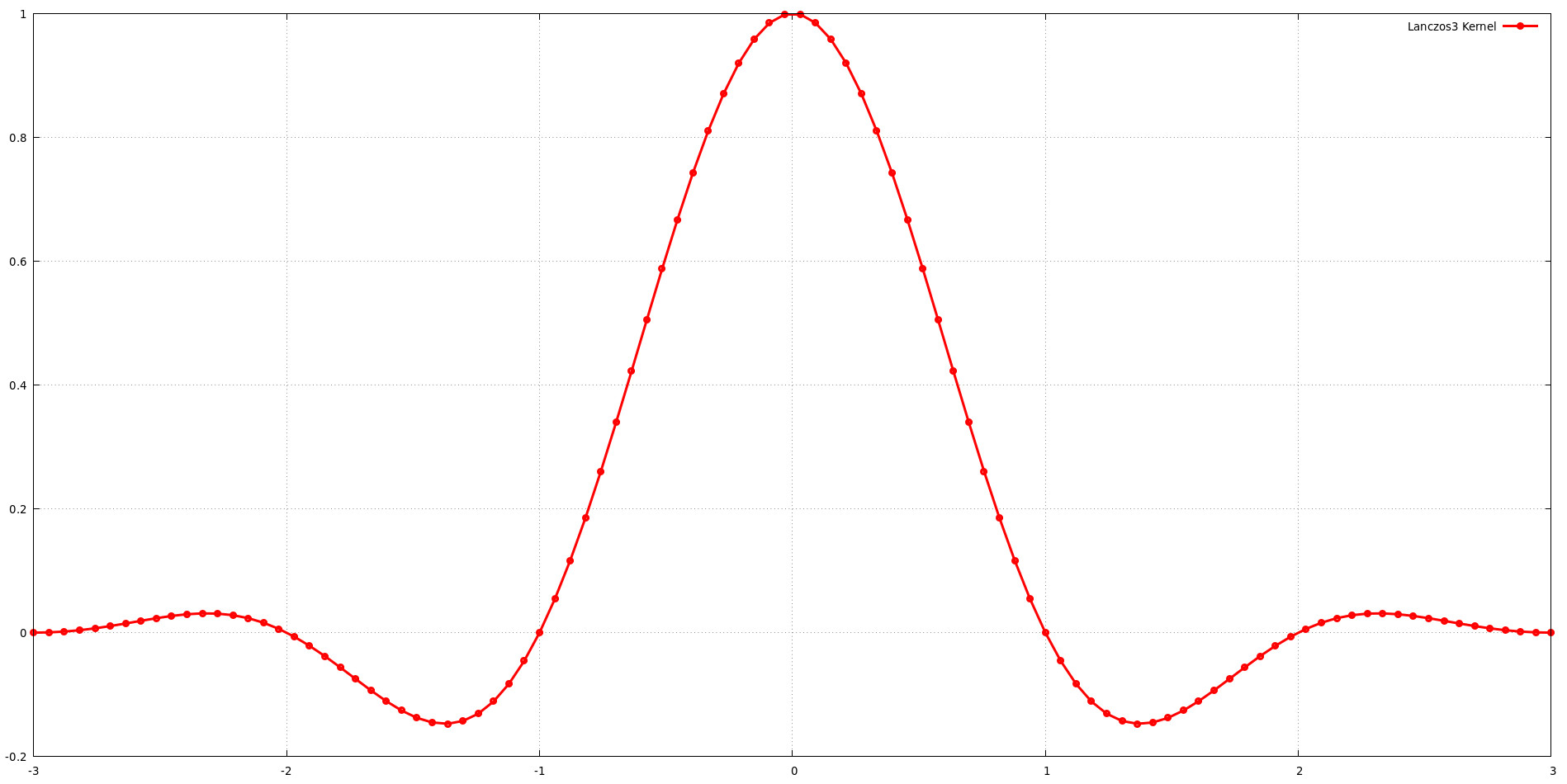
該圖說明了支援大小 a = 3 時 Lanczos 核的形狀。雖然增加支撐尺寸 (a) 通常可以為塑造頻率響應提供更大的靈活性，但它也會增加計算成本。選擇支撐尺寸時，必須在影像品質和運算效率之間取得平衡。 Jim Blinn 發現 a = 3 的 Lanczos 內核在低頻保留和高頻抑制之間實現了出色的平衡，這支持了這一觀點。

注意：術語「內核寬度」、「支援尺寸」和「濾波器尺寸」通常可互換使用來描述參數 a。然而，在 Lanczos 重採樣的背景下，「支援大小」最準確地反映了這個概念。

Lanczos 插值和重採樣

Lanczos 插值是一種用於將離散訊號重新取樣到新取樣率的技術。它透過將原始訊號與 Lanczos 內核進行卷積來實現這一點。

插值訊號 s2(x) 可以計算如下：

 s2(x) = (1/w(x))*
        SUM(i = -a + 1, i = a,
            s1(floor(x) + i)*
            L(i - x + floor(x)))

在哪裡：

• s1(x) 是原始輸入訊號，視為連續函數
• w(x) 是維持通量的歸一化因子

保持通量：

歸一化因子 w(x) 對於在插值過程中保留整體訊號能量或品質至關重要。它確保插值的總和接近原始樣本的總和。濾波器重量計算如下：

 w(x) = SUM(i = -a + 1, i = a, L(i - x + floor(x)))

上採樣：

當提高取樣率時，可以直接使用Lanczos插值方程，無需修改。

下採樣：

為了避免降低取樣率時出現混疊偽影，必須調整濾波器比例以符合新的取樣率。

 fs = n1/n2

s2(x) = (1/w(x))*
        SUM(i = -(fs*a) + 1, i = (fs*a),
            s1(floor(x) + i)*
            L((i - x + floor(x))/fs))

在哪裡：

• fs 是下取樣因子
• n1 是原始訊號中的樣本數
• n2 是插值訊號中的樣本數

職位範例

將訊號從 n1 個樣本重採樣到 n2 個樣本時，將使用以下樣本位置。索引j用於表示來自取樣訊號s2(x)的樣本。 (j + 0.5) 項是 s2(x) 中樣本的中心。此步驟將 s2(x) 中的點縮放到 s1(x) 中的點。 x 中的最後一項 -0.5 是導致 Lanczos 係數樣本偏移的相移。

 step = n1/n2
j    = [0..n2)
x    = (j + 0.5)*step - 0.5

邊緣處理

執行 Lanczos 插值時，必須特別注意訊號邊界。常見的邊緣處理技術包括：

• 零填充：用零將訊號擴展到原始範圍之外。
• 箝位：將邊緣值分配給訊號邊界之外的樣本。
• 鏡像：在邊界處反射訊號。
• 重複：多次重複邊緣值。

零填充：

 s1(x) = s1[floor(x)] : x = [0, n1)
      = 0.0          : otherwise

夾緊：

 s1(x) = s1[clamp(floor(x), 0, n1 - 1)]

箝位通常是首選，因為它可以減少由邊緣附近的尖銳不連續性引起的邊緣偽影。然而，邊緣處理方法的選擇取決於具體應用和所需的輸出。

輸出範圍

由於 L(x) 的波瓣，s2(x) 的範圍可能大於 s1(x) 的範圍。例如，[0.0,1.0]範圍內的像素顏色對應的輸入訊號s1(x)需要箝位到同一範圍，以確保轉換回[0,255]的無符號位元組時輸出值不會溢位。

多維插值

Lanczos 核可以擴展到多個維度，以對影像或更高維的資料執行插值。

二維 Lanczos 核定義為：

 L(x, y) = sinc(sqrt(x^2 + y^2))*sinc(sqrt(x^2 + y^2)/a)

插值訊號 s2(x, y) 可以使用以下公式計算：

 s2(x, y) = (1/w(x, y))*
           SUM(i = -a + 1, i = a,
               SUM(j = -a + 1, j = a,
                   s1(floor(x) + j, floor(y) + i)*
                   L(j - x + floor(x), i - y + floor(y))))

其中 w(x, y) 是使用二維 Lanczos 核計算的歸一化因子。

可分離性

與某些插值方法不同，Lanczos 核是不可分離的，這意味著它不能分解為一維核的乘積。與可分離內核相比，此屬性通常會導致更高的計算成本。為了提高效能，一些實作透過對水平和垂直維度執行單獨的傳遞來近似 Lanczos 核心。

水平插值：

• 將一維 Lanczos 核應用於輸入訊號 s1(x, y) 的每一行。
• 這會產生一個中間結果 s2(x, y)。

垂直插值：

• 將一維 Lanczos 核應用於中間結果 s2(x, y) 的每一列。
• 這會產生最終的插值訊號 s3(x, y)。

數學表示：

 s2(x, y) = (1/w(x))*
           SUM(j = -a + 1, j = a,
               s1(floor(x) + j, y)*
               L(j - x + floor(x)))

s3(x, y) = (1/w(y))*
           SUM(i = -a + 1, i = a,
               s2(x, floor(y) + i)*
               L(i - y + floor(y)))

請注意，歸一化因子 w(x) 和 w(y) 是使用一維 Lanczos 核計算的。

要點：

• 與全二維 Lanczos 插值相比，可分離近似顯著降低了計算成本。
• 然而，由於 Lanczos 內核不可分離組件的資訊遺失，它引入了偽影。
• 完全 Lanczos 插值和可分離近似之間的選擇取決於特定應用對質量和計算效率的要求。

類似地，對訊號進行多次遞歸重採樣（通常用於產生紋理 mipmap）也會因為每個重採樣步驟的誤差累積而降低影像品質。

例子

執行 lancos-test 範例並使用 gnuplot 查看 Lanczos 重採樣在按 2 倍上取樣和下取樣時如何影響簡單的一維訊號。

 make
./lanczos-test
gnuplot
> load "output.plot"

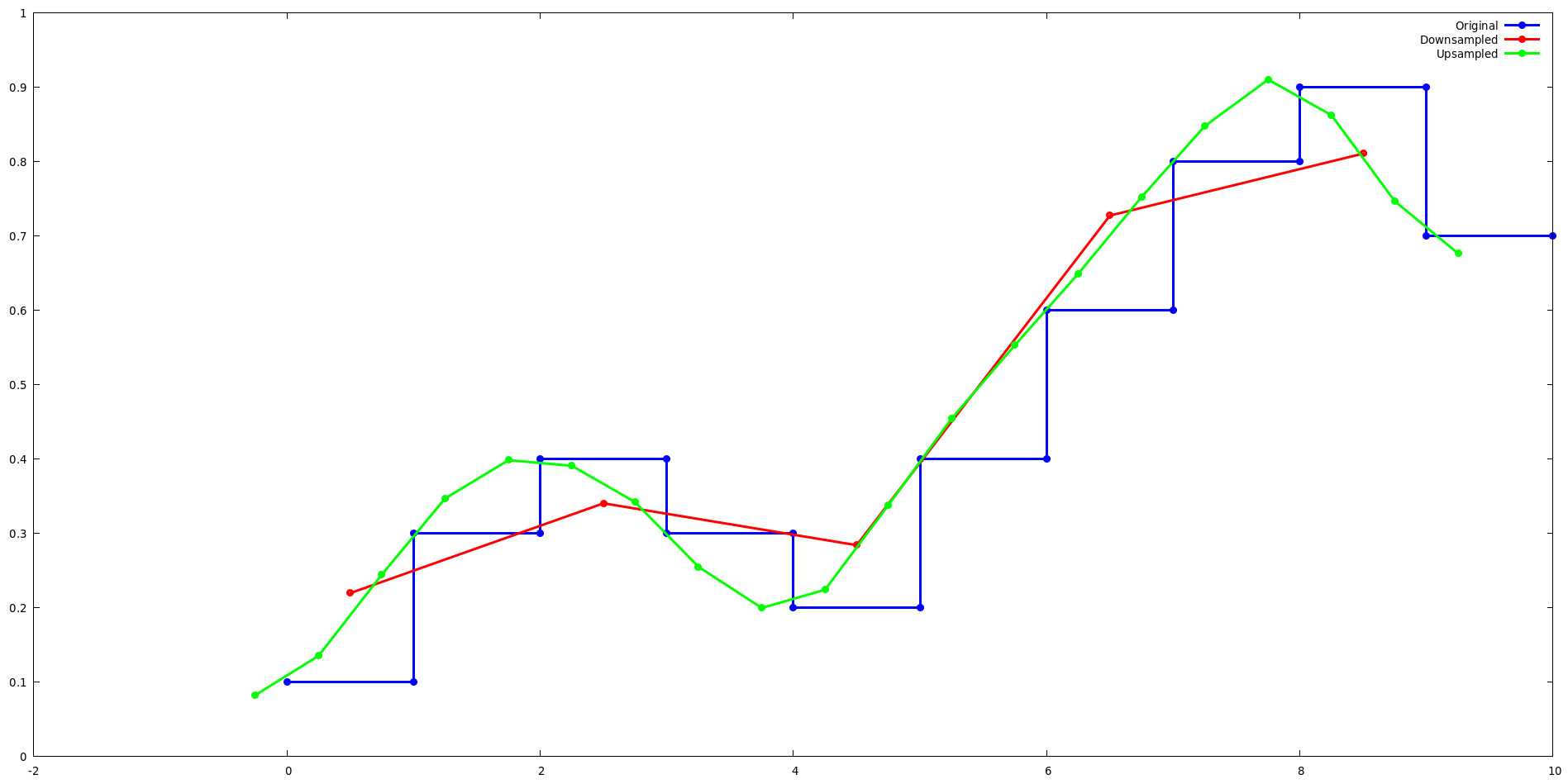
上採樣：

按 2 的冪進行上取樣時，Lanczos 內核在 2^level 組值之間會循環。例如，考慮 lanzcos-test 上取樣範例的前 4 個輸出。注意，L(x) 的輸出對於 j={0,2} 和 j={1,3} 重複。

 upsample n1=10, n2=20
j=0, x=-0.250000
i=-2, L(-2.750000)=0.007356, S1(-3.000000)=0.100000
i=-1, L(-1.750000)=-0.067791, S1(-2.000000)=0.100000
i=0, L(-0.750000)=0.270190, S1(-1.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(0.000000)=0.100000
i=2, L(1.250000)=-0.132871, S1(1.000000)=0.300000
i=3, L(2.250000)=0.030021, S1(2.000000)=0.400000
s2=0.082129, s2/w=0.082379, w=0.996972
j=1, x=0.250000
i=-2, L(-2.250000)=0.030021, S1(-2.000000)=0.100000
i=-1, L(-1.250000)=-0.132871, S1(-1.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(0.000000)=0.100000
i=1, L(0.750000)=0.270190, S1(1.000000)=0.300000
i=2, L(1.750000)=-0.067791, S1(2.000000)=0.400000
i=3, L(2.750000)=0.007356, S1(3.000000)=0.300000
s2=0.134869, s2/w=0.135279, w=0.996972
j=2, x=0.750000
i=-2, L(-2.750000)=0.007356, S1(-2.000000)=0.100000
i=-1, L(-1.750000)=-0.067791, S1(-1.000000)=0.100000
i=0, L(-0.750000)=0.270190, S1(0.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(1.000000)=0.300000
i=2, L(1.250000)=-0.132871, S1(2.000000)=0.400000
i=3, L(2.250000)=0.030021, S1(3.000000)=0.300000
s2=0.243853, s2/w=0.244594, w=0.996972
j=3, x=1.250000
i=-2, L(-2.250000)=0.030021, S1(-1.000000)=0.100000
i=-1, L(-1.250000)=-0.132871, S1(0.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(1.000000)=0.300000
i=1, L(0.750000)=0.270190, S1(2.000000)=0.400000
i=2, L(1.750000)=-0.067791, S1(3.000000)=0.300000
i=3, L(2.750000)=0.007356, S1(4.000000)=0.200000
s2=0.345945, s2/w=0.346996, w=0.996972

下採樣：

當以 2 的冪進行下取樣時，Lanczos 核心變得獨立於 x，因為 (x - Floor(x)) 成為與相移匹配的常數。例如，考慮 lanzcos-test 下取樣範例的前 2 個輸出。請注意，L(x) 的輸出對於每個 j 都是重複的。

 downsample n1=10, n2=5
j=0, x=0.500000
i=-5, L(-2.750000)=0.007356, S1(-5.000000)=0.100000
i=-4, L(-2.250000)=0.030021, S1(-4.000000)=0.100000
i=-3, L(-1.750000)=-0.067791, S1(-3.000000)=0.100000
i=-2, L(-1.250000)=-0.132871, S1(-2.000000)=0.100000
i=-1, L(-0.750000)=0.270190, S1(-1.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(0.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(1.000000)=0.300000
i=2, L(0.750000)=0.270190, S1(2.000000)=0.400000
i=3, L(1.250000)=-0.132871, S1(3.000000)=0.300000
i=4, L(1.750000)=-0.067791, S1(4.000000)=0.200000
i=5, L(2.250000)=0.030021, S1(5.000000)=0.400000
i=6, L(2.750000)=0.007356, S1(6.000000)=0.600000
s2=0.437796, s2/w=0.219563, w=1.993943
j=1, x=2.500000
i=-5, L(-2.750000)=0.007356, S1(-3.000000)=0.100000
i=-4, L(-2.250000)=0.030021, S1(-2.000000)=0.100000
i=-3, L(-1.750000)=-0.067791, S1(-1.000000)=0.100000
i=-2, L(-1.250000)=-0.132871, S1(0.000000)=0.100000
i=-1, L(-0.750000)=0.270190, S1(1.000000)=0.300000
i=0, L(-0.250000)=0.890067, S1(2.000000)=0.400000
i=1, L(0.250000)=0.890067, S1(3.000000)=0.300000
i=2, L(0.750000)=0.270190, S1(4.000000)=0.200000
i=3, L(1.250000)=-0.132871, S1(5.000000)=0.400000
i=4, L(1.750000)=-0.067791, S1(6.000000)=0.600000
i=5, L(2.250000)=0.030021, S1(7.000000)=0.800000
i=6, L(2.750000)=0.007356, S1(8.000000)=0.900000
s2=0.678627, s2/w=0.340344, w=1.993943

作為進一步的最佳化，可以針對這些情況預先計算 Lanczos 內核，以消除昂貴的 sinc 函數計算。

參考

本自述文件是在 Google Gemini 的幫助下創建的。

其他參考資料包括：

• 蘭佐斯重採樣
• Lanczos 插值和重採樣
• 插值演算法
• 常見重採樣任務的過濾器
• 枕頭實施
• 影像重採樣器

執照

該代碼由 Jeff Boody 根據 MIT 許可證實現。

 Copyright (c) 2024 Jeff Boody

Permission is hereby granted, free of charge, to any person obtaining a
copy of this software and associated documentation files (the "Software"),
to deal in the Software without restriction, including without limitation
the rights to use, copy, modify, merge, publish, distribute, sublicense,
and/or sell copies of the Software, and to permit persons to whom the
Software is furnished to do so, subject to the following conditions:

The above copyright notice and this permission notice shall be included
in all copies or substantial portions of the Software.

THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
THE SOFTWARE.