GGS

地質勘探局

貪心高斯分割 (GGS) 是一個 Python 求解器，用於有效分割多元時間序列資料。有關實施細節，請參閱我們的論文：http://stanford.edu/~boyd/papers/ggs.html。

---

GGS 解算器採用 n×T 資料矩陣，並將 n 維向量上的 T 個時間戳記分成多個片段，在這些片段上，資料可以很好地解釋為來自多元高斯分佈的獨立樣本。它透過制定協方差正則化最大似然問題並使用貪心啟發式解決該問題來實現這一點，論文中描述了完整的細節。

下載和設定

1. 透過執行以下命令在終端機中下載原始程式碼：

 git clone [email protected]:davidhallac/GGS.git

2. 透過執行以下命令確認程式碼已正確下載：

 cd GGS
python helloworld.py

3. 要編寫您自己的使用 ggs 的 Python 函數，只需確保ggs.py與新檔案位於同一目錄中，然後將以下程式碼新增至腳本的開頭：

 from ggs import *

支援的功能

GGS套件有三個主要功能：

 bps, objectives = GGS(data, Kmax, lamb)

在數據中尋找給定正則化參數 lambda 的 K 個斷點

輸入

data - n×T 資料矩陣，具有 n 維向量的 T 個時間戳

Kmax - 要找的斷點數量

羔羊 - 正規化協方差的正規化參數

退貨

bps - 列表的列表，其中較大列表的元素i是 GGS 演算法中在K = i處找到的斷點集

目標 - 每個中間步驟的目標值清單（ K = 0 到 Kmax）

---

 meancovs = GGSMeanCov(data, breakpoints, lamb)

給定一組斷點，找出每個段落的平均值和正規化協方差。

輸入

data - n×T 資料矩陣，具有 n 維向量的 T 個時間戳

斷點 - 斷點位置列表

羔羊 - 正規化協方差的正規化參數

退貨

meancovs - 資料中每個區段的（平均值、協方差）元組列表

---

 cvResults = GGSCrossVal(data, Kmax=25, lambList = [0.1, 1, 10])

執行 10 倍交叉驗證，並傳回每個 (K, lambda) 對的訓練集和測試集似然度，最高可達 Kmax

輸入

data - n×T 資料矩陣，具有 n 維向量的 T 個時間戳

Kmax - 運行 GGS 的最大斷點數

lambdaList - 要測試的正規化參數列表

退貨

cvResults -羔羊列表中每個正則化參數的（羔羊，（[TrainLL]，[TestLL]））元組列表。此處，TrainLL 和 TestLL 是從 0 到 Kmax 的所有K的 10 倍交叉驗證中的平均每個樣本對數似然

---

其他可選參數（對於上述所有三個功能）：

features = [] - 選擇資料中的某個列子集進行操作

verbose = False - 運行演算法時列印中間步驟

用法範例

執行financeExample.py將產生以下圖，顯示目標（論文中的公式 4）與斷點數量：

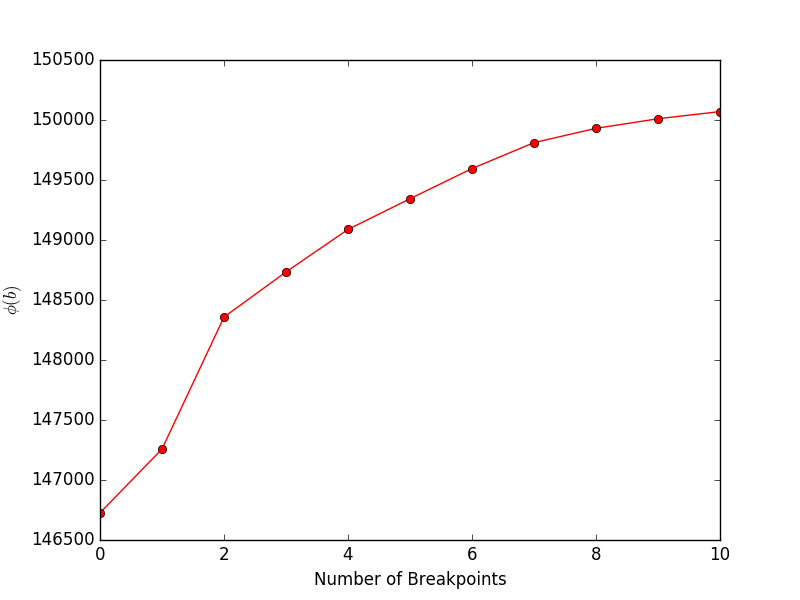
一旦我們解決了斷點的位置，我們就可以使用FindMeanCovs()函數來找出每個段落的平均值和協方差。在helloworld.py的範例中，繪製三個訊號的平均值、變異數和協方差得出：

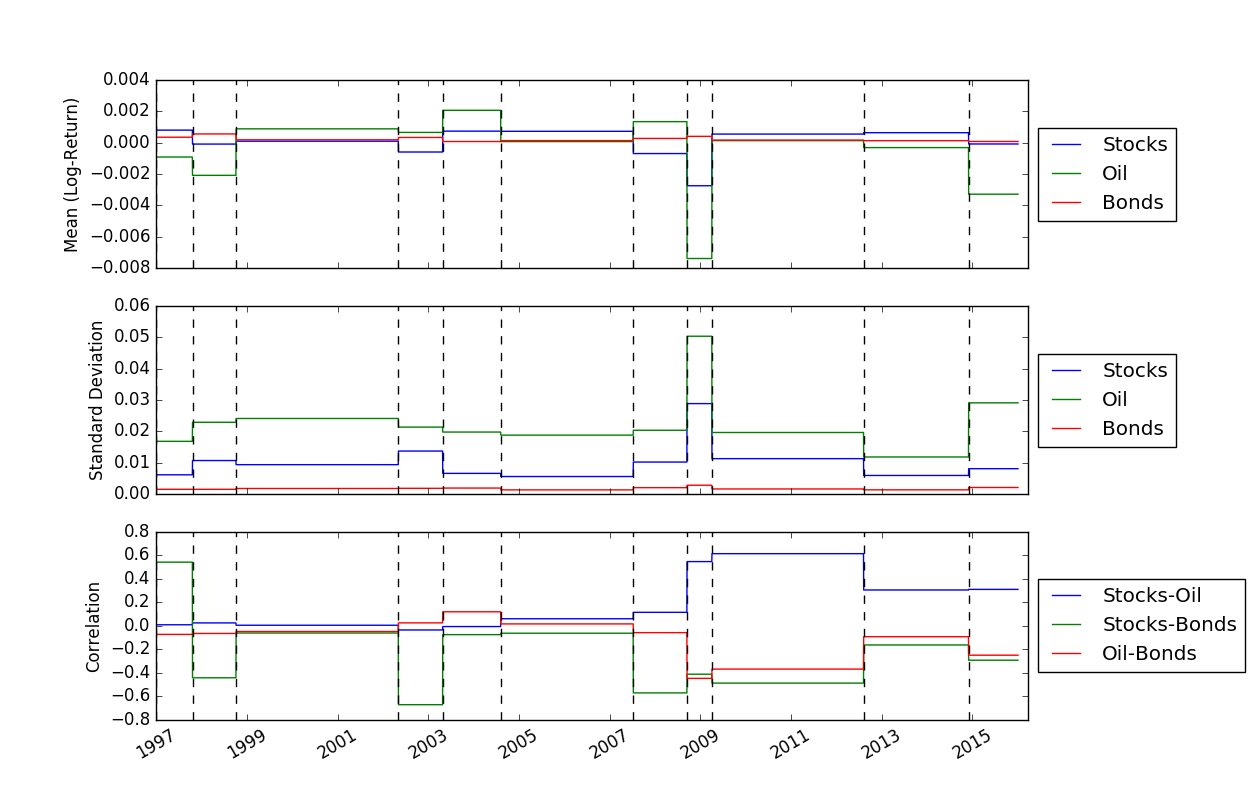
要運行交叉驗證（這對於確定 K 和 lambda 的最佳值非常有用），我們可以使用以下程式碼載入數據，運行交叉驗證，然後繪製測試和訓練似然：

 from ggs import *
import numpy as np
import matplotlib.pyplot as plt

filename = "Returns.txt"
data = np.genfromtxt(filename,delimiter=' ')
feats = [0,3,7]

#Run cross-validaton up to Kmax = 30, at lambda = 1e-4
maxBreaks = 30
lls = GGSCrossVal(data, Kmax=maxBreaks, lambList = [1e-4], features = feats, verbose = False)

trainLikelihood = lls[0][1][0]
testLikelihood = lls[0][1][1]
plt.plot(range(maxBreaks+1), testLikelihood)
plt.plot(range(maxBreaks+1), trainLikelihood)
plt.legend(['Test LL','Train LL'], loc='best')
plt.show()

結果圖如下圖所示：

參考

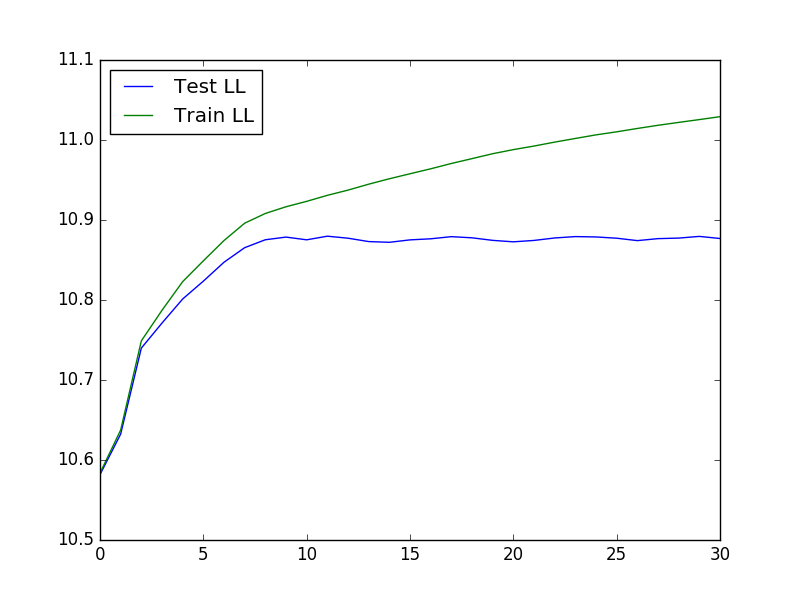
時間序列資料的貪婪高斯分割－D. Hallac、P. Nystrup 和 S. Boyd

作者

大衛哈拉克、彼得尼斯特魯普和史蒂芬博伊德。