greta.gam：使用 mgcv 的 greta 中的廣義加法模型

greta.gam 可讓您使用 mgcv 的平滑函數和公式語法來定義在 greta 模型中使用的平滑項。然後，您可以定義自己完成模型的可能性，並透過 MCMC 對其進行擬合。

這是正在進行中的工作！

例子

這是改編自mgcv ?gam幫助文件的簡單範例：

在mgcv ：

Gu & Wahba 4 term additive model # fit a model using gam() b <- gam(y ~ s(x2), data = dat)">

library( mgcv )
# > Loading required package: nlme
# > This is mgcv 1.9-1. For overview type 'help("mgcv-package")'.
set.seed( 2 )

# simulate some data...
dat <- gamSim( 1 , n = 400 , dist = " normal " , scale = 0.3 )
# > Gu & Wahba 4 term additive model

# fit a model using gam()
b <- gam( y ~ s( x2 ), data = dat )

現在在greta中擬合相同的模型：

NULL # plot the data points(dat$x2, dat$y, pch = 19, cex = 0.2)">

library( greta.gam )
# > Loading required package: greta
# > 
# > Attaching package: 'greta'
# > The following objects are masked from 'package:stats':
# > 
# >     binomial, cov2cor, poisson
# > The following objects are masked from 'package:base':
# > 
# >     %*%, apply, backsolve, beta, chol2inv, colMeans, colSums, diag,
# >     eigen, forwardsolve, gamma, identity, rowMeans, rowSums, sweep,
# >     tapply
set.seed( 2024 - 02 - 09 )
# setup the linear predictor for the smooth
z <- smooths( ~ s( x2 ), data = dat )
# > ℹ Initialising python and checking dependencies, this may take a moment.
# > ✔ Initialising python and checking dependencies ... done!               

# set the distribution of the response
distribution( dat $ y ) <- normal( z , 1 )

# make some prediction data
pred_dat <- data.frame ( x2 = seq( 0 , 1 , length.out = 100 ))

# z_pred stores the predictions
z_pred <- evaluate_smooths( z , newdata = pred_dat )

# build model
m <- model( z_pred )

# draw from the posterior
draws <- mcmc( m , n_samples = 200 )
# > running 4 chains simultaneously on up to 8 CPU cores
#>     warmup                                           0/1000 | eta:  ?s              warmup ==                                       50/1000 | eta: 30s              warmup ====                                    100/1000 | eta: 17s              warmup ======                                  150/1000 | eta: 12s              warmup ========                                200/1000 | eta: 10s              warmup ==========                              250/1000 | eta:  8s              warmup ===========                             300/1000 | eta:  7s              warmup =============                           350/1000 | eta:  6s              warmup ===============                         400/1000 | eta:  5s              warmup =================                       450/1000 | eta:  5s              warmup ===================                     500/1000 | eta:  4s              warmup =====================                   550/1000 | eta:  4s              warmup =======================                 600/1000 | eta:  3s              warmup =========================               650/1000 | eta:  3s              warmup ===========================             700/1000 | eta:  2s              warmup ============================            750/1000 | eta:  2s              warmup ==============================          800/1000 | eta:  1s              warmup ================================        850/1000 | eta:  1s              warmup ==================================      900/1000 | eta:  1s              warmup ====================================    950/1000 | eta:  0s              warmup ====================================== 1000/1000 | eta:  0s          
# >   sampling                                            0/200 | eta:  ?s            sampling ==========                                50/200 | eta:  1s            sampling ===================                      100/200 | eta:  0s            sampling ============================             150/200 | eta:  0s            sampling ======================================   200/200 | eta:  0s

# plot the mgcv fit
plot( b , scheme = 1 , shift = coef( b )[ 1 ])

# add in a line for each posterior sample
apply( draws [[ 1 ]], 1 , lines , x = pred_dat $ x2 , col = " blue " )
# > NULL

# plot the data
points( dat $ x2 , dat $ y , pch = 19 , cex = 0.2 )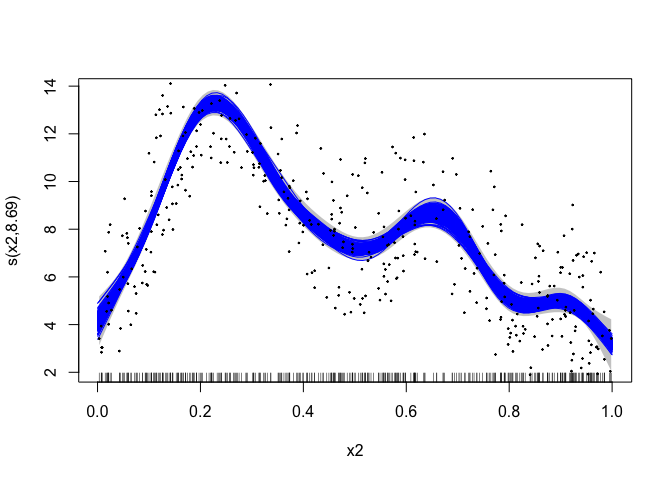

簡要技術細節

greta.gam使用mgcv中jagam (Wood, 2016) 例程中的一些技巧來讓事情正常運作。對於那些對內部運作感興趣的人來說，以下是一些簡短的細節...

GAM 的貝葉斯解釋

GAM 是具有貝葉斯解釋的模型（即使使用「頻率派」方法進行擬合）。人們可以將平滑懲罰矩陣視為貝葉斯隨機效應模型中的先驗精度矩陣。設計矩陣的建構與頻率論案例完全相同。有關這方面的更多背景信息，請參閱 Miller (2021)。

懲罰矩陣

GAM 的貝葉斯解釋有一點困難，因為在其樸素形式中，先驗作為懲罰的零空間（在一維情況下，通常是線性項）是不合適的。為了獲得正確的先驗，我們可以使用 Marra & Wood (2011) 中使用的「技巧」之一——即以某種方式懲罰導致不正確先驗的懲罰部分。我們採用jagam提供的選項，並為這些項創建一個額外的懲罰矩陣（來自懲罰矩陣的特徵分解；參見 Marra & Wood，2011）。