

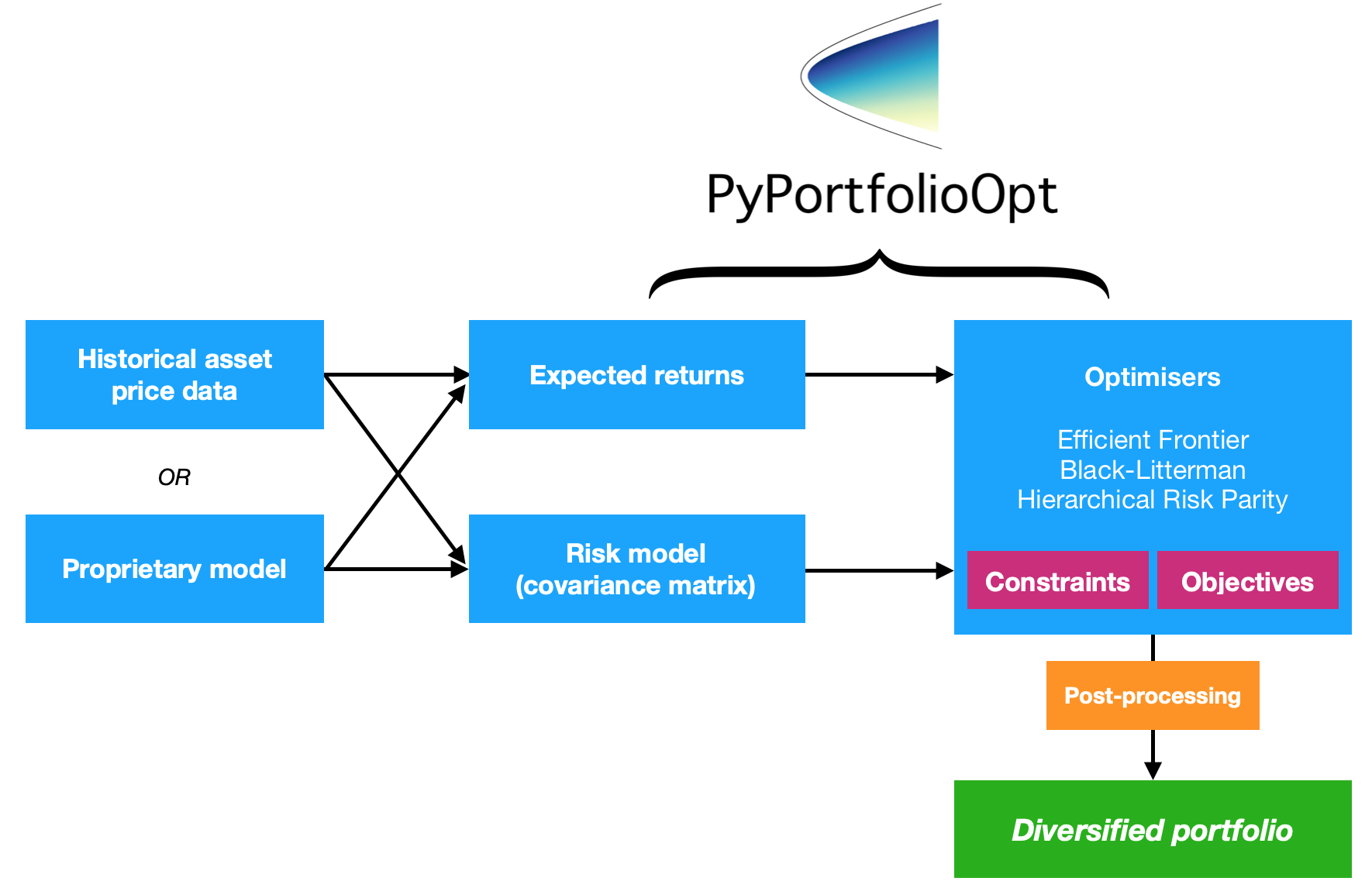
PyPortfolioOpt 是實現投資組合最佳化方法的函式庫,包括經典的平均值變異數最佳化技術和 Black-Litterman 分配,以及該領域的最新發展,例如收縮和分層風險平價。
它功能廣泛且易於擴展,對於休閒投資者或尋求簡單原型設計工具的專業人士來說都非常有用。無論您是一個以基本面為導向、已經確定了一些被低估的選擇的投資者,還是一個擁有一攬子策略的演算法交易者,PyPortfolioOpt 都可以幫助您以風險有效的方式組合您的阿爾法來源。
PyPortfolioOpt 已發表在《開源軟體雜誌》上?
PyPortfolioOpt 現在由 Tuan Tran 維護。
請造訪ReadTheDocs 上的文件以深入了解該項目,或查看說明書以查看一些範例,這些範例顯示了從下載資料到建立投資組合的完整過程。
如果您想在瀏覽器中以互動方式使用 PyPortfolioOpt,您可以在此處啟動 Binder。設定需要一段時間,但它可以讓您嘗試食譜,而不必處理所有要求。
注意:macOS 使用者需要安裝命令列工具。
注意:如果您使用的是 Windows,則首先需要安裝 C++。 (下載、安裝說明)
該項目可在 PyPI 上使用,這意味著您可以:
pip install PyPortfolioOpt(您可能需要遵循 cvxopt 和 cvxpy 的單獨安裝說明)。
但是,最佳實務是在虛擬環境中使用相依性管理器。我目前的建議是讓自己熟悉詩歌,然後就跑步
poetry add PyPortfolioOpt否則,克隆/下載項目並在專案目錄中運行:
python setup.py install PyPortfolioOpt 支援 Docker。使用docker build -f docker/Dockerfile . -t pypfopt 。您可以使用該映像來執行測試,甚至啟動 Jupyter 伺服器。
# iPython interpreter:
docker run -it pypfopt poetry run ipython
# Jupyter notebook server:
docker run -it -p 8888:8888 pypfopt poetry run jupyter notebook --allow-root --no-browser --ip 0.0.0.0
# click on http://127.0.0.1:8888/?token=xxx
# Pytest
docker run -t pypfopt poetry run pytest
# Bash
docker run -it pypfopt bash欲了解更多信息,請閱讀本指南。
如果您想進行重大更改以將其與您的專有系統集成,則克隆此存儲庫並僅使用原始程式碼可能是有意義的。
git clone https://github.com/robertmartin8/PyPortfolioOpt或者,您可以嘗試:
pip install -e git+https://github.com/robertmartin8/PyPortfolioOpt.git這是一個關於現實生活股票數據的範例,展示了找到最大化夏普比率(風險調整回報的衡量標準)的多頭投資組合是多麼容易。
import pandas as pd
from pypfopt import EfficientFrontier
from pypfopt import risk_models
from pypfopt import expected_returns
# Read in price data
df = pd . read_csv ( "tests/resources/stock_prices.csv" , parse_dates = True , index_col = "date" )
# Calculate expected returns and sample covariance
mu = expected_returns . mean_historical_return ( df )
S = risk_models . sample_cov ( df )
# Optimize for maximal Sharpe ratio
ef = EfficientFrontier ( mu , S )
raw_weights = ef . max_sharpe ()
cleaned_weights = ef . clean_weights ()
ef . save_weights_to_file ( "weights.csv" ) # saves to file
print ( cleaned_weights )
ef . portfolio_performance ( verbose = True )這會輸出以下權重:
{'GOOG': 0.03835,
'AAPL': 0.0689,
'FB': 0.20603,
'BABA': 0.07315,
'AMZN': 0.04033,
'GE': 0.0,
'AMD': 0.0,
'WMT': 0.0,
'BAC': 0.0,
'GM': 0.0,
'T': 0.0,
'UAA': 0.0,
'SHLD': 0.0,
'XOM': 0.0,
'RRC': 0.0,
'BBY': 0.01324,
'MA': 0.35349,
'PFE': 0.1957,
'JPM': 0.0,
'SBUX': 0.01082}
Expected annual return: 30.5%
Annual volatility: 22.2%
Sharpe Ratio: 1.28這很有趣,但本身並沒有什麼用處。然而,PyPortfolioOpt 提供了一種方法,可讓您將上述連續權重轉換為您可以購買的實際分配。只需輸入最新價格和所需的投資組合規模(本例為 10,000 美元):
from pypfopt . discrete_allocation import DiscreteAllocation , get_latest_prices
latest_prices = get_latest_prices ( df )
da = DiscreteAllocation ( weights , latest_prices , total_portfolio_value = 10000 )
allocation , leftover = da . greedy_portfolio ()
print ( "Discrete allocation:" , allocation )
print ( "Funds remaining: ${:.2f}" . format ( leftover ))12 out of 20 tickers were removed
Discrete allocation: {'GOOG': 1, 'AAPL': 4, 'FB': 12, 'BABA': 4, 'BBY': 2,
'MA': 20, 'PFE': 54, 'SBUX': 1}
Funds remaining: $ 11.89免責聲明:本項目不構成投資建議,作者對您後續的投資決策不承擔任何責任。請參閱許可證以獲取更多資訊。
Harry Markowitz 1952 年的論文是不可否認的經典,它將投資組合優化從一門藝術變成了一門科學。關鍵的見解是,透過將具有不同預期收益和波動性的資產組合起來,人們可以決定一種數學上的最優配置,從而最大限度地降低目標收益的風險——所有此類最優投資組合的集合被稱為有效前沿。
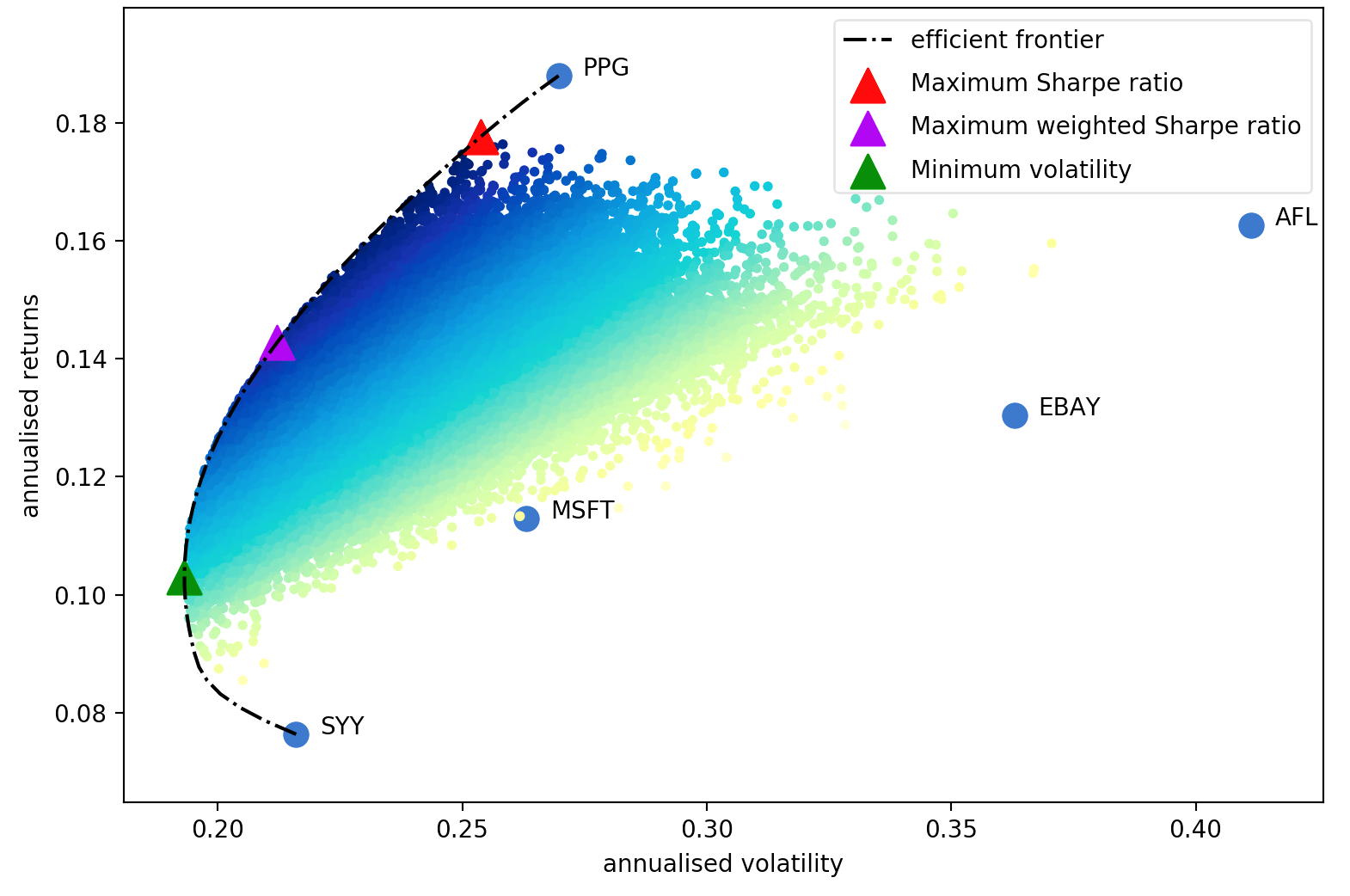
儘管這個主題已經取得了很大的發展,但半個多世紀後,馬科維茨的核心思想仍然具有根本性的重要意義,並且在許多投資組合管理公司中得到日常應用。平均值變異數最佳化的主要缺點是理論處理需要了解資產的預期收益和未來風險特徵(協方差)。顯然,如果我們知道股票的預期回報,生活會容易得多,但整個遊戲是股票回報很難預測。相反,我們可以根據歷史數據得出預期回報和協方差的估計——儘管我們確實失去了馬科維茨提供的理論保證,但我們的估計越接近實際值,我們的投資組合就越好。
因此,這個項目提供了四組主要的功能(儘管它們當然是密切相關的)
PyPortfolioOpt 的一個關鍵設計目標是模組化——使用者應該能夠交換其組件,同時仍使用 PyPortfolioOpt 提供的框架。
在本節中,我們將詳細介紹 PyPortfolioOpt 的一些可用功能。此處的 Jupyter 筆記本中提供了更多範例。另一個好的資源是測試。
可以在 ReadTheDocs 上找到更全面的版本,以及針對更高級用戶的可能擴充。
協方差矩陣不僅編碼資產的波動性,也編碼它與其他資產的相關性。這很重要,因為為了獲得多元化的好處(從而增加單位風險的回報),投資組合中的資產應盡可能不相關。
sklearn.covariance提供的高效向量化實現的包裝器。constant_variance 、 single_factor和constant_correlation 。sklearn.covariance中實現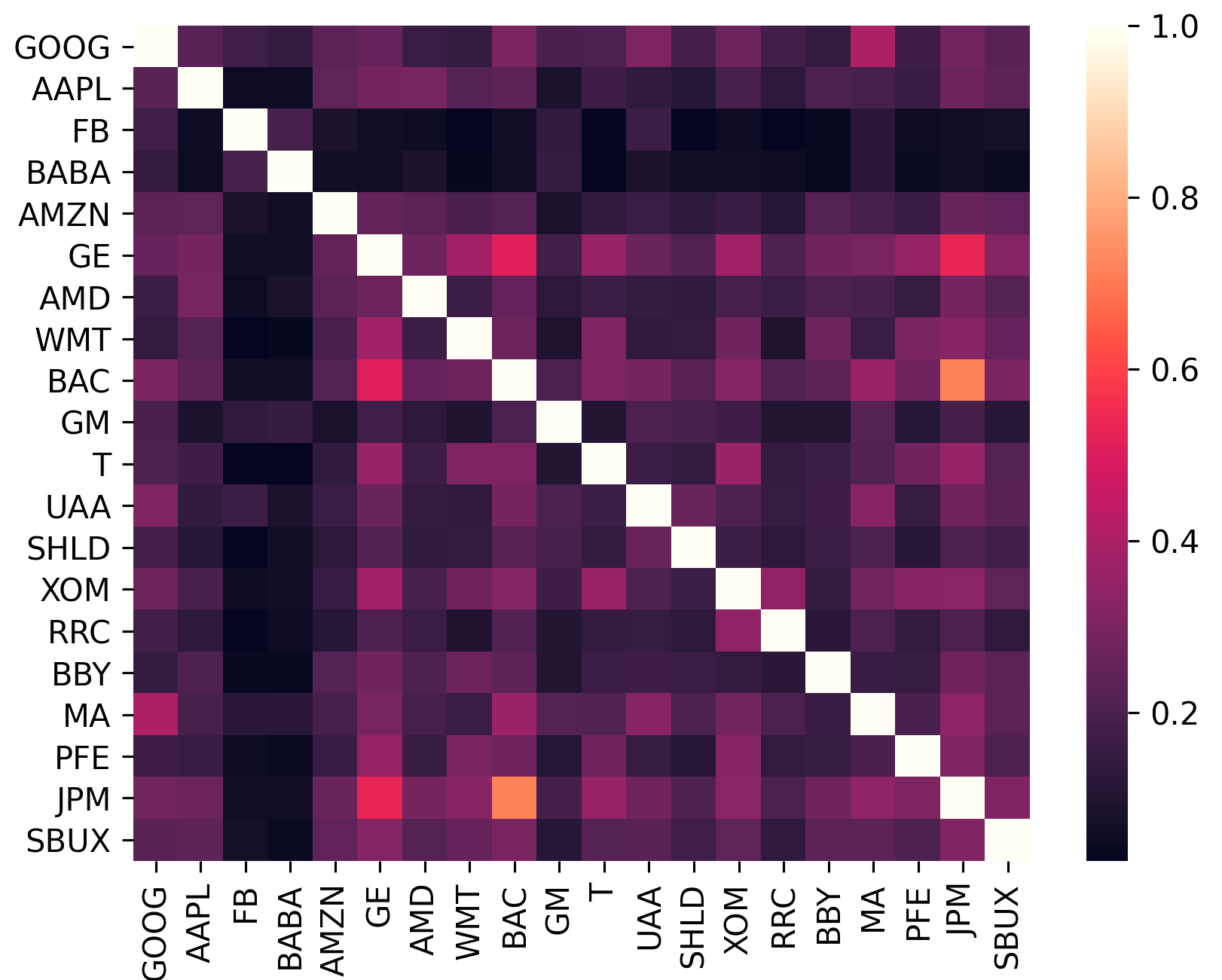
(該圖是使用plotting.plot_covariance產生的)
ef = EfficientFrontier ( mu , S , weight_bounds = ( - 1 , 1 ))efficient_risk和efficient_return方法,PyPortfolioOpt提供了形成市場中性投資組合的選項(即權重總和為零)。這對於最大夏普投資組合和最小波動率投資組合來說是不可能的,因為在這些情況下,它們對於槓桿而言不是不變的。市場中性需要負權重: ef = EfficientFrontier ( mu , S , weight_bounds = ( - 1 , 1 ))
ef . efficient_return ( target_return = 0.2 , market_neutral = True ) ef = EfficientFrontier ( mu , S , weight_bounds = ( 0 , 0.1 ))均值方差最佳化的一個問題是它會導致許多零權重。雖然這些在樣本內是「最佳」的,但大量研究表明,這項特徵導致平均值變異數投資組合的表現低於樣本外。為此,我引入了一個目標函數,它可以減少任何目標函數的可忽略權重的數量。本質上,它在小權重上添加了懲罰(由gamma參數化),這個術語看起來就像機器學習中的 L2 正則化。可能需要嘗試多個gamma值才能獲得所需數量的不可忽略的權重。對於 20 種證券的測試組合, gamma ~ 1就足夠了
ef = EfficientFrontier ( mu , S )
ef . add_objective ( objective_functions . L2_reg , gamma = 1 )
ef . max_sharpe ()從 v0.5.0 開始,我們現在支援 Black-Litterman 資產配置,它允許您將先前的回報估計(例如市場隱含回報)與您自己的觀點相結合,形成後驗估計。與僅使用平均歷史回報相比,這可以更好地估計預期回報。查看文件以取得理論討論以及有關格式化輸入的建議。
S = risk_models . sample_cov ( df )
viewdict = { "AAPL" : 0.20 , "BBY" : - 0.30 , "BAC" : 0 , "SBUX" : - 0.2 , "T" : 0.131321 }
bl = BlackLittermanModel ( S , pi = "equal" , absolute_views = viewdict , omega = "default" )
rets = bl . bl_returns ()
ef = EfficientFrontier ( rets , S )
ef . max_sharpe ()上述功能主要涉及透過二次規劃解決均值方差優化問題(儘管這是由cvxpy處理的)。但是,我們也提供不同的優化器:
請參閱文件以了解更多資訊。
測試是用 pytest 編寫的(在我看來,比unittest和變體更直觀),並且我試圖確保接近 100% 的覆蓋率。透過導航到套件目錄並簡單地在命令列上運行pytest來運行測試。
PyPortfolioOpt 提供了 20 隻股票每日收益的測試資料集:
[ 'GOOG' , 'AAPL' , 'FB' , 'BABA' , 'AMZN' , 'GE' , 'AMD' , 'WMT' , 'BAC' , 'GM' ,
'T' , 'UAA' , 'SHLD' , 'XOM' , 'RRC' , 'BBY' , 'MA' , 'PFE' , 'JPM' , 'SBUX' ]這些股票經過非正式選擇,以滿足以下幾個標準:
目前,測試尚未探索所有邊緣情況以及目標函數和參數的組合。然而,每種方法和參數都經過測試,可以按預期工作。
如果您使用 PyPortfolioOpt 來發表作品,請引用 JOSS 論文。
引文字串:
Martin, R. A., (2021). PyPortfolioOpt: portfolio optimization in Python. Journal of Open Source Software, 6(61), 3066, https://doi.org/10.21105/joss.03066
書目索引::
@article { Martin2021 ,
doi = { 10.21105/joss.03066 } ,
url = { https://doi.org/10.21105/joss.03066 } ,
year = { 2021 } ,
publisher = { The Open Journal } ,
volume = { 6 } ,
number = { 61 } ,
pages = { 3066 } ,
author = { Robert Andrew Martin } ,
title = { PyPortfolioOpt: portfolio optimization in Python } ,
journal = { Journal of Open Source Software }
}非常歡迎您的貢獻。請參閱貢獻指南以了解更多資訊。
我要感謝自 2018 年發布以來為 PyPortfolioOpt 做出貢獻的所有人員。