透過強化學習解決河內塔難題。
在安裝了 Numpy 和 Pandas 的 Python 環境中,執行腳本hanoi.py以產生結果部分中顯示的三個圖。例如,該腳本可以輕鬆地修改為使用不同數量的磁碟N來玩遊戲。
最近,隨著Google Deepmind 的 AlphaGo 擊敗了職業人類圍棋棋手,強化學習重新引起了人們的興趣。在這裡,一個更簡單的難題得到了解決:漢諾塔遊戲。此實作遵循 Watkins 和 Dayan [1] 最初提出的 Q 學習演算法。
河內塔遊戲由三個釘子和許多不同大小的可以滑到釘子上的圓盤組成。拼圖開始時,所有圓盤按升序堆疊在第一個釘子上,最大的在底部,最小的在頂部。遊戲的目標是將所有圓盤移動到第三個釘子。唯一合法的舉動是將最上面的圓盤從一個釘子移到另一個釘子上,但限制是永遠不能將一個圓盤放置在較小的圓盤上。圖 1 顯示了 4 個磁碟的最佳解決方案。

圖 1. 4 個圓盤的河內塔拼圖的動畫解決方案。 (資料來源:維基百科)。
遵循 Anderson [2],我們用元組表示遊戲的狀態,其中第 i個元素表示第i個磁碟位於哪個樁上。磁碟按大小遞增的順序進行標記。因此,初始狀態為 (111),所需的最終狀態為 (333)(圖 2)。
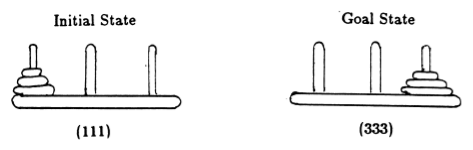
圖 2.具有 3 個圓盤的河內塔謎題的初始狀態和目標狀態。 (來自[2])。
謎題的狀態以及它們之間對應於合法移動的轉換形成了謎題的狀態轉換圖,如圖 3 所示。
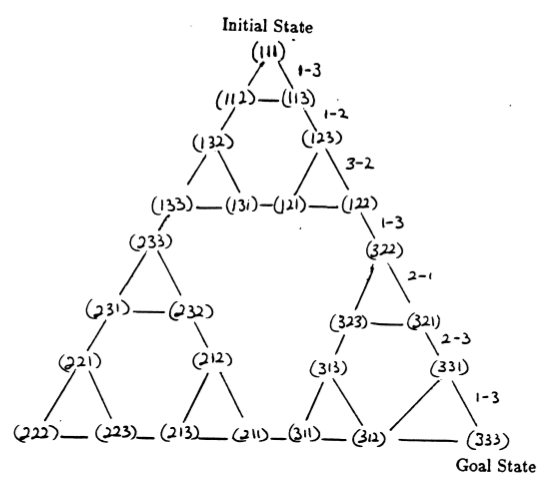
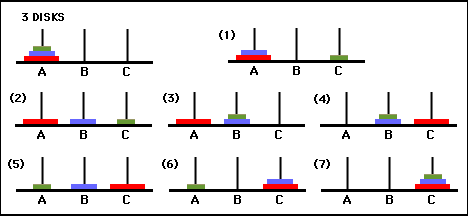
圖 3.三盤河內塔謎題的狀態轉換圖(上圖)和相應的最佳 7 步解(下圖),該解遵循圖右側的路徑。 (取自 [2] 和 Mathforum.org)。
解決漢諾塔謎題所需的最小移動次數為 2 N - 1,其中N是圓盤的數量。因此,對於N = 3,可以透過 7 次移動來解決這個難題,如圖 3 所示。
R和「行動價值」矩陣Q程式的第一步是產生一個獎勵矩陣R ,它捕獲遊戲規則並為獲勝者提供獎勵。為簡單起見,圖 4 中顯示了N = 2磁碟的獎勵矩陣。
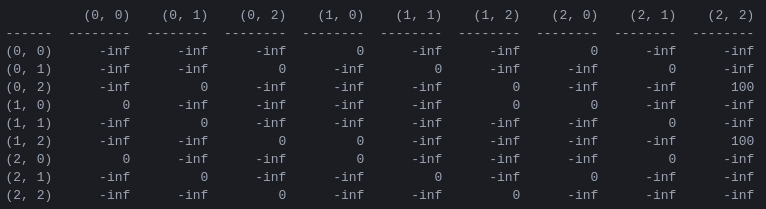
圖 4. N = 2圓盤的漢諾塔謎題的獎勵矩陣R第 ( i , j ) 個元素表示從狀態i移動到j的獎勵。狀態由元組標記,如圖2 和圖3 所示,不同之處在於,釘子以「Python 方式」索引,從0 到2,而不是從1 到3。會被分配獎勵為 100,非法走法為 ,所有其他走法為 0。
獎勵矩陣R僅描述即時獎勵:只有從倒數第二個狀態 (0,2) 和 (1,2) 才能獲得 100 的獎勵。在其他狀態下,2 或 3 種可能的移動中的每一種都有相同的獎勵 0,並且沒有明顯的理由選擇其中一種。
最終,我們尋求為每個狀態中的每個可能的移動分配一個“值”,以便透過最大化這些值,我們可以定義導致最佳解決方案的策略。每個狀態下每個動作的「值」矩陣稱為Q ,可以按照 Watkins 和 Dayan [1] 所描述的隨機方式遞歸求解或「學習」。 2 個磁碟的結果如圖 5 所示。
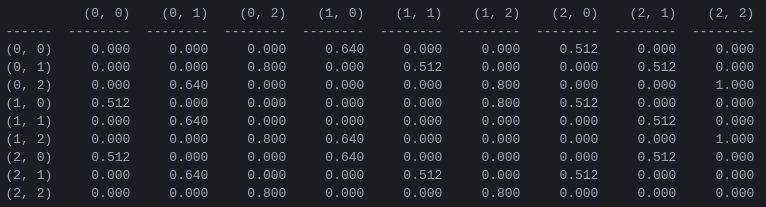
圖 5.具有 2 個圓盤的漢諾塔遊戲的「動作值」矩陣Q ,透過折扣因子 = 0.8、學習因子 = 1.0 和 1000 個訓練集進行學習。
矩陣Q的值本質上是可以分配給圖 3 中狀態轉換圖的頂點的權重,它引導智能體以盡可能短的方式從初始狀態到目標狀態。在此範例中,透過從狀態 (0,0) 開始並連續選擇具有最高Q值的移動,讀者可以確信Q矩陣引導智能體通過狀態序列 (0,0) - (1 ,0) - (1, 2) - (2,2),對應於2 盤漢諾塔遊戲的3 步最適解(圖6)。
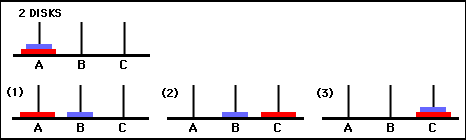
圖 6.使用 2 個圓盤的漢諾塔遊戲的解決方案。連續狀態分別以(0,0)、(1,0)、(1,2)和(2,2)表示。 (資料來源:mathforum.org)。
在此範例中,矩陣Q已收斂到其最優值,它定義了一個固定策略:每一行包含一個具有唯一最大值的操作。然而,在學習過程中,不同的動作可能具有相同的Q值。 (特別是,當Q初始化為零矩陣時,就是訓練開始時的情況)。在下一節介紹的模擬中,此類情況透過以下隨機策略處理:在多個操作之間共享最大 Q 值的情況下,隨機選擇這些操作之一。
Q 學習演算法的表現可以透過計算解決漢諾塔謎題所需的(平均)移動次數來衡量。這個數字隨著訓練次數的增加而減少,直到最終達到最佳值 2 N - 1,其中N是磁碟數量,如圖 7 所示,其中N = 2、3 和 4。
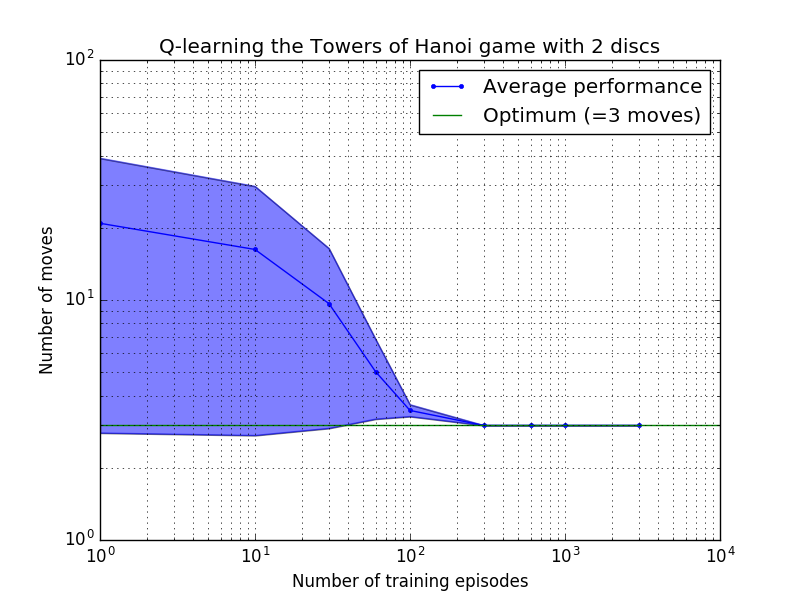
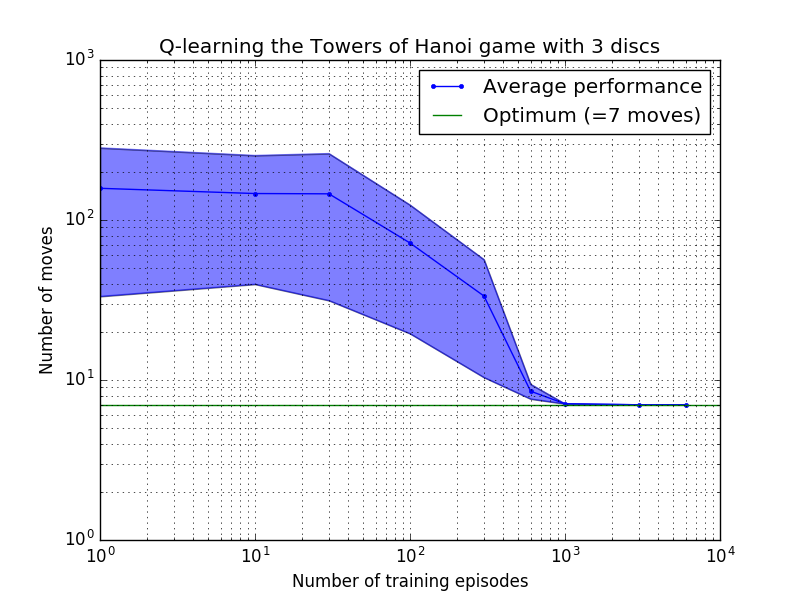
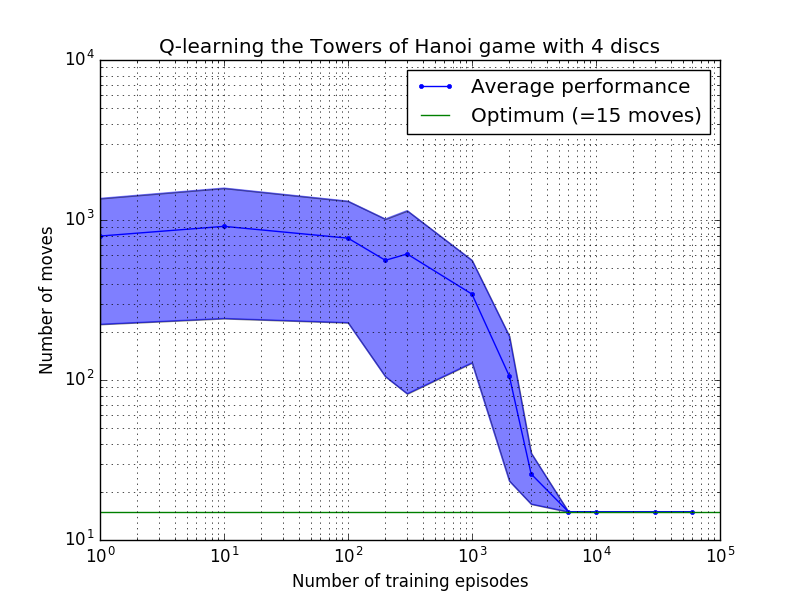
圖 7.漢諾塔遊戲的 Q 學習演算法的效能(從上到下依序為 2、3 和 4 個磁碟)。在所有情況下,學習都是以= 0.8 的折扣因子和= 1.0 的學習因子進行的。藍色實線代表每個產生的隨機策略經過 100 個 epoch 訓練和玩 100 次遊戲後的平均表現。藍色陰影區域的上限和下限與平均值的偏移量是估計的標準差。 (對於N = 3 和N = 4,由於計算限制,訓練次數和播放次數分別減少到 10 和 10)。
圖 7 中的學習特性的一個有趣特徵是,在所有情況下,學習最初都很慢,而且代理很難比隨機選擇動作的「零訓練」策略做得更好。在某個時刻,學習達到“拐點”,然後以加速的速度收斂到最佳移動次數(儘管這在對數尺度上有些誇大)。
Python 腳本透過 Q 學習成功地針對任意數量的磁碟成功解決了河內塔難題。該腳本可以輕鬆適應具有不同獎勵矩陣R其他問題。
收斂到最佳解決方案所需的訓練次數隨著磁碟數量N增加而大大增加:對於N=2磁碟,需要約 300 次訓練,而對於N=4則需要約 6,000 次訓練。學習演算法的一個可能的改進是允許它自動尋找遞歸解決方案,正如 Hengst [3] 所做的那樣。
[1] Watkins & Dayan, Q-learning ,機器學習,8, 279-292 (1992)。 (PDF)。
[2] Anderson,多層連接系統的學習和問題解決,博士。論文(1986)。 (PDF)。
[3] Hengst,以 HEXQ 發現強化學習的層次結構,第十九屆國際機器學習會議論文集(2002 年)。 (PDF)。