neurodiffeq

神經差分

引文

@article{chen2020neurodiffeq,
  title={NeuroDiffEq: A Python package for solving differential equations with neural networks},
  author={Chen, Feiyu and Sondak, David and Protopapas, Pavlos and Mattheakis, Marios and Liu, Shuheng and Agarwal, Devansh and Di Giovanni, Marco},
  journal={Journal of Open Source Software},
  volume={5},
  number={46},
  pages={1931},
  year={2020}
}

---

您是否知道 Neurodiffeq 支援解決方案套件並可用於解決反向問題？看這裡！

？已經熟悉 Neurodiffeq 了？ ？跳轉至常見問題。

---

介紹

neurodiffeq是用神經網路解微分方程式的套件。微分方程是將某些函數與其導數連結起來的方程式。它們出現在各個科學和工程領域。傳統上這些問題可以透過數值方法（例如有限差分、有限元素）來解決。雖然這些方法是有效且充分的，但它們的可表達性受到其函數表示的限制。如果我們能夠計算連續且可微的微分方程的解，那將會很有趣。

作為通用函數逼近器，人工神經網路已被證明具有求解具有某些初始/邊界條件的常微分方程 (ODE) 和偏微分方程 (PDE) 的潛力。 neurodiffeq的目標是實現使用 ANN 求解微分方程式的現有技術，使軟體足夠靈活，能夠處理各種使用者定義的問題。

安裝

使用點

與大多數標準庫一樣， neurodiffeq託管在 PyPI 上。要安裝最新的穩定版本，

 pip install -U Neurodiffeq # '-U' 表示更新至最新版本

手動

或者，您可以手動安裝該程式庫以儘早存取我們的新功能。對於想要為庫做出貢獻的開發人員，這是推薦的方式。

 git clone https://github.com/NeuroDiffGym/neurodiffeq.gitcd Neurodiffeq && pip install -r 要求
點安裝。  # 若要對庫進行更改，請使用 `pip install -e .`pytesttests/ # 執行測試。選修的。

入門

我們很樂意協助您解決任何問題。同時，您可以查看常見問題。

要查看neurodiffeq的完整教學和文檔，請查看官方文檔。

除了文件之外，我們最近還製作了帶有幻燈片的快速演練簡報影片。

用法範例

進口

從neurodiffeq導入diff從neurodiffeq.solvers導入Solver1D，Solver2D從neurodiffeq.conditions導入IVP，DirichletBVP2D從neurodiffeq.networks導入FCNN，SinActv

常微分方程系統範例

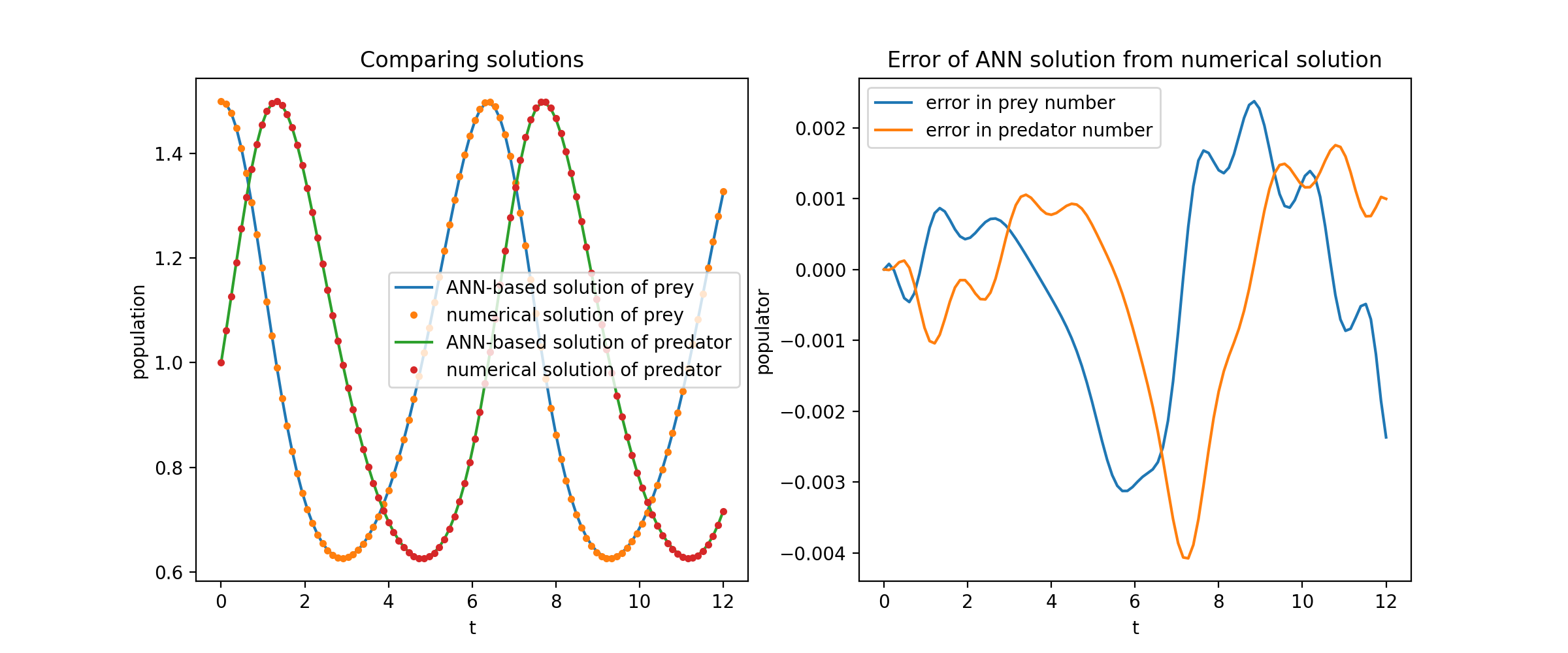
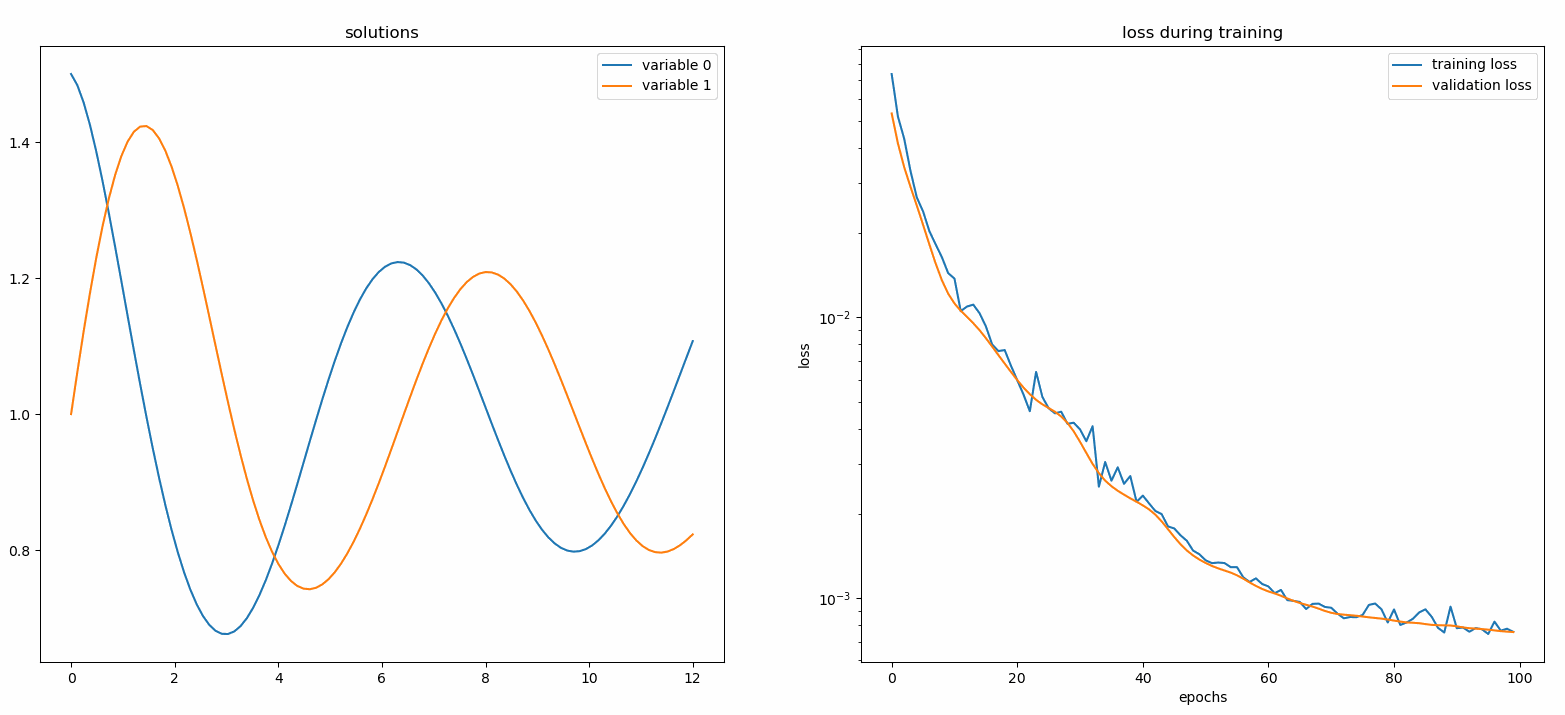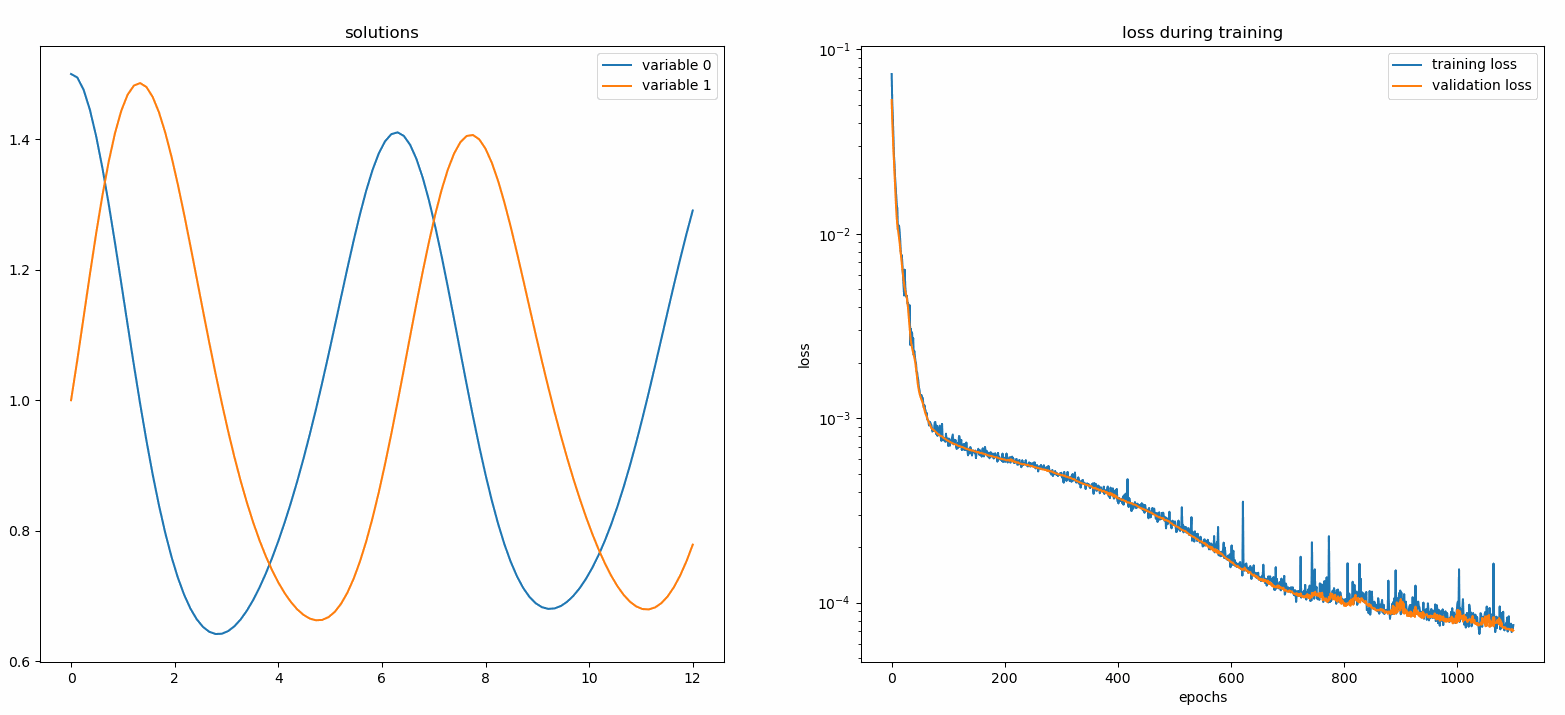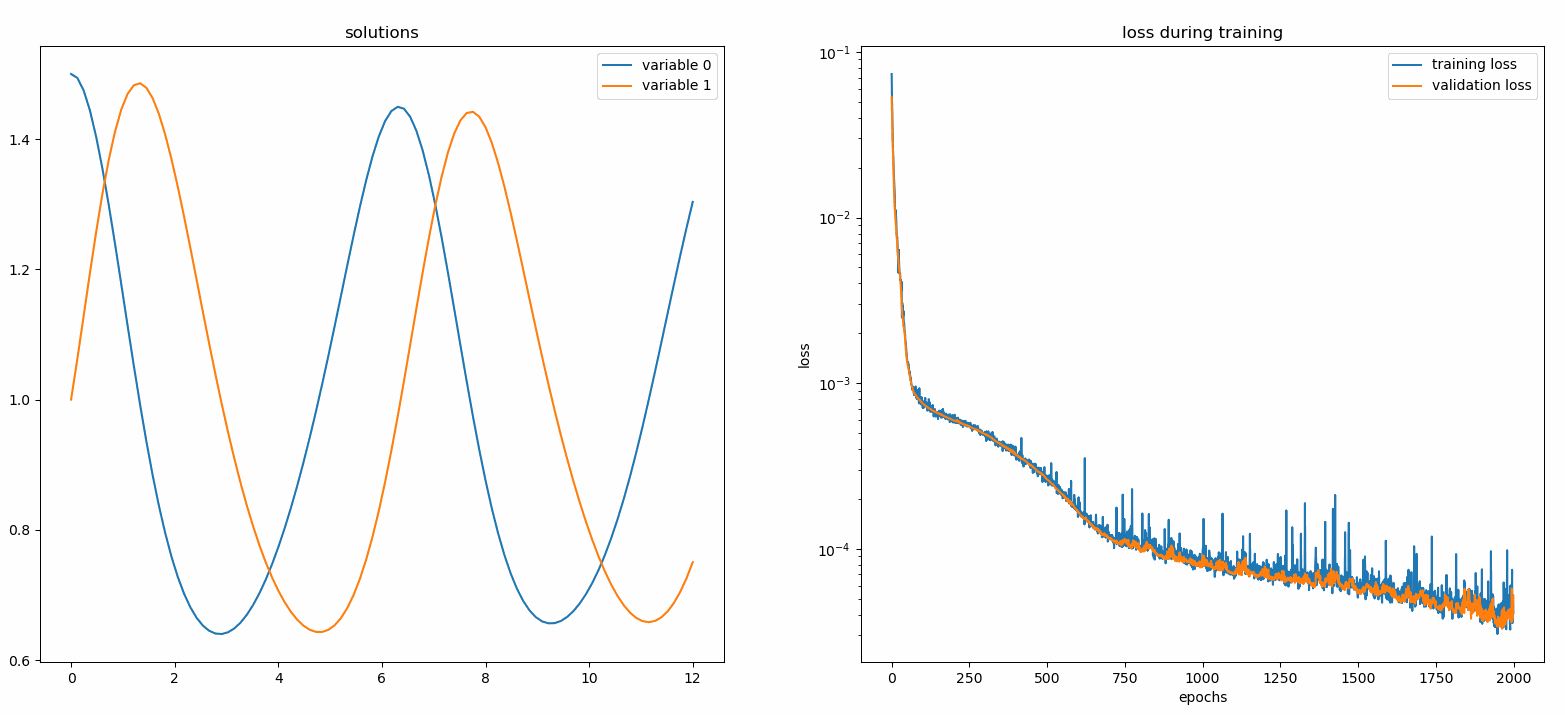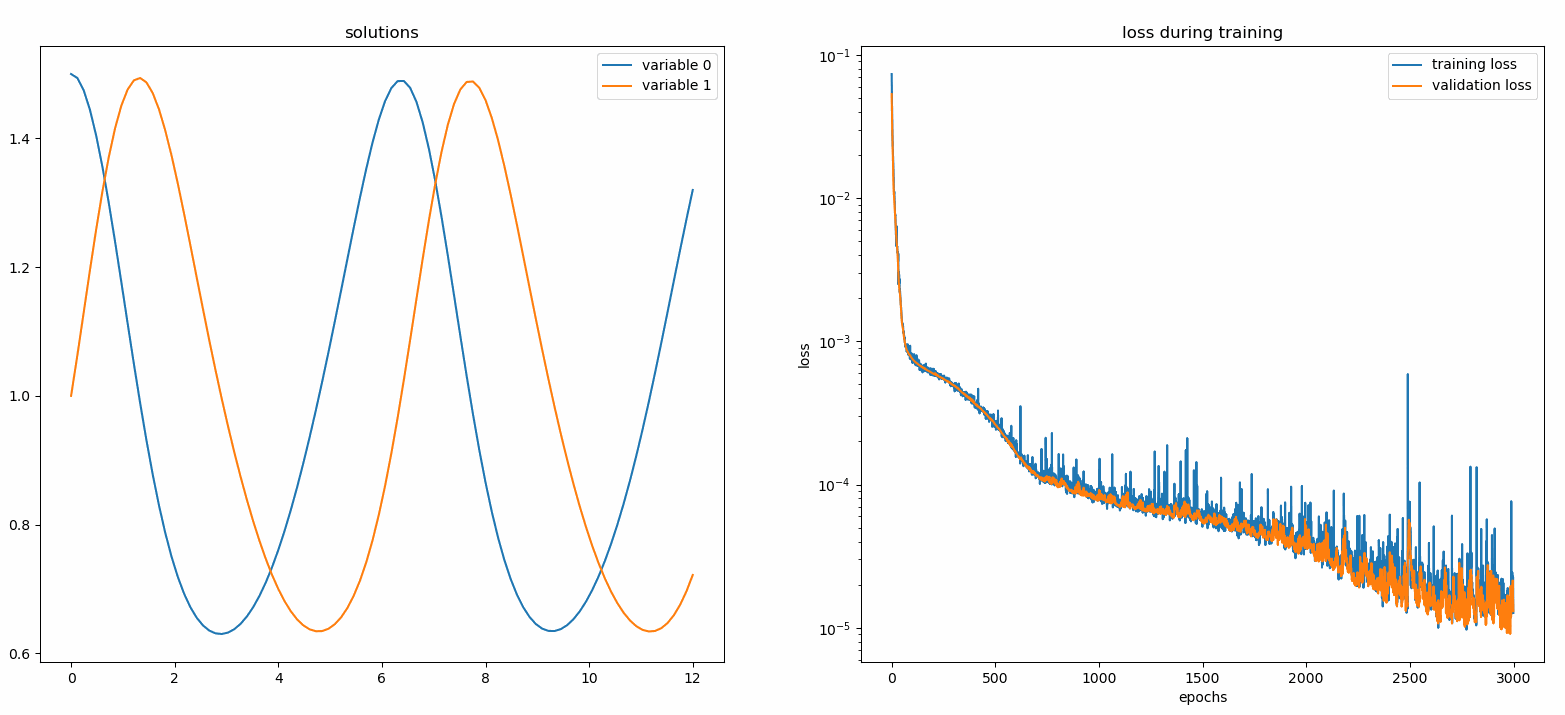
在這裡，我們求解兩個 ODE 的非線性系統，稱為 Lotka-Volterra 方程式。有兩個未知函數（ u和v ）和一個自變數（ t ）。

 def ode_system(u, v, t): 回傳[diff(u,t)-(uu*v), diff(v,t)-(u*vv)]條件= [IVP(t_0=0.0, u_0=1.5 ) ), IVP(t_0=0.0, u_0=1.0)]nets = [FCNN(actv=SinActv), FCNN(actv=SinActv)]求解器= Solver1D(ode_system, 條件, t_min=0.1, t_max=12.0, nets=12.0, nets=12.0, nets=12.0, nets=12.0, nets=12. nets) solver.fit(max_epochs=3000)solution =solver.get_solution()

solution是一個可調用對象，您可以將 numpy 數組或火炬張量傳遞給它，例如

u, v = Solution(t, to_numpy=True) # t 可以是 np.ndarray 或 torch.Tensor

將u和v相對於它們的解析解繪製出來，結果如下：

偏微分方程系統範例

在這裡，我們在矩形上求解具有狄利克雷邊界條件的拉普拉斯方程式。注意，我們選擇拉普拉斯方程式是因為它計算解析解的簡單性。在實踐中，只要您夠好地調整求解器，您就可以嘗試任何非線性、混沌偏微分方程。

求解 2-D PDE 系統與求解 ODE 非常相似，不同之處在於有兩個變數x和y （用於邊界值問題）或x和t （用於初始邊值問題），這兩個變數均受支持。

 def pde_system(u, x, y):回傳 [diff(u, x, order=2) + diff(u, y, order=2)]條件 = [DirichletBVP2D(x_min=0, x_min_val=lambda y: torch. sin(np.pi*y),x_max=1, x_max_val=lambda y: 0, y_min=0, y_min_val=lambda x: 0, y_max=1, y_max_val=lambda x: 0,
                       ）
]nets = [FCNN(n_input_units=2, n_output_units=1,hidden_​​units=(512,))]solver = Solver2D(pde_system, 條件, xy_min=(0, 0), xy_max=(1, 1), nets =nets) solver.fit(max_epochs=2000)solution =solver.get_solution()

二維偏微分方程的solution的簽名略有不同。同樣，它接受 numpy 陣列或 torch 張量。

 u = 解(x, y, to_numpy=True)

在[0,1] × [0,1]上計算 u 會得到以下圖

基於人工神經網路的解決方案	偏微分方程的殘差

使用顯示器

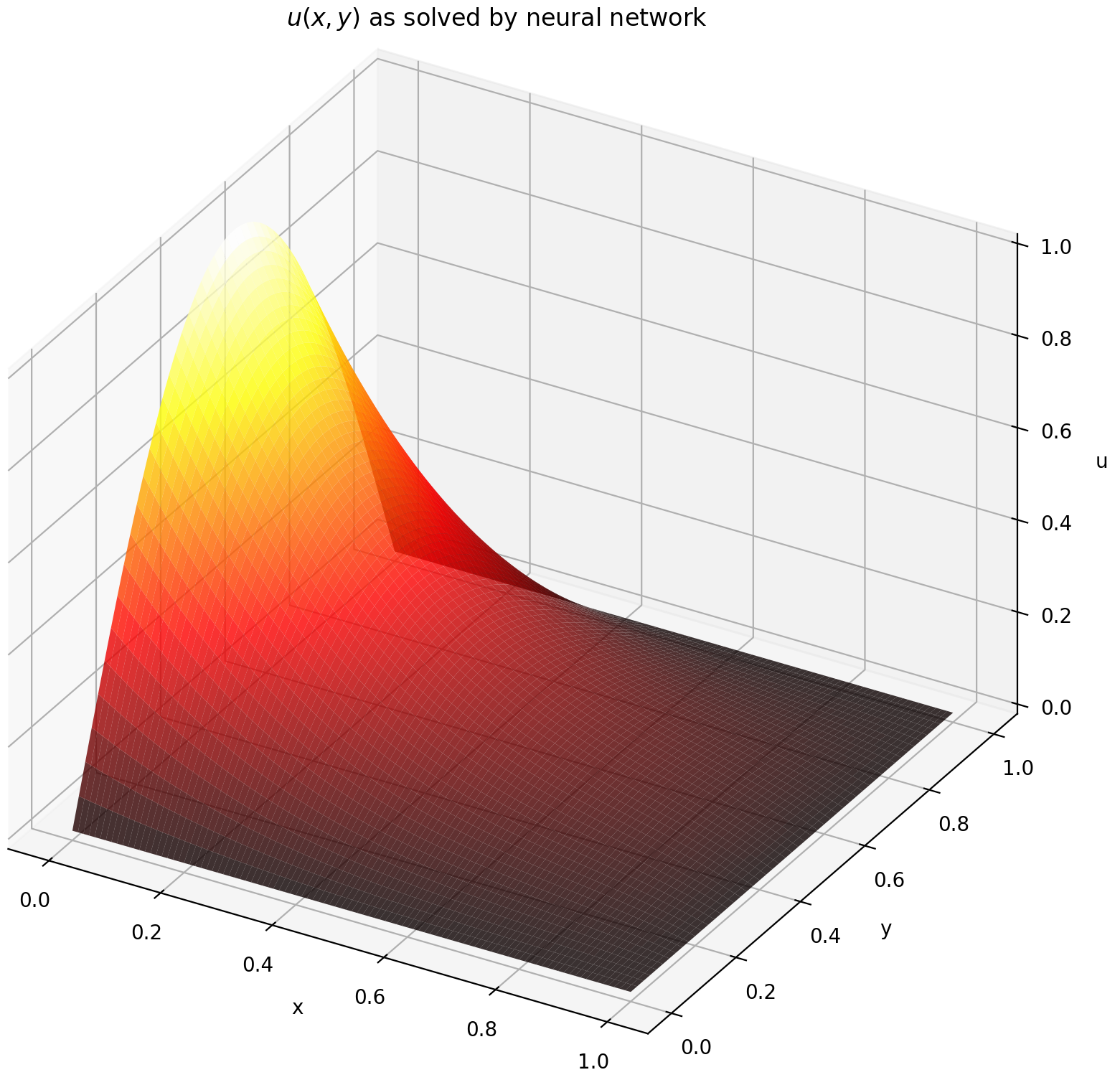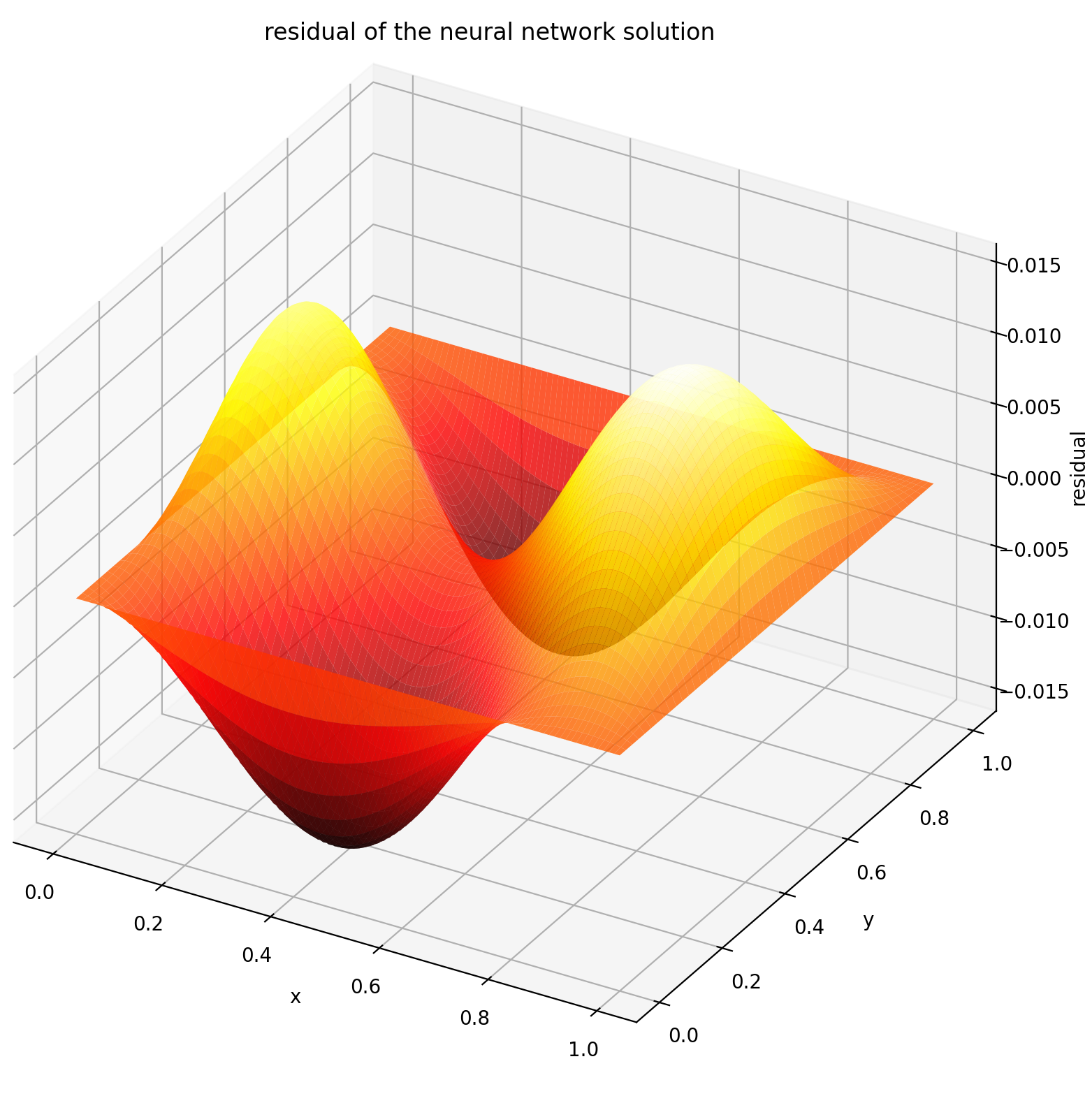監視器是一種用於可視化 PDE/ODE 解決方案以及訓練期間損失歷史和自訂指標的工具。 Jupyter Notebooks 使用者需要執行%matplotlib notebook魔法。對於 Jupyter Lab 用戶，請嘗試%matplotlib widget 。

從 Neurodiffeq.monitors 匯入 Monitor1D...monitor = Monitor1D(t_min=0.0, t_max=12.0, check_every=100)solver.fit(..., 回呼=[monitor.to_callback()])

您應該看到圖每 100 個 epoch以及最後一個 epoch更新一次，顯示兩個圖 - 一個用於區間[0,12]上的解決方案可視化，另一個用於損失歷史記錄（訓練和驗證）。

客製化網路

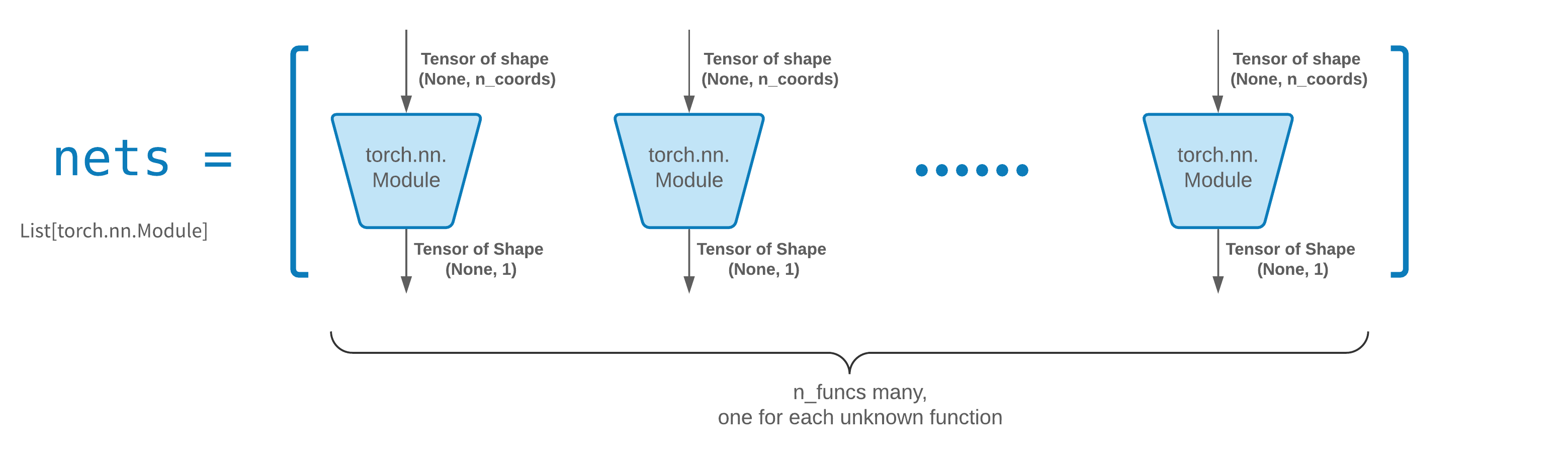
為了方便起見，我們實現了FCNN全連接神經網絡，其隱藏單元和激活函數可以定制。

 from Neurodiffeq.networks import FCNN# 預設：n_input_units=1, n_output_units=1,hidden_​​units=[32, 32],activation=torch.nn.Tanhnet1 = FCNN(n_input_units=..., n_out_units=... hidden_​​units=[ ..., ..., ...]，啟動=...)
 ...網路 = [net1, net2, ...]

FCNN通常是一個很好的起點。對於高級用戶，求解器與任何自訂torch.nn.Module相容。唯一的限制是：

1. 這些模組接受形狀為(None, n_coords)的張量，輸出形狀為(None, 1)的張量。

2. nets中必須總共有n_funcs模組才能傳遞給solver = Solver(..., nets=nets) 。

實際上， neurodiffeq有一個single_net功能，它不遵守上述規則，這裡不再介紹。

閱讀有關建立您自己的網路（也稱為模組）架構的 PyTorch 教學。

遷移學習

透過將old_solver.nets （火炬模組列表）序列化到磁碟，然後載入它們並傳遞給新的求解器，可以輕鬆完成遷移學習：

 old_solver.fit(max_epochs=...)# ... 將`old_solver.nets` 轉儲到磁碟# ... 從磁碟載入網絡，將它們儲存在某個`loaded_nets` 變數中new_solver = Solver(.. ., nets=loaded_nets )new_solver.fit(max_epochs=...)

我們目前正在研究包裝函數來保存/載入網路和求解器的其他內部變數。同時，您可以閱讀有關儲存和載入網路的 PyTorch 教學。

抽樣策略

在 Neurodiffeq 中，透過最小化在域中一組點上評估的損失（ODE/PDE 殘差）來訓練網路。每次都會對點進行隨機重新採樣。若要控制採樣點的數量、分佈和邊界域，您可以指定自己的訓練/驗證generator 。

 from Neurodiffeq.generators import Generator1D# 預設 t_min=0.0, t_max=1.0, method='uniform', Noise_std=Noneg1 = Generator1D(size=..., t_min=..., t_max=..., method=.. .,noise_std=...)g2 = Generator1D(size=...,t_min=...,t_max=...,method=...,noise_std=...)solver = Solver1D(..., train_generator=g1, valid_generator=g2)

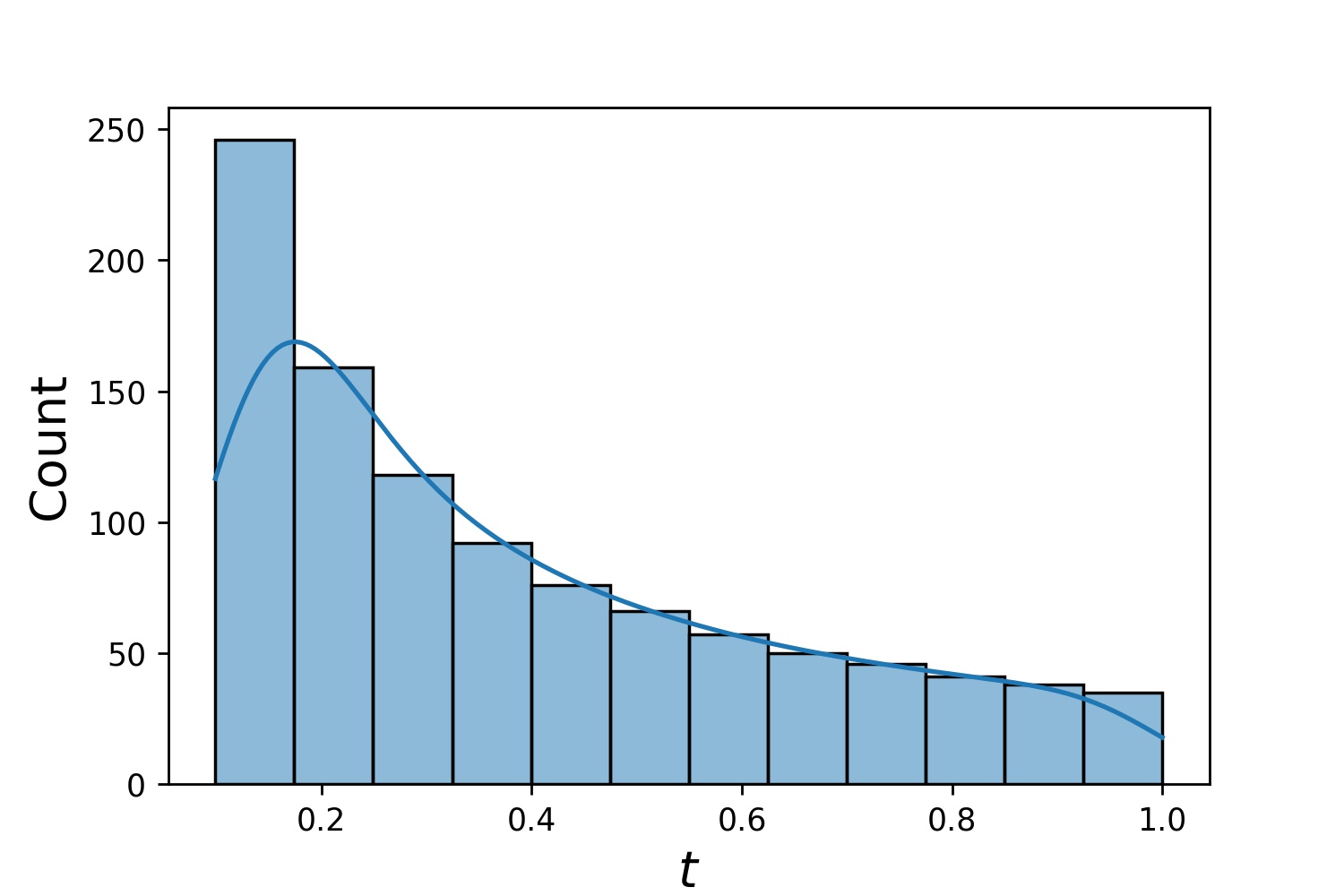
以下是Generator1D的一些範例分佈。

Generator1D(8192, 0.0, 1.0, method='uniform')	Generator1D(8192, -1.0, 0.0, method='log-spaced-noisy', noise_std=1e-3)

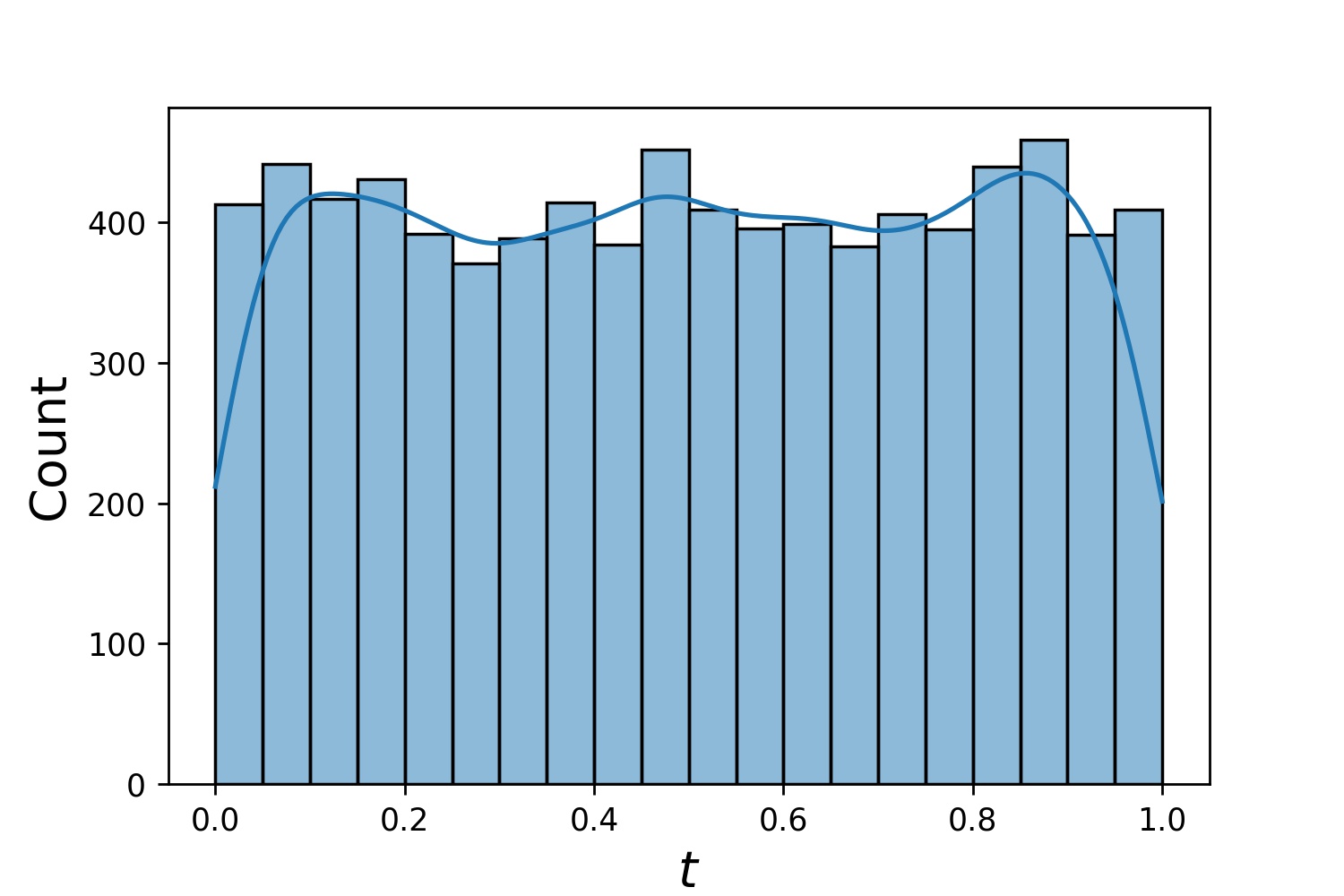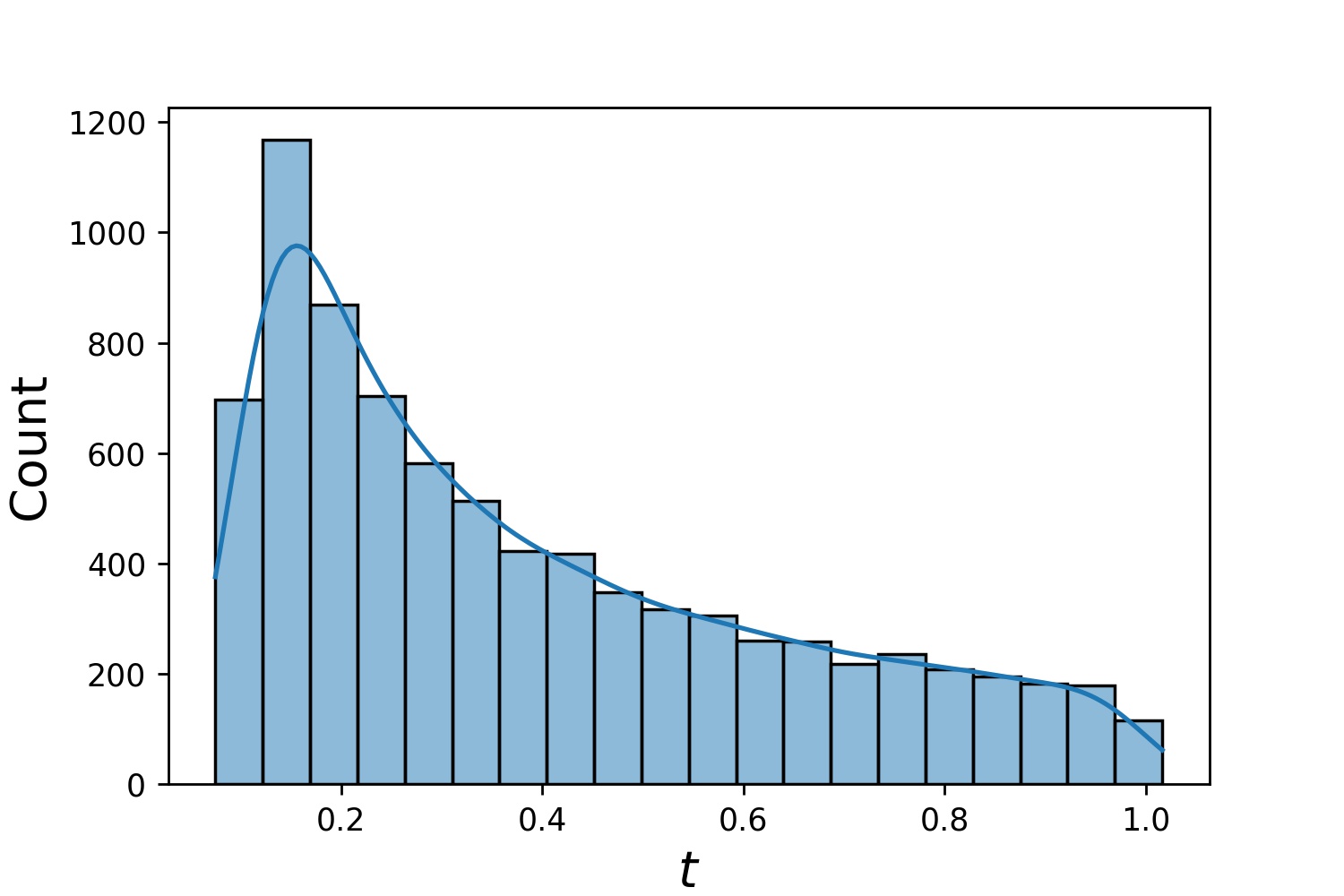注意，當同時指定train_generator和valid_generator時， Solver1D(...)中可以省略t_min和t_max 。事實上，即使你同時傳遞t_min 、 t_max 、 train_generator 、 valid_generator ， t_min和t_max仍然會被忽略。

組合發電機

生成器的另一個不錯的功能是您可以連接它們，例如

g1 = Generator2D((16, 16), xy_min=(0, 0), xy_max=(1, 1))g2 = Generator2D((16, 16), xy_min=(1, 1), xy_max=(2, 2 ) ))g = g1 + g2

這裡， g將是一個生成器，輸出g1和g2的組合樣本

g1	g2	g1 + g2

更高維度的取樣

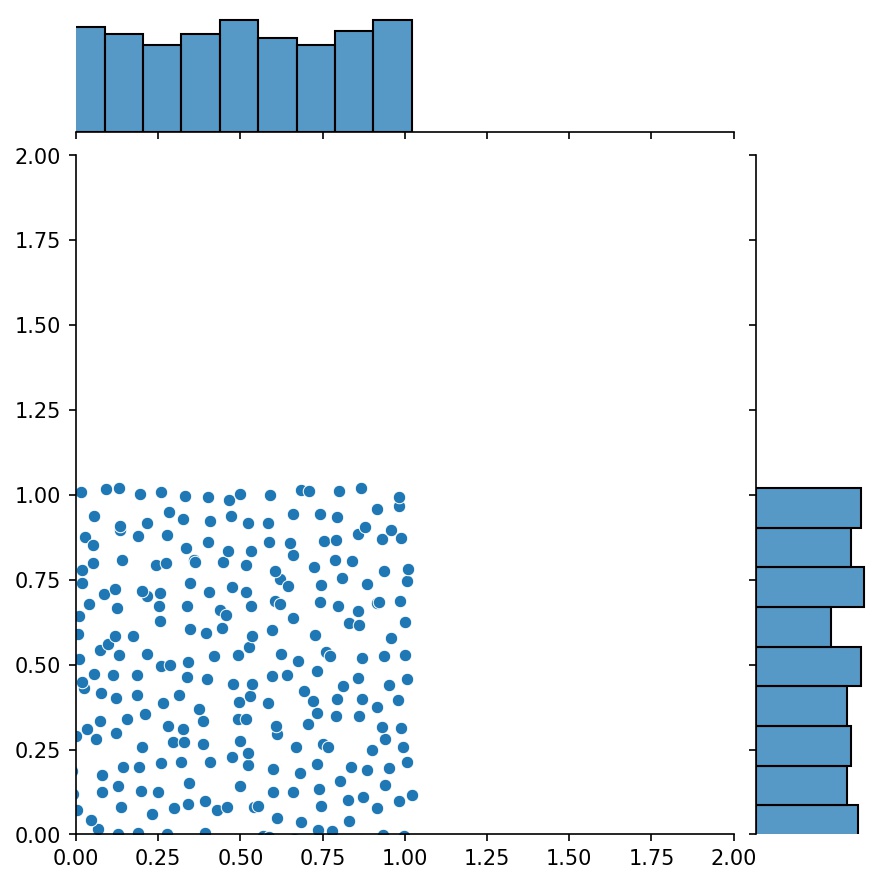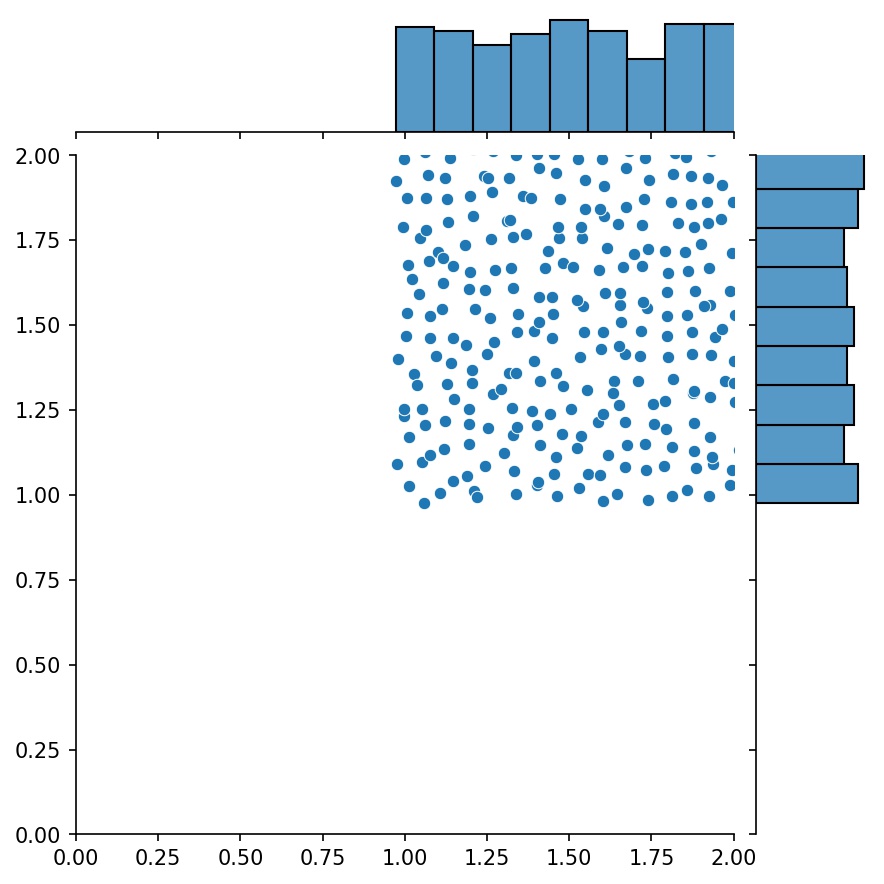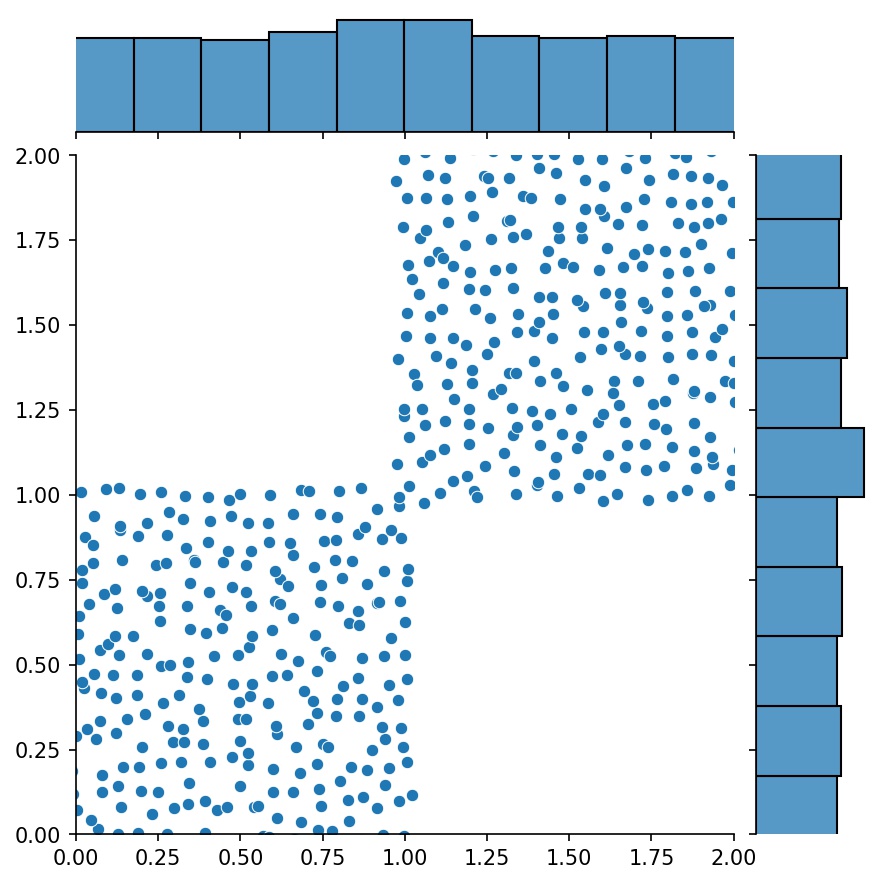您可以使用Generator2D 、 Generator3D等對更高維度的取樣點。但還有另一種方法

g1 = Generator1D(1024, 2.0, 3.0, method='uniform')g2 = Generator1D(1024, 0.1, 1.0, method='log-spaced-noisy',noise_std=0.001)g = g1 * g2spaced-noisy',noise_std=0.001)g = g1 * g2spaced

這裡， g將是一個生成器，每次在 2-D 矩形(2,3) × (0.1,1)中產生 1024 個點。它們的x座標是使用策略uniform從(2,3)繪製的，y座標是使用策略log-spaced-noisy從(0.1,1)繪製的。

g1	g2	g1 * g2

解決捆綁和逆向問題

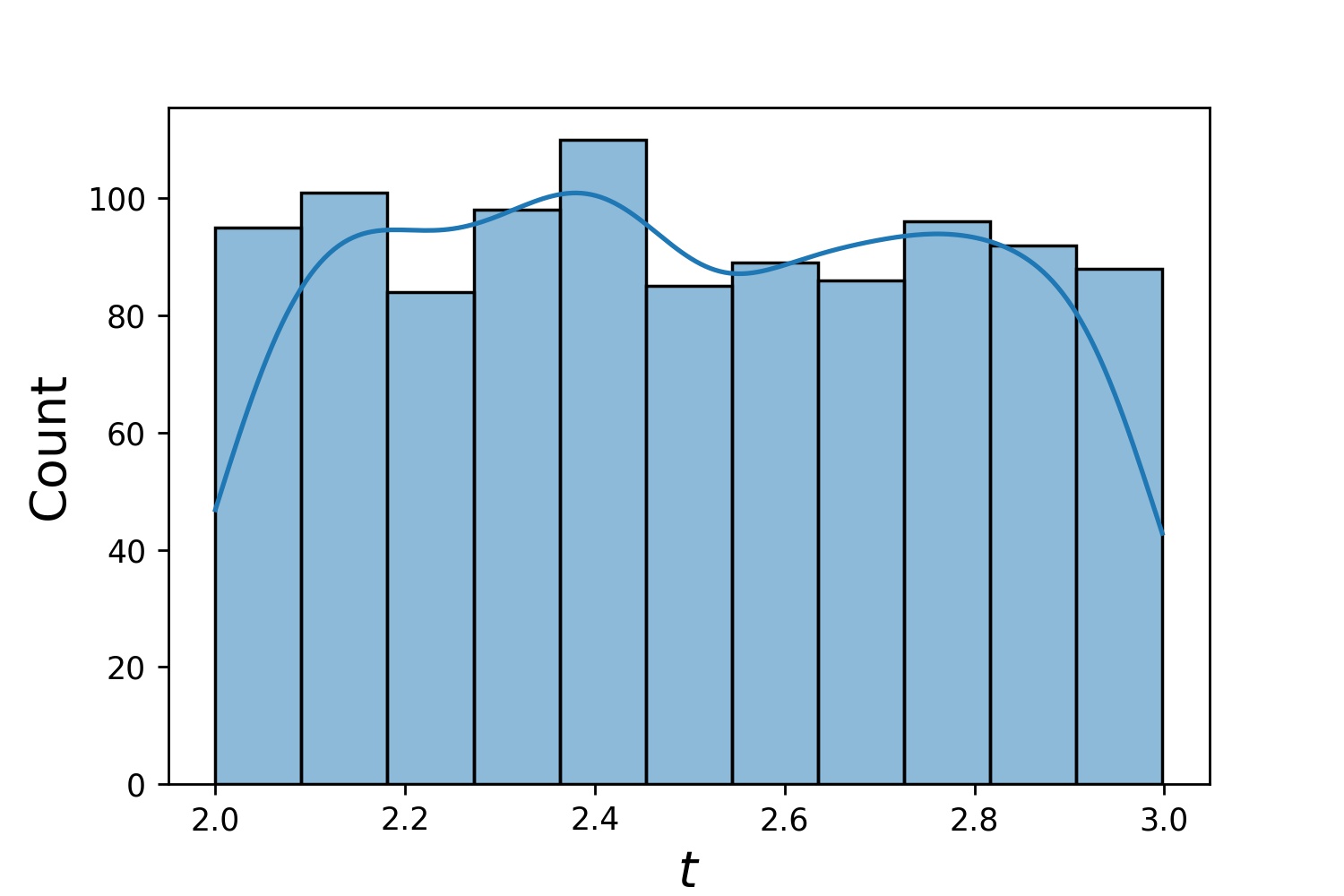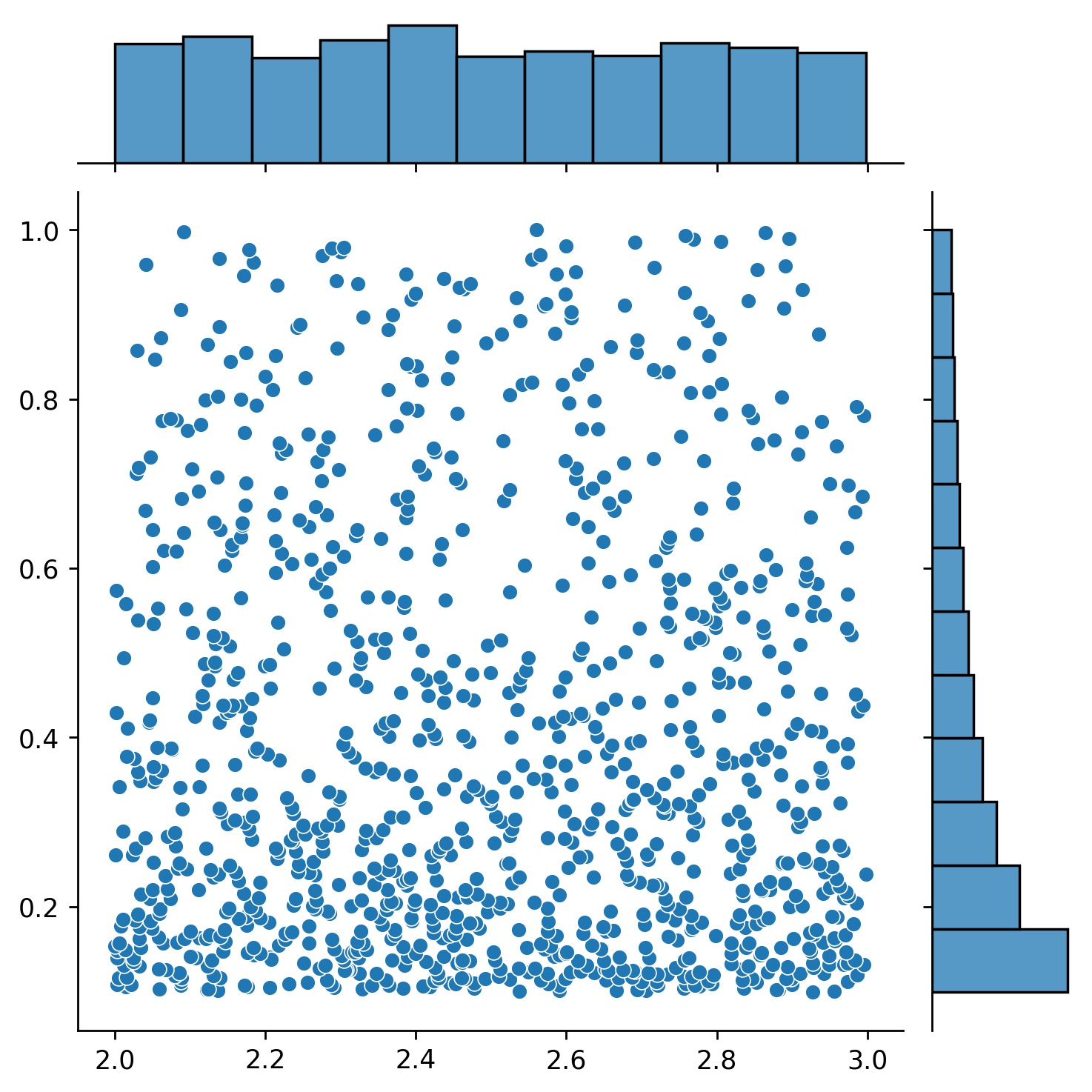有時，一次求解一組方程式是很有趣的。例如，您可能想要在初始條件u(0) = U0下求解du/dt + λu = 0形式的微分方程式。您可能希望透過將所有λ和U0視為神經網路的輸入來一次解決此問題。

其中一種應用是化學反應，其中反應速率未知。不同的反應速率對應不同的解決方案，並且只有一種解決方案與觀察到的數據點相符。您可能有興趣先求解一組解，然後確定最佳反應速率（也稱為方程式參數）。第二步稱為逆問題。

以下是如何使用neurodiffeq執行此操作的範例：

1. 假設我們有一個方程式du/dt + λu = 0和初始條件u(0) = U0 ，其中λ和U0是未知常數。我們還有一組觀察值t_obs和u_obs 。我們首先導入BundleSolver和BundleIVP這是獲取解決方案包所必需的：

   從neurodiffeq.conditions導入BundleIVP從neurodiffeq.solvers導入BundleSolver1D導入matplotlib.pyplot作為plt導入numpy作為np導入torch從neurodiffeq導入diff

2. 我們確定輸入t的域，以及參數λ和U0的域。我們還需要決定參數的順序。即，哪一個應該是第一個參數，哪一個應該是第二個參數。為本示範的目的，我們選擇λ作為第一個參數（索引 0），選擇U0作為第二個參數（索引 1）。追蹤參數的索引非常重要。

    T_MIN, T_MAX = 0, 1LAMBDA_MIN, LAMBDA_MAX = 3, 5 # 第一個參數，索引 = 0U0_MIN, U0_MAX = 0.2, 0.6 # 第二個參數，索引 = 1

3. 然後，我們像往常一樣定義conditions solver ，只是我們使用BundleIVP和BundleSolver1D而不是IVP和Solver1D 。這兩個的介面與IVP和Solver1D非常相似。您可以在 API 參考中了解更多。

    # 方程式參數位於輸入（通常是時間和空間座標）之後 diff_eq = lambda u, t, lmd: [diff(u, t) + lmd * u]# 關鍵字參數必須在 BundleIVP 中命名為「u_0」。如果你使用其他的東西，例如`y0`，`u0`等，它將不起作用。 index 1]solver = BundleSolver1D(ode_system=diff_eq,conditions=conditions,t_min=T_MIN, t_max=T_MAX, theta_min=[LAMBDA_MIN, U0_MIN], # λ 的索引為0；u_0 的索引為1theta_MAX=[0MBd # λ has index 0; u_0 has index 1eq_param_index=(0,), # λ 是唯一的方程式參數，其索引為 0n_batches_valid=1,
   ）

   由於λ是方程式中的參數， U0是初始條件中的參數，因此我們必須在diff_eq中包含λ ，在條件中包含U0 。如果某個參數同時出現在方程式和條件中，則必須將其包含在兩個位置中。傳遞給BundleSovler1D的所有conditions元素都必須是Bundle*條件，即使它們沒有參數。

4. 現在，我們可以像平常一樣訓練它並獲得解決方案。

    solver.fit(max_epochs=1000)solution =solver.get_solution(best=True)

   此解決方案需要三個輸入 - t 、 λ和U0 。所有輸入必須具有相同的形狀。例如，如果您有興趣固定λ=4和U0=0.4並繪製解u與t ∈ [0,1]關係，您可以執行下列操作

   t = np.linspace(0, 1)lmd = 4 * np.ones_like(t)u0 = 0.4 * np.ones_like(t)u = 解決方案(t, lmd, u0, to_numpy=True)導入matplotlib.pyplot 作為pltplt .plot(t, u)

5. 一旦有了捆綁solution ，您就可以找到一組與觀察到的資料點(t_i, u_i)最匹配的參數(λ, U0) 。這是使用簡單的梯度下降來實現的。在下面的玩具範例中，我們假設只有三個資料點u(0.2) = 0.273 、 u(0.5)=0.129和u(0.8) = 0.0609 。以下是經典的 PyTorch 工作流程。

    # 觀測資料點st_obs = torch.tensor([0.2, 0.5, 0.8]).reshape(-1, 1)u_obs = torch.tensor([0.273, 0.129, 0.0609]).reshape(-1, 1)隨機隨機隨機(#初始化λ 和 U0；追蹤它們的梯度lmd_tensor = torch.rand(1) * (LAMBDA_MAX - LAMBDA_MIN) + LAMBDA_MINu0_tensor = torch.rand(1) * (U0_MAX - U0_MIN) + U0_MINadam = torch.optim.Adam([dd_ten.relmue) u0_tensor.requires_grad_(True)], lr=1e-2)# 運行梯度下降10000 epochsfor _ in range(10000):output = Solution(t_obs, lmd_tensor * torch.ones_like(t_obsors), u0_ten) * ))loss = ((輸出- u_obs) ** 2).mean()loss.backward()adam.step()adam.zero_grad()
      print(f"λ = {lmd_tensor.item()}, U0={u0_tensor.item()}, 損失 = {loss.item()}")

常問問題

Q：如何使用GPU進行訓練？

簡單的。匯入 Neurodiffeq 時，庫會自動偵測 CUDA 在您的電腦上是否可用。由於該庫基於 PyTorch，因此如果找到相容的 GPU 設備，它將預設張量類型設為torch.cuda.DoubleTensor 。

Q：如何使用預訓練網路？

請參閱自訂網路和遷移學習部分。

Q：如何改變學習率？

標準 PyTorch 方式。

1. 依照自訂網路中的說明建構網路： nets = [FCNN(), FCN(), ...]

2. 實例化一個自訂優化器並將這些網路的所有參數傳遞給它

   parameters = [p for net in nets for p in net.parameters()] # 所有網路的參數清單MY_LEARNING_RATE = 5e-3optimizer = torch.optim.Adam(parameters, lr=MY_LEARNING_RATE, ...)

3. 將nets和optimizer傳遞給求解器： solver = Solver1D(..., nets=nets, optimizer=optimizer)

Q：我得到了一個糟糕的解決方案。

與傳統的數值方法（FEM、FVM 等）不同，基於神經網路的解決方案需要一些超級調整。該庫提供了最大的靈活性來嘗試任何超參數組合。

• 若要使用不同的網路架構，您可以傳入自訂的torch.nn.Module 。

• 要使用不同的最佳化器，您可以將自己的最佳化器傳遞給solver = Solver(..., optimizer=my_optim) 。

• 要使用不同的採樣分佈，您可以使用內建生成器或從頭開始編寫自己的生成器。

• 若要使用不同的取樣大小，您可以調整產生器或變更solver = Solver(..., n_batches_train) 。

• 若要在訓練期間動態變更超參數，請查看我們的回呼功能。

Q：有什麼經驗法則嗎？

• 不要使用ReLU進行激活，因為它的二階導數相同為 0。

• 以無量綱形式重新調整 PDE/ODE，最好讓所有內容都在[0,1]範圍內。使用像[0,1000000]這樣的域很容易失敗，因為a) PyTorch 將模組權重初始化得相對較小， b)大多數激活函數（如 Sigmoid、Tanh、Swish）在 0 附近最非線性。

• 如果您的 PDE/ODE 太複雜，請考慮嘗試課程學習。開始在較小的域上訓練網絡，然後逐漸擴展，直到覆蓋整個域。

貢獻

歡迎大家為這個專案做出貢獻。

在向該儲存庫做出貢獻時，我們考慮以下流程：

1. 打開一個問題來討論您計劃進行的更改。

2. 仔細閱讀貢獻指南。

3. 如果對介面進行了更改，請在分叉儲存庫上進行更改並更新 README.md。

4. 打開拉取請求。