Minimax AI 演算法在 Tic-Tac-Toe(或圈與叉)遊戲中的實現。試試:井字遊戲 - Minimax
為了使用人工智慧解決遊戲,我們將引入博弈樹的概念,然後引入極小極大演算法。遊戲的不同狀態由遊戲樹中的節點表示,與上面的規劃問題非常相似。這個想法只是略有不同。在遊戲樹中,節點按與遊戲中每個玩家的回合相對應的級別排列,因此樹的「根」節點(通常在圖的頂部描繪)是遊戲中的開始位置。在井字遊戲中,這將是尚未玩過 X 或 Os 的空網格。在根下的第二層,第一個玩家的移動可能會產生一些可能的狀態,無論是 X 還是 O。
第二層上的每個節點也將進一步將對手玩家的移動可以從其到達的狀態作為其子節點。如此下去,一層一層地進行,直到達到遊戲結束的狀態。在井字棋中,這意味著要么其中一個玩家獲得三併獲勝,要么棋盤已滿並且遊戲以平局結束。
Minimax 是一種應用於兩人遊戲的人工智慧,例如井字棋、西洋跳棋、西洋棋和圍棋。這種遊戲稱為零和遊戲,因為在數學表示中:一個玩家獲勝(+1),另一個玩家失敗(-1)或任何一方都沒有獲勝(0)。
此演算法遞歸地搜尋導致Max玩家獲勝或不輸(平手)的最佳走法。它考慮遊戲的當前狀態以及該狀態下的可用動作,然後對於它所玩的每個有效動作(交替min和max ),直到找到最終狀態(獲勝、平局或失敗)。
Algorithms in a Nutshell(George Heineman;Gary Pollice;Stanley Selkow,2009)一書對此演算法進行了研究。偽代碼(改編):
minimax(state, depth, player)
if (player = max) then
best = [null, -infinity]
else
best = [null, +infinity]
if (depth = 0 or gameover) then
score = evaluate this state for player
return [null, score]
for each valid move m for player in state s do
execute move m on s
[move, score] = minimax(s, depth - 1, -player)
undo move m on s
if (player = max) then
if score > best.score then best = [move, score]
else
if score < best.score then best = [move, score]
return best
end
現在我們將透過 Python 實作來了解該偽代碼的每個部分。 Python 實作可在此儲存庫中找到。首先,考慮一下:
棋盤 = [ [0, 0, 0], [0, 0, 0], [0, 0, 0] ]
最大值=+1
最小值=-1
MAX 可以是 X 或 O,MIN 可以是 O 或 X,無論如何。棋盤尺寸為 3x3。
def minimax ( state , depth , player ): if player == MAX :
return [ - 1 , - 1 , - infinity ]
else :
return [ - 1 , - 1 , + infinity ]兩位玩家都以你的最差成績開始。如果玩家是 MAX,則其得分為 -無窮大。否則,如果玩家是 MIN,則得分為+無限大。注意:無窮大是 inf 的別名(來自 Python 中的數學模組)。
棋盤上的最佳棋步是 [-1, -1](行和列)。
if depth == 0 or game_over ( state ):
score = evaluate ( state )
return score如果深度為零,則棋盤上沒有新的空白單元格可供玩。或者,如果玩家獲勝,則遊戲以 MAX 或 MIN 結束。因此將傳回該狀態的分數。
現在我們將看到包含遞歸的程式碼的主要部分。
for cell in empty_cells ( state ):
x , y = cell [ 0 ], cell [ 1 ]
state [ x ][ y ] = player
score = minimax ( state , depth - 1 , - player )
state [ x ][ y ] = 0
score [ 0 ], score [ 1 ] = x , y對於每個有效的移動(空單元格):
棋盤上的移動(+1 或 -1)被撤銷,行、列被收集。
下一步是將分數與最佳分數進行比較。
if player == MAX :
if score [ 2 ] > best [ 2 ]:
best = score
else :
if score [ 2 ] < best [ 2 ]:
best = score對於MAX玩家,將獲得更大的分數。對於 MIN 玩家,將獲得較低的分數。最後,返回最好的棋步。最終演算法:
def minimax ( state , depth , player ):
if player == MAX :
best = [ - 1 , - 1 , - infinity ]
else :
best = [ - 1 , - 1 , + infinity ]
if depth == 0 or game_over ( state ):
score = evaluate ( state )
return [ - 1 , - 1 , score ]
for cell in empty_cells ( state ):
x , y = cell [ 0 ], cell [ 1 ]
state [ x ][ y ] = player
score = minimax ( state , depth - 1 , - player )
state [ x ][ y ] = 0
score [ 0 ], score [ 1 ] = x , y
if player == MAX :
if score [ 2 ] > best [ 2 ]:
best = score
else :
if score [ 2 ] < best [ 2 ]:
best = score
return best 下面,最佳移動位於中間,因為最大值位於左側第二個節點。
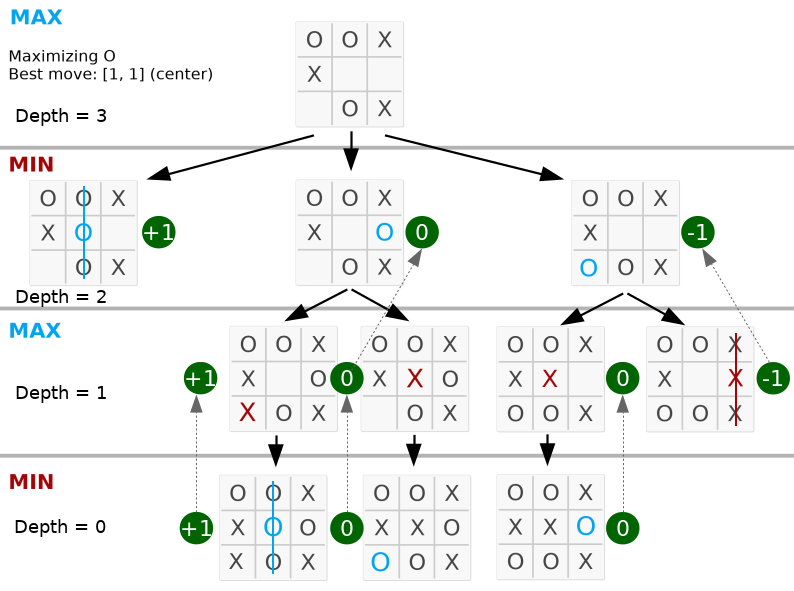
看看深度是否等於棋盤上的有效移動。完整的程式碼可以在py_version/中找到。
簡化的博弈樹:
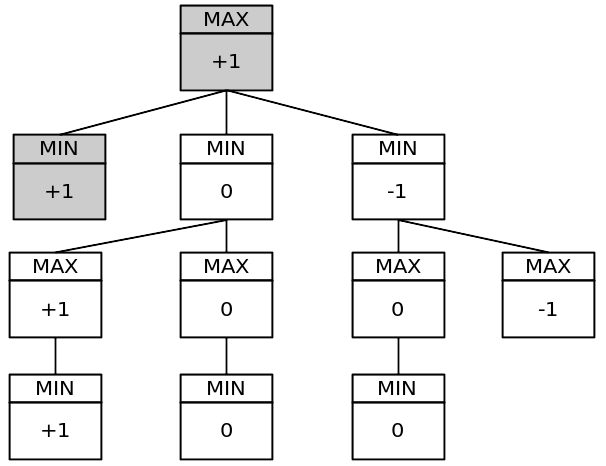
該樹有 11 個節點。完整的博弈樹有 549.946 個節點!您可以測試它,在程式中放置一個靜態全域變量,並為每輪的每個 minimax 函數呼叫遞增它。
在更複雜的遊戲中,例如國際象棋,很難搜尋整個遊戲樹。然而,Alpha-beta剪枝是極小極大演算法的一種最佳化方法,它允許我們忽略搜尋樹中的一些分支,因為他在搜尋中剪掉了不相關的節點(子樹)。有關更多信息,請參閱: