Rubik的Cube求解器,用於非常大的立方體。
求解從1到65536的任何大小的任何立方體。可以輕鬆修改代碼以處理更大的立方體。但是,主要的限制是系統上的內存量以及解決的時間長度。求解時間增長了〜n^2,這意味著要在每個維度中求解大2倍的立方體需要4-5倍。
1024個分層的立方體可以在約1.5秒內解決。大約20分鐘內可以解決16384分層的立方體。
YouTube:求解65536層YouTube:求解32768層
32768立方體前面的圖像
解決中心,然後邊緣邊緣
中心在15個階段解決,每個階段將某些顏色的所有碎片從一個臉部移動到所需的臉部。例如:一個階段將白色臉上的所有綠色碎片移到綠色的臉上。重複所有顏色和麵孔。
求解器使用此處描述的換向器,該換向器可以將中心碎片從一個臉部的一個像限到另一個臉上的震撼力。該換向器的一個非常重要的屬性是可以修改以同時將許多零件移動。對於非常大的立方體,這意味著它可以在一次操作中移動數百件甚至數千件。 k =(2 * p + 5) / p的平均移動數是p是可以移動每個操作的零件數。隨著立方體尺寸的增加,K迅速接近2。
使用基本的蠻力方法來解決角落,以將角移動到位,然後旋轉直到正確定向。威爾·史密斯(Will Smith
通過將每對邊緣移動到前面,然後從左邊緣到右邊緣交換所需的碎片來解決邊緣。需要解決或防止奇偶校驗問題的許多功能。
面部旋轉基本上是免費的。求解器沒有將所有片段(n^2片)移動到旋轉上,而是更改用於讀/寫入面的坐標系。這樣可以節省大量數據交換。
// Virtually rotate this face by q * 90 degrees
inline void Face::RotatefaceCW ( const int q)
{
orientation = (orientation + q) & 3 ;
}
// Gets the value of this face at coordinates r = row, c = column
inline const byte Face::GetRC ( const uint r, const uint c) const
{
switch (orientation) {
case 0 :
return data[(r << BS) + c];
case 1 :
return data[(c << BS) + (R1 - r)];
case 2 :
return data[((R1 - r) << BS) + (R1 - c)];
case 3 :
return data[((R1 - c) << BS) + r];
default :
return 0 ;
}
}此代碼包括一個簡單的圖像出口商,該出口商將每個臉部呈現到圖像中。
https://www.nayuki.io/page/tiny-png-output
https://github.com/nayuki/nayuki-web-publishered-code
Tiny PNG輸出是一個小型獨立庫,可在C和C ++中使用,它採用RGB8.8.8像素並寫入PNG文件。
可以使用簡單公式估算移動總數。假設多維數據集是足夠隨機的,我們可以期望第一張臉能解決1/6,因此必須移動5/6的零件。第二個面將解決1/5,需要4/5的零件要移動。第三臉3/4,第四張2/3,第五臉1/2,最後一張面部將完全解決。可以在實驗上估計〜2.1的平均移動數(K)。隨著立方體的大小增加,K的值降低。該值永遠不會小於2,因為換向器需要至少2次移動每件。
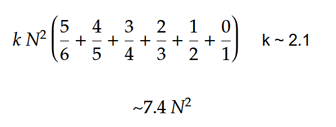
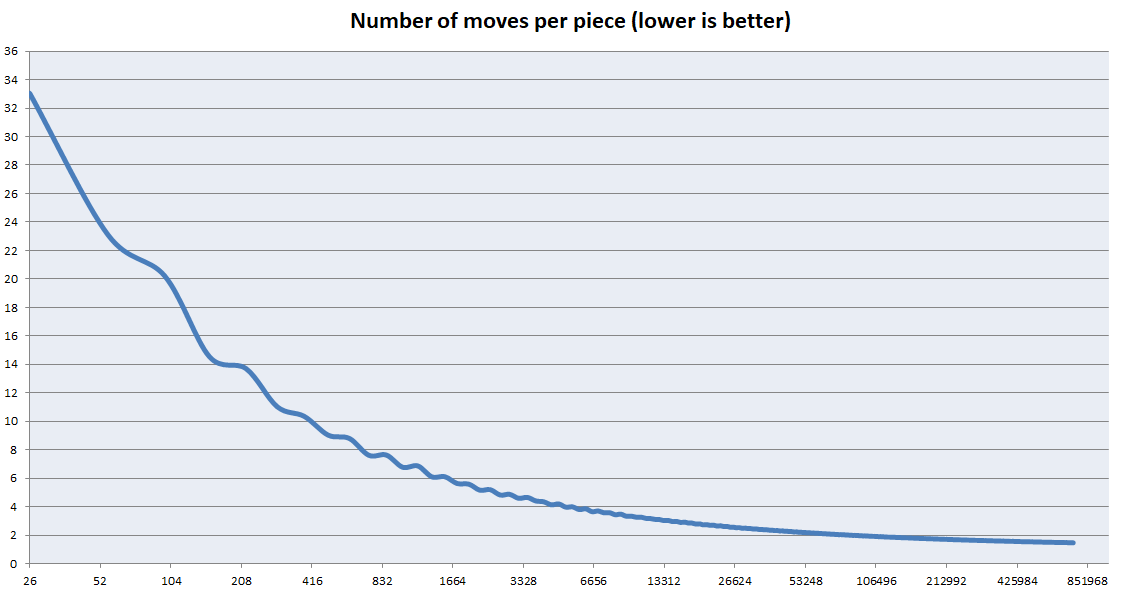
該算法針對非常大的立方體進行了優化。但是,對於小立方體來說是可怕的。主要的優化集中在盡可能快地解決中心,並且沒有考慮解決邊緣。但是,隨著立方體尺寸的增加,與中心相比,邊緣的大小微不足道。下圖顯示瞭如何使用較大的立方體減少每件的平均移動次數。注意:這不是k的圖。它是(總動作) /(零件數)的圖表
cmake -B build -S .
cd build
cmake --build .
RCube/RCube