equivalence testing multiple regression
1.0.0
可以應用等效測試來評估多元回歸模型中單個預測因子的效應是否足夠小，以至於被統計和實際上可忽略不計（Alter＆Counsell，2021）。有關更多信息，請參閱OSF頁面和/或psyarxiv上的免費預印本。
以下功能提供了適當的基於等價的替代方案，以結論多個回歸中預測因子和結果之間可忽略的效果
這些R功能旨在毫不訪問整個數據集，旨在輕鬆適應多個研究環境。這兩個函數reg.equiv.fd()和reg.equiv()提供了相似的輸出，但在用戶所需的輸入信息類型上有所不同。
具體而言，第一個函數reg.equiv.fd()需要R（ lm對象）中的完整數據集和模型，而第二個則不需要。 reg.equiv()旨在針對無法訪問完整數據集但仍希望評估某個預測指標與結果變量的多元回歸中的變量的關聯的研究人員，例如，使用結果部分或結果部分中通常提供的信息表在一篇已發表的文章中報導。
reg.equiv.fd() ：需要完整的數據集datfra=數據框架（例如，mtcars）model=模型，一個LM對象（例如， mod1 ，其中mod1<- mpg~hp+cyl ）delta=最小的效果大小（sesoi），最小有意義的效果大小（MME）或等效間隔的上限（？）（例如，.15）predictor=要測試的預測變量的名稱（例如， "cyl" ）test=測試類型自動設置為兩個單方面測試（Tost; Schuirmann，1987），另一個選擇是Anderson-Hauck（AH； Anderson＆Hauck，1983）std= delta（或，sesoi）是默認情況下標準化的集合。指示性std=FALSE假定不合標準的單元alpha=默認情況下將標稱I類錯誤率設置為.05。要更改，只需指示α級別即可。例如， alpha=.10 reg.equiv.fd()示例：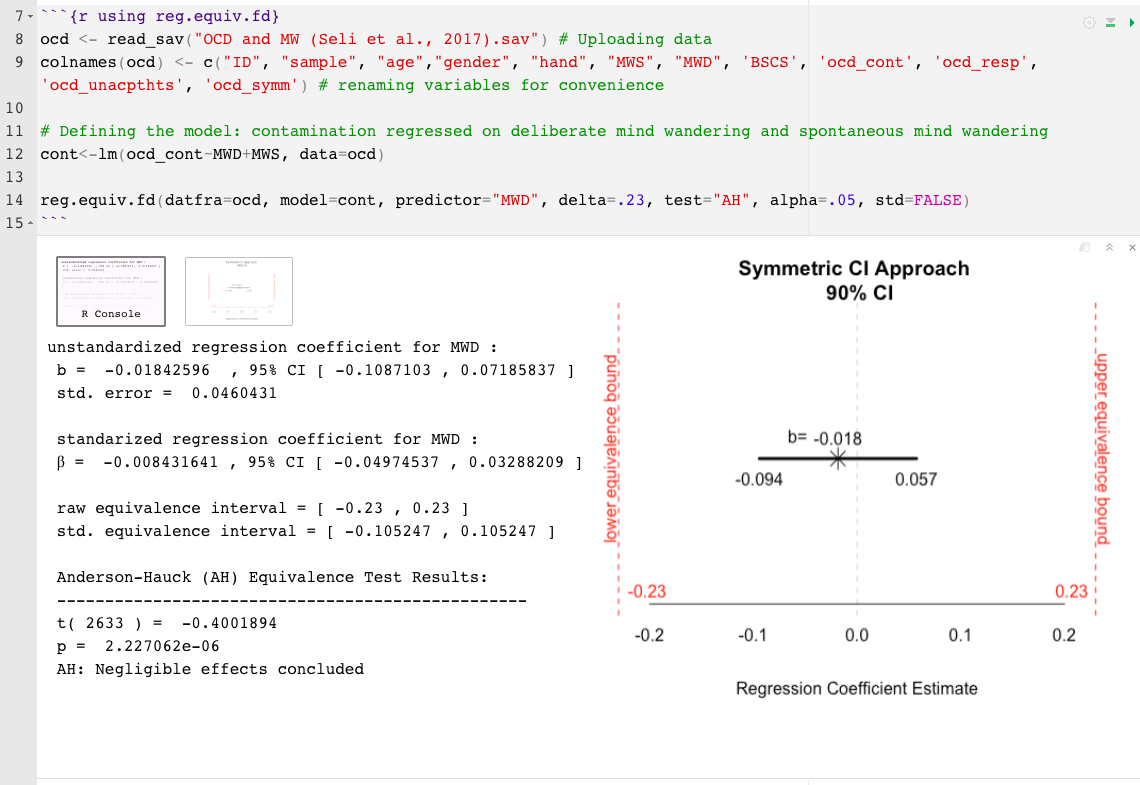 
reg.equiv() ：不需要完整數據集b=與感興趣的預測指標相關的估計效應大小，這可以是標準化的或不可歸的（例如，.02）se=與感興趣的預測因子的效果大小相關的標準誤差（如果效果大小是標準化的，請確保將se值與標準化而不是原始效應相關）p=回歸模型中總預測變量的數量（不包括截距）n=樣本量delta=最小的效果大小（sesoi），最小有意義的效果大小（MME）或等效間隔的上限（？）（例如，.15）predictor=要測試的預測變量的名稱（例如， "cyl" ）test=測試類型自動設置為兩個單方面測試（Tost; Schuirmann，1987），另一個選擇是Anderson-Hauck（AH； Anderson＆Hauck，1983）std= delta（或sesoi）和指示效應大小的設置為默認情況下的標準化。指示性std=FALSE假定不合標準的單元alpha=默認情況下將標稱I類錯誤率設置為.05。要更改，只需指示α級別即可。例如， alpha=.10 reg.equiv()示例：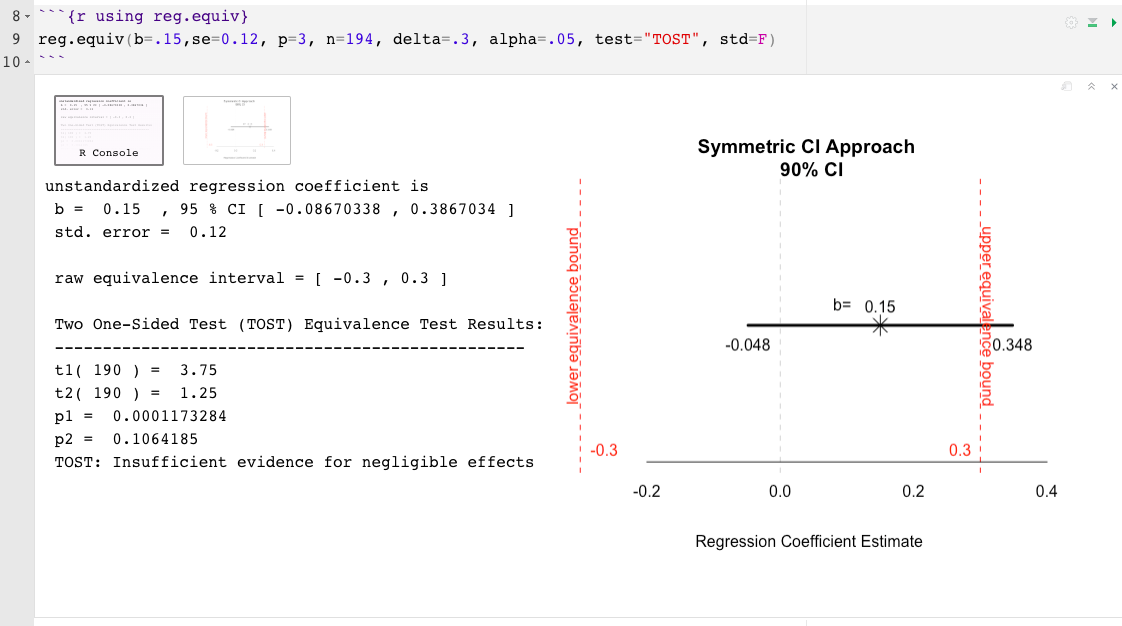 
等效測試是一種在無效的顯著性測試（NHST）框架中設計的方法。 NHST因過度依賴對P值的二分法結果而受到嚴厲批評，或者幾乎沒有考慮效果的大小或其在實踐中的影響（Eg，Cumming，2012; Fidler＆Loftus，2009; Harlow，2009; Harlow，1997; Kirk ，2003; kirk，2003 Lee，2016年）。研究人員必須注意NHST的局限性，並刪除測試結果的實際和統計方面。
為了最大程度地減少p值的局限性，在“可忽略不計”或“證據不足以忽略不計”的結論之外，解釋觀察到的效果的幅度和精度更為信息。觀察到的效果應與等價界限，其不確定性的程度以及其實際含義（或缺乏）有關。因此，此處提供的兩個R函數還包括觀察到效應的圖形表示及其相對於等價間隔的相關不確定性。由此產生的情節有助於說明觀察到的效果及其誤差的近距離或狹窄的程度與等效界限。推斷置信帶與等效間隔的比例和位置可以幫助解釋超過P值的結果。
