autodiff下載 - autodiff源代碼下載

autodiff

其他源碼

1.0.0

下載

Autodiff-自動差異C ++庫

該項目已轉移到增強（數學/差異/自動式），並且該存儲庫不再更新。

建立狀態

分支	特拉維斯	應用程式	codecov.io
`master`
`develop`

描述

AutoDiff是一個僅標題的C ++庫，可促進單個和多個變量的數學函數的自動分化（正向模式）。

該實現是基於在X₀點上的分析函數F的Taylor系列擴展：

Autodiff的基本思想是在評估F（X₀）中用多項式替代數字。通過將數字X替換為一階多項式X₀+ε ，並使用相同的算法來計算F（x₀+ε） ， ε中的結果多項式包含該函數的衍生物f'（x₀） ， f'（x₀）， f''（x₀） ， f'''（x₀） ，...在係數內。每個係數等於其各自秩序的導數，除以該順序的階乘。

更詳細地，假設一個人有興趣計算X f處F的第一個N衍生物。如果不損失計算衍生物的精確度，則可以丟棄包括大於n的功率的所有項O（ ^εn+1 ） 。（這是由於以下事實：多項式中的每個項僅取決於算術操作下的相等和低階項。）在這些截斷規則下， F提供了多項式到多項式轉換：

C ++的超載運算符和功能的能力允許創建代表ε中多項式的類fvar 。因此，在寫入並返回通用（模板）類型的變量時，計算y₀= f（x₀）的數值的相同算法f也用於計算多項式_ʃn y _{n y n} his ε） 。然後從各個階乘n的乘積中找到衍生物F ^（n）（x₀） ！和係數y _n ：

示例1：單變量差異化

計算X到第四功率的導數

 #include <boost/math/difection/autodiff.hpp> #include <iostream> template <typename t>
t fourth_power（t const＆x）{
  t x4 = x * x;  //操作員*（）中的retval通過NRVO使用X4的內存。
  x4 *= x4;      //即使在平方時，也沒有在操作員內製作X4的副本。
  返回x4;     // x4通過nrvo。} int main（）在main（）中使用y的內存{使用名稱空間boost :: math ::差異化;

  constexpr unsigned順序= 5;                  //要計算的最高階導數。
  自動const x = make_fvar <double，order>（2.0）;  //在x = 2處找到衍生物。
  auto const y = fourth_power（x）;  for（無符號i = 0; i <=順序; ++ i）
    std :: cout <<“ y。  返回0;
}/*輸出：y。衍生（0）= 16y。衍生物（1）= 32y.Derivive（2）= 48y.Derivive（3）= 48y.Derivive（4）= 24y。衍生物（5）= 0 */

上述計算

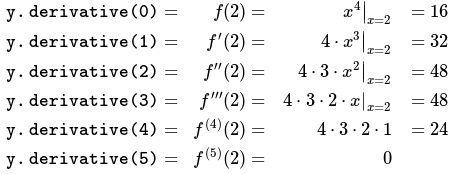
y. derivivic（）呼叫的乳膠

示例2：多變量和多工差異化

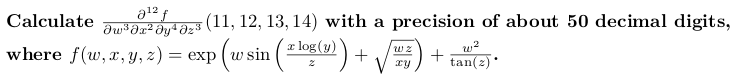
大約50個小數位數的12階混合衍生物

 #include <boost/Math/distriation.hpp> #include <boost/upertRecision/cpp_bin_float.hpp> #include <IoStream>使用namesspace boost :: Mathiation :: Mathiation :: Intelliation; typename z>
促進<w，x，y，z> f（const w＆w，const x＆x，const y＆y，const z＆z）{使用命名空間std;
  返回exp（w * sin（x * log（y） / z） + sqrt（w * z /（x * y））） + w * w / tan（z）;
} int main（）{使用float50 = boost :: multipRecision :: cpp_bin_float_50;  constexpr unsigned nw = 3;  //最大派生級順序以計算W
  constexpr unsigned nx = 2;  //衍生物的最大順序以計算x
  constexpr unsigned ny = 4;  //最大派生階以計算y
  constexpr unsigned nz = 3;  //衍生物的最大順序以計算z
  //將4個自變量一起聲明為std ::元組。
  auto const變量= make_ftuple <float50，nw，nx，ny，nz>（11，12，13，14）;  自動const＆w = std :: get <0>（變量）;  //在W = 11處最多最多NW衍生物
  自動const＆x = std :: get <1>（變量）;  // x = 12時最多可NX衍生物
  自動const＆y = std :: get <2>（變量）;  // y = 13的最多最多紐約導數
  自動const＆z = std :: get <3>（變量）;  //在z = 14時最多可NZ衍生物
  自動const v = f（w，x，y，z）;  //根據Mathematica符號分化計算。
  float50 const答案（“ 1976.31960074777777777779881875290418720908121189218755”）;
  std :: cout << std :: setprecision（std :: numeric_limits <float50> :: digits10）
            <<“ Mathematica：” <<答案<<'n'<<“ autodiff：” << v.derivative（nw，nx，ny，ny，nz）<<'n'n'<< std :: setPrecision（ 3）
            <<“相對錯誤：” <<（V.Derivative（NW，NX，NY，NZ） /答案-1）<<'n';  返回0;
}/*輸出：Mathematica：1976.3196007777777777777777777779818752904187209081211892188AUTODIFF：1976.3196600777777777777777777777777777777777777777777718721121121121121121121121121121121121121121121121121121121121199999999999太體

示例3：黑色 - choles選項的價格自動計算

#include <boost/Math/districiation/autodiff.hpp> #include <Iostream>使用namespace boost :: Math :: Math :: Constants;使用名稱空間BOOST :: MATH :: DINCATION; https://en.wikipedia. org/wiki/greeks_(finance)#formulas_for_european_option_greeks///標準標準累積累積分配函數<typename x>
x phi（x const＆x）{返回0.5 * erfc（-One_div_root_two <x>（） * x）;
}枚舉類CP {呼叫，put}; //假定零年股息收益率（q = 0）.template <typeName價格，TypeName Sigma，typename tau，typename rate>
促銷<Price，Sigma，Tau，Rate> Black_Scholes_option_price（CP CP，Double K，
                                                            價格const＆s，
                                                            Sigma Const＆Sigma，
                                                            tau const＆tau，
                                                            速率const＆r）{使用命名空間std;
  auto const d1 =（log（s / k） +（r + sigma * sigma / 2） * tau） /（sigma * sqrt（tau））;  auto const d2 =（log（s / k） +（r -sigma * sigma / 2） * tau） /（sigma * sqrt（tau））;  switch（cp）{case cp ::呼叫：返回s * phi（d1） -  exp（-r * tau） * k * phi（d2）; case cp :: put：return exp（-r * tau） * k * phi（-d2）-s * phi（-d1）;
  }
} int main（）{double const k = 100.0;                    //罷工價格。
  auto const s = make_fvar <double，2>（105）;  //股票價格。
  雙const sigma = 5;                    //波動。
  雙const tau = 30.0 / 365;             //多年到期的時間。 （30天）。
  double const r = 1.25 / 100;               // 利率。
  auto const call_price = black_scholes_option_price（cp :: call，k，s，s，sigma，tau，r）;  auto const put_price = black_scholes_option_price（cp :: put，k，s，s，sigma，tau，r）;

  std :: cout <<“ black-scholes call price =” << call_price.derivative（0）<<'n'<<“ black-scholes price price =” << put_price.derivative（0）<<'n' <<“ call delta =” << call_price.derivative（1）<<'n'<<“ put delta =” << put_price.derivative（1）<<'n'n'n <<“ call gama =” << call_price 。衍生（2）<<'n'<<“ put gamma =” << put_price.derivative（2）<<'n';  返回0;
}/*輸出：黑色 -  choles呼叫價格= 56.5136Black-scholes put Price = 51.4109CALL delta = 0.773818 put delta = -0.226182CALL gamma = 0.001999852 put Gamma = 0.001999852*/0.00199852*/

有關自動計算的選項希臘人的較大列表，請參見示例/black_scholes.cpp。