smard power forecasting
1.0.0
هذا المستودع مخصص للتنبؤ باستهلاك الطاقة الألماني.
مبنية ومستوحاة من:
مصدر البيانات: سمارد
ضع جميع الملفات التي تم تنزيلها في:
/example/dataset # there is already used dataset included if you pull, but you could update
تحقق من ملف Forecast.Rmd لترى كيف يمكنك تشغيل هذا الرمز على إصدار محدث من SMARD-Data.
المكتبات المستخدمة:
# Probably needed
# Load Packages
# library(fhswf)
# library(tsibbledata)
# library(broom)
# library(readr)
# library(datasets)
# library(timeDate)
# library(qlcal)
# library(corrplot)
# library(mgcv)
# library(MEFM)
# library(TTR)
packages <- c(
"devtools",
"ggplot2",
"dplyr",
"tsibble",
"fable",
"fabletools",
"feasts",
"distributional",
"lubridate",
"tidyr",
"forecast",
"zoo",
"scales",
"fable.prophet"
)
install.packages(packages)
library(devtools)
library(ggplot2)
library(dplyr)
library(tsibble)
library(fable)
library(fabletools)
library(feasts)
library(distributional)
library(lubridate)
library(tidyr)
library(forecast)
library(zoo)
library(scales)
library(fable.prophet)
حاول العمل في المثال/ المجلد للبدء.
# Define datapaths
power_consum_path <- "dataset\stunde_2015_2024\Realisierter_Stromverbrauch_201501010000_202407090000_Stunde.csv"
power_consum_smard_prediction_path <- "dataset\propgnose_vom_smard\Prognostizierter_Stromverbrauch_202401010000_202407090000_Stunde.csv"
# Load Smard Prediction
power_consum_smard_prediction_loaded <- load_power_consum(path=power_consum_smard_prediction_path)
raw_smard_pred <- power_consum_smard_prediction_loaded$raw_data
cleaned_smard_pred <- power_consum_smard_prediction_loaded$cleaned_data
cleaned_smard_pred <- cleaned_smard_pred |>
mutate(.model = "SMARD")
names(cleaned_smard_pred)[names(cleaned_smard_pred) == "PowerConsum"] <- ".mean"
# Load PowerConsum Data
power_consum_loaded <- load_power_consum(path=power_consum_path)
raw_power_consum <- power_consum_loaded$raw_data
cleaned_power_consum <- power_consum_loaded$cleaned_data
# Generate more features
cleaned_power_consum$localName[is.na(cleaned_power_consum$localName)] = "Working-Day"
cleaned_power_consum$MeanLastWeek <- rollapply(cleaned_power_consum$PowerConsum, width = 24*8, FUN = function(x) mean(x[1:(24*8-25)]), align = "right", fill = NA)
cleaned_power_consum$MeanLastTwoDays <- rollapply(cleaned_power_consum$PowerConsum, width = 24*3, FUN = function(x) mean(x[1:(24*3-25)]), align = "right", fill = NA)
cleaned_power_consum$MaxLastOneDay <- rollapply(cleaned_power_consum$PowerConsum, width = 24*2, FUN = function(x) max(x[1:(24*2-25)]), align = "right", fill = NA)
cleaned_power_consum$MinLastOneDay <- rollapply(cleaned_power_consum$PowerConsum, width = 24*2, FUN = function(x) min(x[1:(24*2-25)]), align = "right", fill = NA)
تم إنشاء الميزات التالية من مجموعة البيانات وHoliday API:
| فِهرِس | اسم العمود | وصف |
|---|---|---|
| 1 | تاريخ من | للتحقق من صحة DateIndex (مماثلة، ولكن أولية) |
| 2 | استهلاك الطاقة | استهلاك الطاقة بالميغاواط |
| 3 | DateIndex | الطابع الزمني (yyyy-mm-dd hh:mm:ss) |
| 4 | أيام الأسبوع | Mo، Di، Mi، Do، Fr، Sa، So (أيام الأسبوع باللغة الألمانية) |
| 5 | تاريخ | التاريخ (yyyy-mm-dd) |
| 6 | سنة | سنة yyyy |
| 7 | أسبوع | رقم الأسبوع 0-53 |
| 8 | ساعة | رقم الساعة 0-24 |
| 9 | شهر | رقم الشهر 1-12 |
| 10 | localName | اسم عطلة للطابع الزمني |
| 11 | يوم العمل | 1/0 إذا كان يوم العمل (Werktag) ثم 1 |
| 12 | شهر | 1/0 إذا كان يوم الاثنين 1 |
| 13 | دي | 1/0 إذا كان الثلاثاء 1 |
| 14 | مي | 1/0 إذا كان الأربعاء ثم 1 |
| 15 | يفعل | 1/0 إذا كان الخميس 1 |
| 16 | الأب | 1/0 إذا كان الجمعة ثم 1 |
| 17 | سا | 1/0 إذا كان السبت 1 |
| 18 | لذا | 1/0 إذا كان الأحد ثم 1 (غير مطلوب، إذا تم استخدام الاثنين-السبت) |
| 19 | عطلة | 1/0 إذا كان يوم عطلة ثم 1 |
| 20 | يوم العمل، عطلة نهاية الأسبوع | إذا كان يوم عطلة أو عطلة نهاية الأسبوع أو يوم عمل (بالنسبة لقطع الأراضي، فهو Char.) |
| 21 | عطلة ويوم العمل | 1/0 إذا كانت العطلة في يوم عمل، فإن 1 |
| 22 | LastDayWasNotWorkDay | 1/0 إذا لم يكن اليوم الأخير يوم عمل، فإن 1 |
| 23 | LastDayWasNotWorkDayAndNowWorkDay | 1/0 إذا لم يكن اليوم الأخير يوم عمل وهو الآن يوم عمل، إذن 1 |
| 24 | NextDayIsNotWorkDayAndNowWorkDay | 1/0 إذا لم يكن اليوم التالي يوم عمل وهو الآن يوم عمل، فعندئذٍ 1 |
| 25 | اليوم الأخير كان عطلة وليس عطلة نهاية الأسبوع | 1/0 إذا كان اليوم الأخير عطلة وليس عطلة نهاية الأسبوع فإن 1 |
| 26 | اليوم التالي هو عطلة وليس عطلة نهاية الأسبوع | 1/0 إذا كان اليوم التالي عطلة وليس عطلة نهاية الأسبوع، 1 |
| 27 | اسم العطلة | مشابه لـ localName (اسم العطلة) |
| 28 | نهاية العام | 1/0 إذا كان نهاية العام (الأسبوع 52 أو 53) |
| 29 | الأسبوع الأول من العام | 1/0 إذا كانت بداية العام (الأسبوع الأول) |
| 30 | عطلة ممتدة | 1/0 عطلة متأخرة (6 ساعات في اليوم التالي) |
| 31 | عطلة سلسة | تمديد العطلة + الخطيئة(2*pi(ساعة)+1)/24) |
| 32 | يعنيالأسبوع الماضي | متوسط استهلاك الطاقة للأسبوع الماضي (الإزاحة: 24*8-25) |
| 33 | يعنيLastTwoDays | متوسط استهلاك الطاقة في اليومين الماضيين (التحول: 24*3-25) |
| 34 | MaxLastOneDay | الحد الأقصى لاستهلاك الطاقة في اليوم الأخير (الإزاحة: 24*2-25) |
| 35 | MinLastOneDay | الحد الأدنى لاستهلاك الطاقة في اليوم الأخير (الإزاحة: 24*2-25) |
يوجد في هذه الدراسة مجموعة بيانات لاستهلاك الطاقة في ألمانيا من SMARD للأعوام 2015 - 2024.
يوضح الشكل 1 مجموعة البيانات الأولية ذات القيم المفقودة (الأحمر)، والطوابع الزمنية المكررة (الأحمر الداكن)، واستهلاك الطاقة بمرور الوقت (الرمادي)، والدقة لكل ساعة. مع وجود قيمة واحدة مفقودة وتكرار واحد كل عام، كان من السهل تنظيف مجموعة البيانات. عموما مجموعة نظيفة تقريبا. بعد تنظيف مجموعة البيانات، هناك ملاحظات معقولة لاستهلاك الطاقة:
هناك طريقة بسيطة لملء الفجوات من خلال أخذ الملاحظة الأخيرة (ممكن، لأن الدقة كبيرة بما يكفي ولأن هناك عددًا قليلاً فقط من القيم المفقودة). تم الاحتفاظ بالقيمة الأولى للتكرارات.
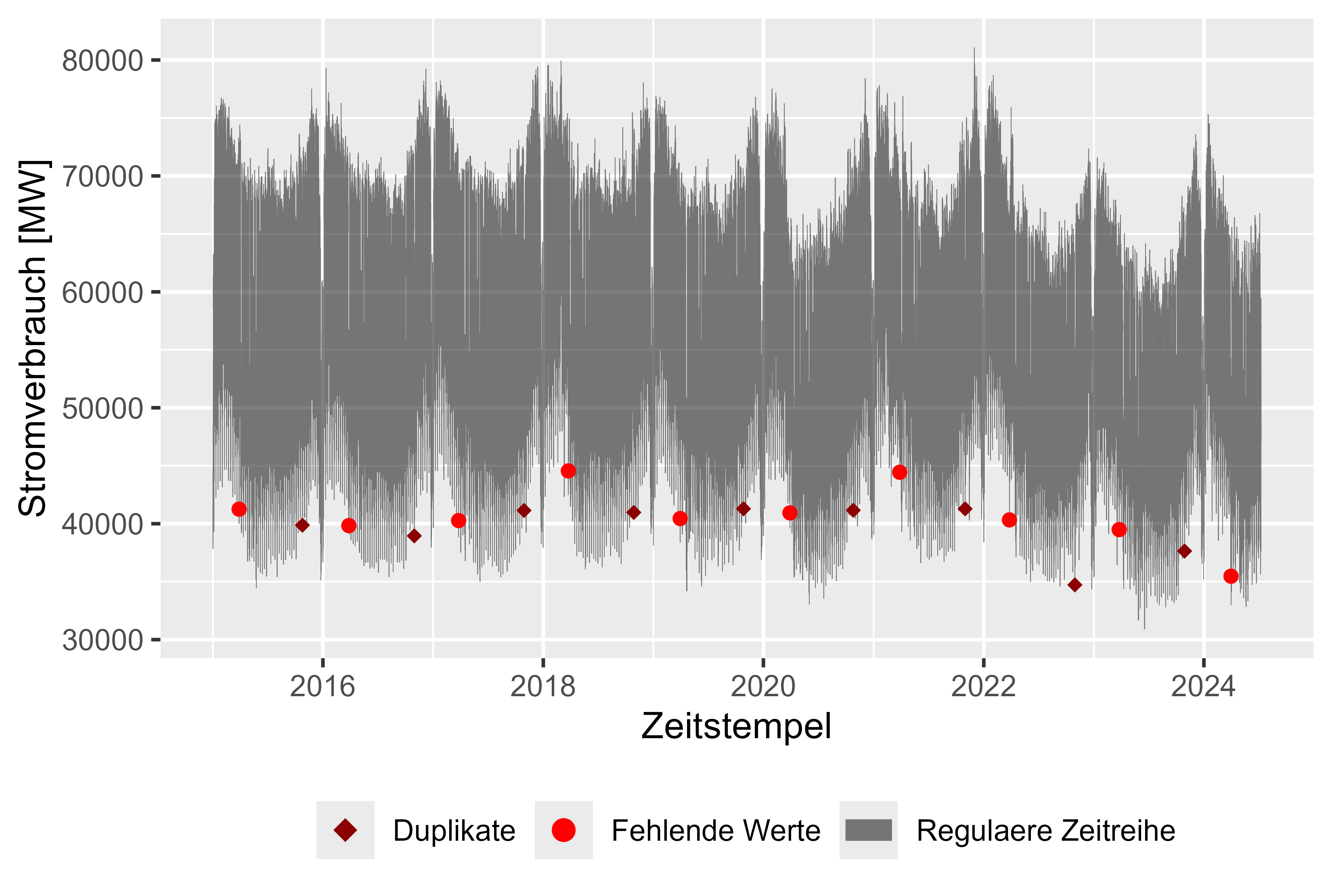الشكل 1: استهلاك الطاقة الخام
local_name_colors <- c(
"Christi Himmelfahrt" = palette()[2],
"Erster Weihnachtstag" = palette()[2],
"Karfreitag" = palette()[2],
"Neujahr" = palette()[2],
"Ostermontag" = palette()[2],
"Pfingstmontag" = palette()[2],
"Reformationstag" = palette()[2],
"Tag der Arbeit" = palette()[2],
"Tag der Deutschen Einheit" = palette()[2],
"Zweiter Weihnachtstag" = palette()[2],
"Regulärer Tag" = palette()[1]
)
week_colors <- c(
"Mo" = palette()[1],
"Di" = palette()[1],
"Mi" = palette()[1],
"Do" = palette()[1],
"Fr" = palette()[1],
"Sa" = palette()[2],
"So" = palette()[2]
)
working_colors <- c("1" = "#2E9FDF", "0" = "#FC4E07")
whw_colors <- c(
"FeiertagnKein Wochenende" = "black",
"Kein FeiertagnKein Wochenende" = "red",
"Kein FeiertagnWochenende" = "orange",
"FeiertagnWochenende" = "blue"
)
p <- cleaned_power_consum |>
gg_tsdisplay(PowerConsum, plot_type = "partial", lag = 100)
ggsave(
"plots/power_consum_acf_pacf.png",
plot = p,
width = 5.5,
height = 3.7,
dpi = 600
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MinLastOneDay.png",
x = "MinLastOneDay",
y = "PowerConsum",
x_label = "Minimaler Stromverbrauch vom letzten Tag [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MaxLastOneDay.png",
x = "MaxLastOneDay",
y = "PowerConsum",
x_label = "Maximaler Stromverbrauch vom letzten Tag [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MeanLastWeek.png",
x = "MeanLastWeek",
y = "PowerConsum",
x_label = "Durchschnittlicher Stromverbrauch der letzten 7 Tage [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MeanLastTwoDays.png",
x = "MeanLastTwoDays",
y = "PowerConsum",
x_label = "Durchschnittlicher Stromverbrauch der letzten 2 Tage [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "WorkdayHolidayWeekend",
file_name = "plots\workday_holiday_weekend_histogram.png",
colors = whw_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Wochenende oder Feiertage",
name_1 = "Werktag"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "WorkDay",
file_name = "plots\workday_histogram.png",
colors = working_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Wochenende oder Feiertage",
name_1 = "Werktag"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "Holiday",
file_name = "plots\holiday_histogram.png",
colors = working_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Werktag oder Wochenende",
name_1 = "Feiertag"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "HolidayAndWorkDay",
file_name = "plots\holiday_workday_histogram.png",
colors = working_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Wochenende oder Werktag",
name_1 = "Feiertag am Werktag"
)
plot_by_group(
cleaned_power_consum,
group_name = "HolidayName",
file_name = "plots\holiday_boxplot.png",
colors = local_name_colors,
title = "Übersicht der einzelnen Feiertage",
y="PowerConsum",
y_label="Stromverbrauch [MW]",
x_label="Jahre"
)
plot_by_group(
cleaned_power_consum,
group_name = "Weekday",
file_name = "plots\weekday_boxplot.png",
colors = week_colors,
title = "Übersicht der einzelnen Wochentage",
y = "PowerConsum",
y_label="Stromverbrauch [MW]",
x_label="Jahre"
)
plot_by_group(
cleaned_power_consum,
group_name = "WorkDay",
file_name = "plots\workday_boxplot.png",
colors = working_colors,
title = "Übersicht, ob Feiertag (FALSE) oder Werktag (TRUE)",
y = "PowerConsum",
y_label="Stromverbrauch [MW]",
x_label="Jahre"
)
plot_by_column(
df = cleaned_power_consum,
x = "Hour",
y = "PowerConsum",
x_label = "Stunden",
y_label = "Stromverbrauch [MW]",
file_name = "plots\hour_boxplot.png",
title = "Übersicht der einzelnen Stunden"
)
plot_by_column(
df = cleaned_power_consum,
x = "Month",
y = "PowerConsum",
x_label = "Monate",
y_label = "Stromverbrauch [MW]",
file_name = "plots\month_boxplot.png",
title = "Übersicht der einzelnen Monate"
)
plot_by_column(
df = cleaned_power_consum,
x = "Week",
y = "PowerConsum",
x_label = "Woche",
y_label = "Stromverbrauch [MW]",
file_name = "plots\week_boxplot.png",
title = "Übersicht der einzelnen Wochen"
)
plot_by_column(
df = cleaned_power_consum,
x = "Year",
y = "PowerConsum",
x_label = "Jahr",
y_label = "Stromverbrauch [MW]",
file_name = "plots\year_boxplot.png",
title = "Übersicht der einzelnen Jahre"
)
plot_year_month_week_day(
df=cleaned_power_consum,
date_column="DateIndex",
y="PowerConsum",
from_year=2015,
to_year=2024,
from_week=0,
to_week=53,
year_for_week=2018,
from_day=1,
to_day=30,
month_for_day=4,
year_for_day=2018,
from_month=1,
to_month=12,
year_for_month=2018,
holiday="Holiday",
day_of_week = "Weekday"
)
سوف تتناول الأقسام التالية المزيد والمزيد من التفاصيل حول البيانات. سنبدأ هنا بالتمثيل السنوي.
الشكل 2 يمثل التمثيل السنوي للأعوام 2015-2024. ونلاحظ هنا أنه في بداية العام هناك زيادة في استهلاك الطاقة وفي نهاية العام هناك انخفاض (عيد الميلاد، رأس السنة). بشكل عام يبدو مثل شكل الابتسامة أو القوس.
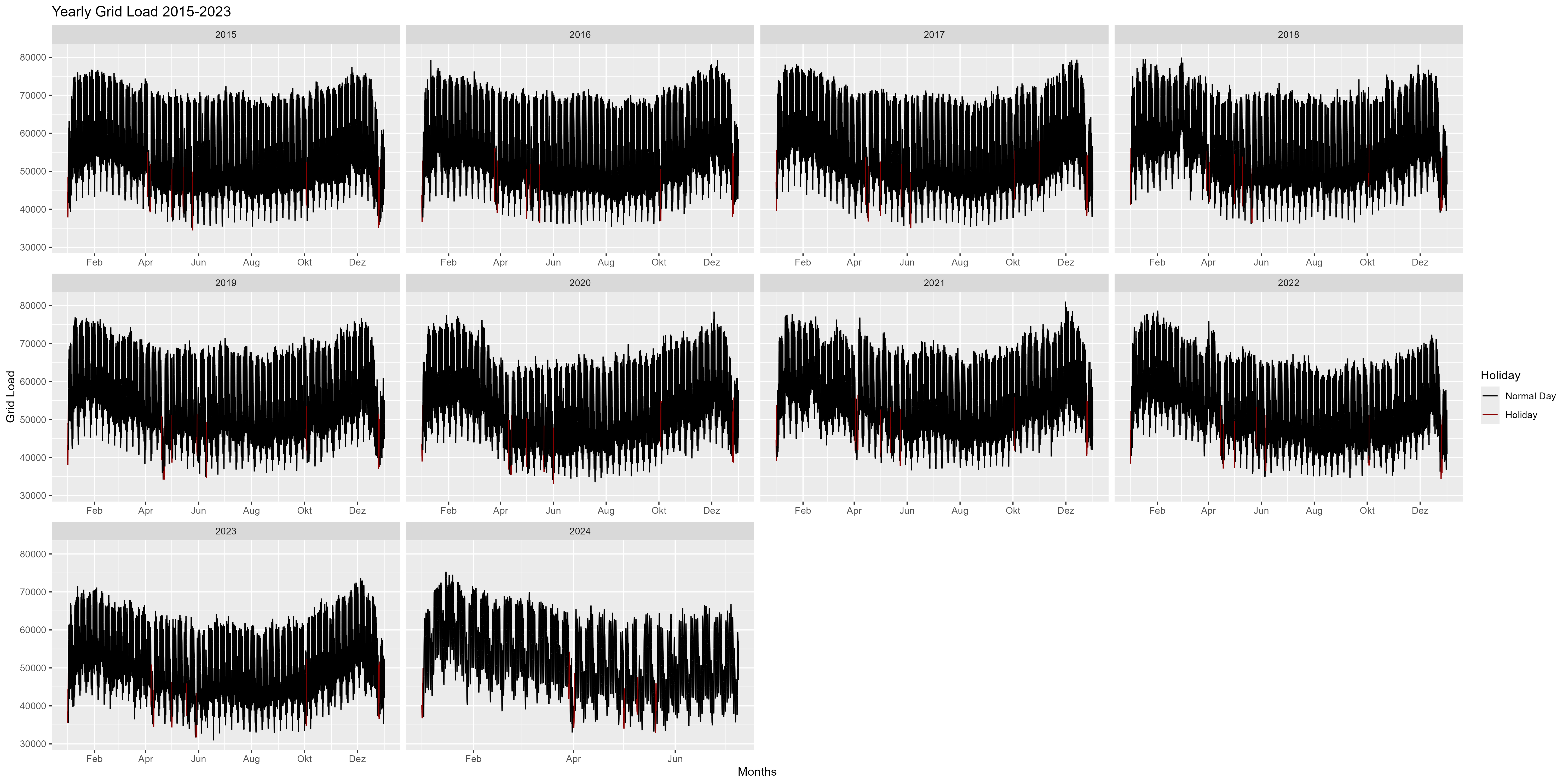الشكل 2: استهلاك الطاقة كل عام كوجه واحد
دعونا نحاول تجميع كل السنوات وتقسيمها إلى أسابيع. تجمع المخططات الصندوقية في الشكل 3 بين جميع السنوات. يمكننا أن نرى النمط بمزيد من التفاصيل. يتم تمثيل بداية ونهاية العام باللون الأحمر ويظهر انخفاضًا عن "شكل الابتسامة" العادي.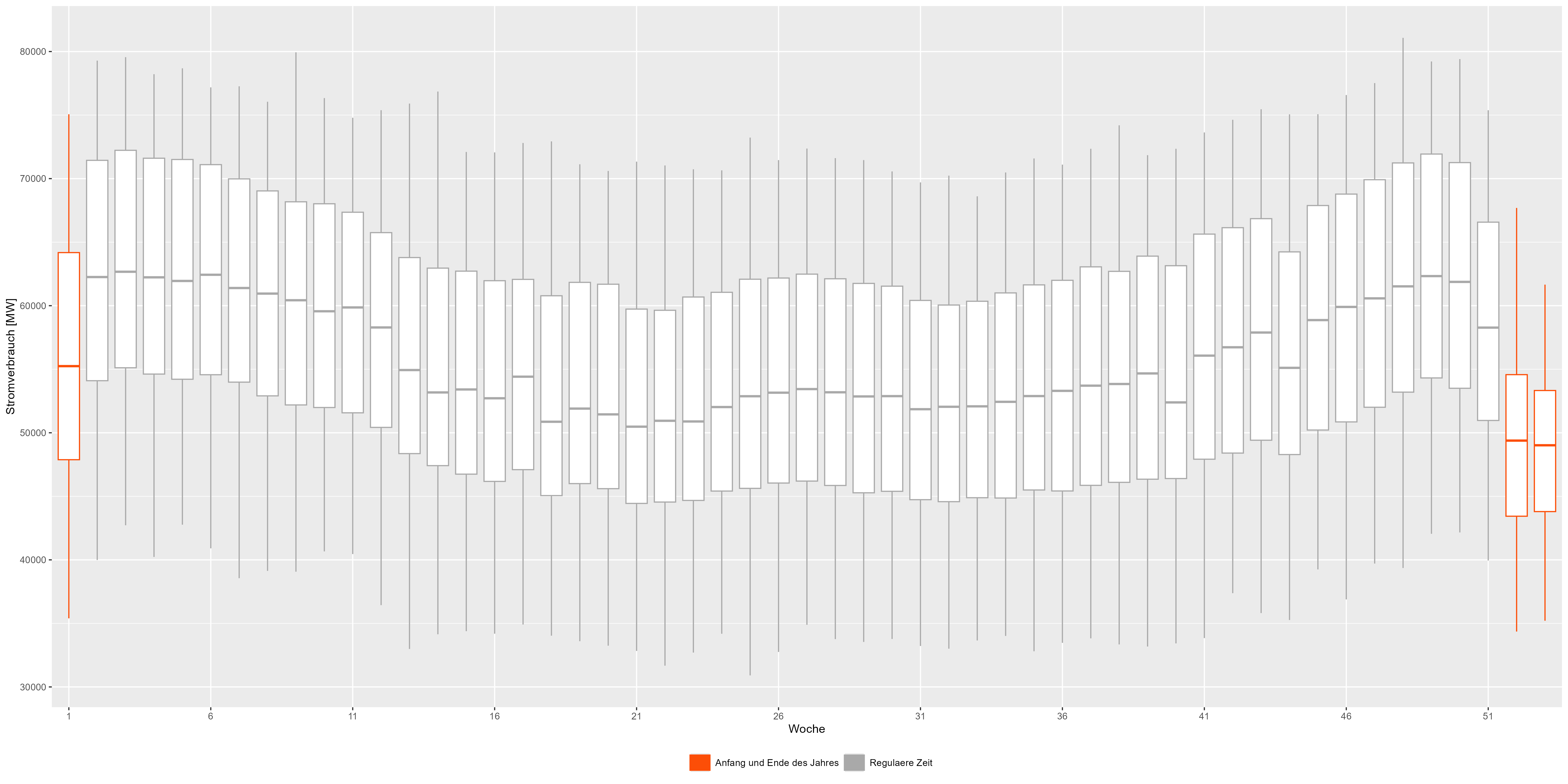
الشكل 3: البيانات المجمعة الأسبوعية لاستهلاك الطاقة
دعونا نذهب بمزيد من التفاصيل وننظر إلى عام 2018 على سبيل المثال. الشكل 4 هو التمثيل الشهري لعام 2018. وهنا يمكننا أن نلاحظ بمزيد من التفصيل نهاية العام. في حوالي 24 ديسمبر، هناك انخفاض في استهلاك الطاقة. ومن الجدير بالذكر أيضًا هنا عطلات نهاية الأسبوع والأعياد (الحمراء). انخفاض لجميع عطلات نهاية الأسبوع ولجميع العطلات.
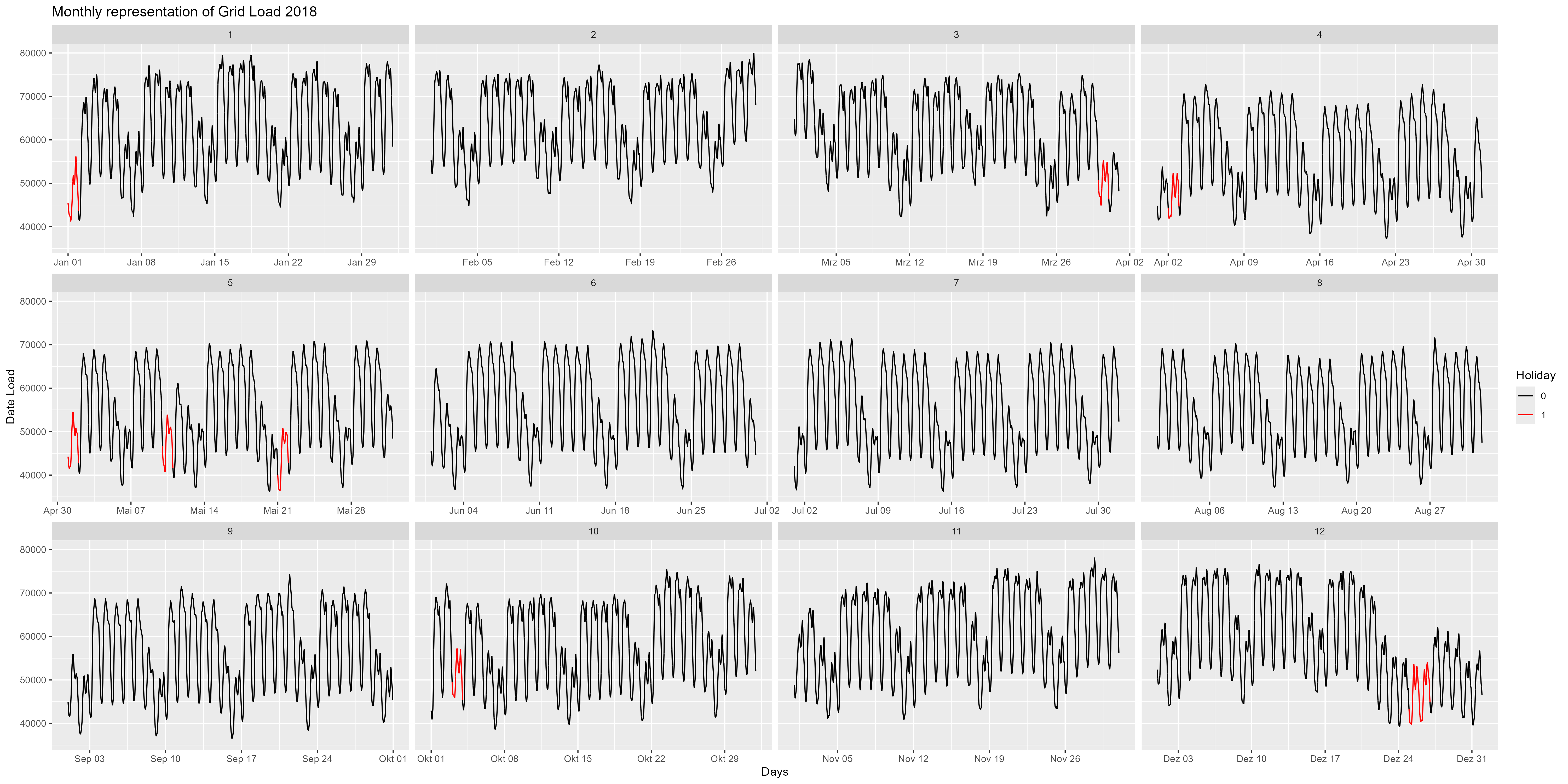الشكل 4: استهلاك الطاقة كل شهر كوجه واحد
يمكننا أن نذهب إلى أبعد من ذلك ونتحقق من تمثيل البيانات على مدار الساعة. ويبين الشكل 5 مخطط boxplot المجمع لكل ساعة. هناك أيضًا انخفاض في ساعات الليل (21:00-06:00) وزيادة في ساعات النهار / وقت العمل (06:00-21:00). أيضًا نمط يجب تضمينه في النموذج.
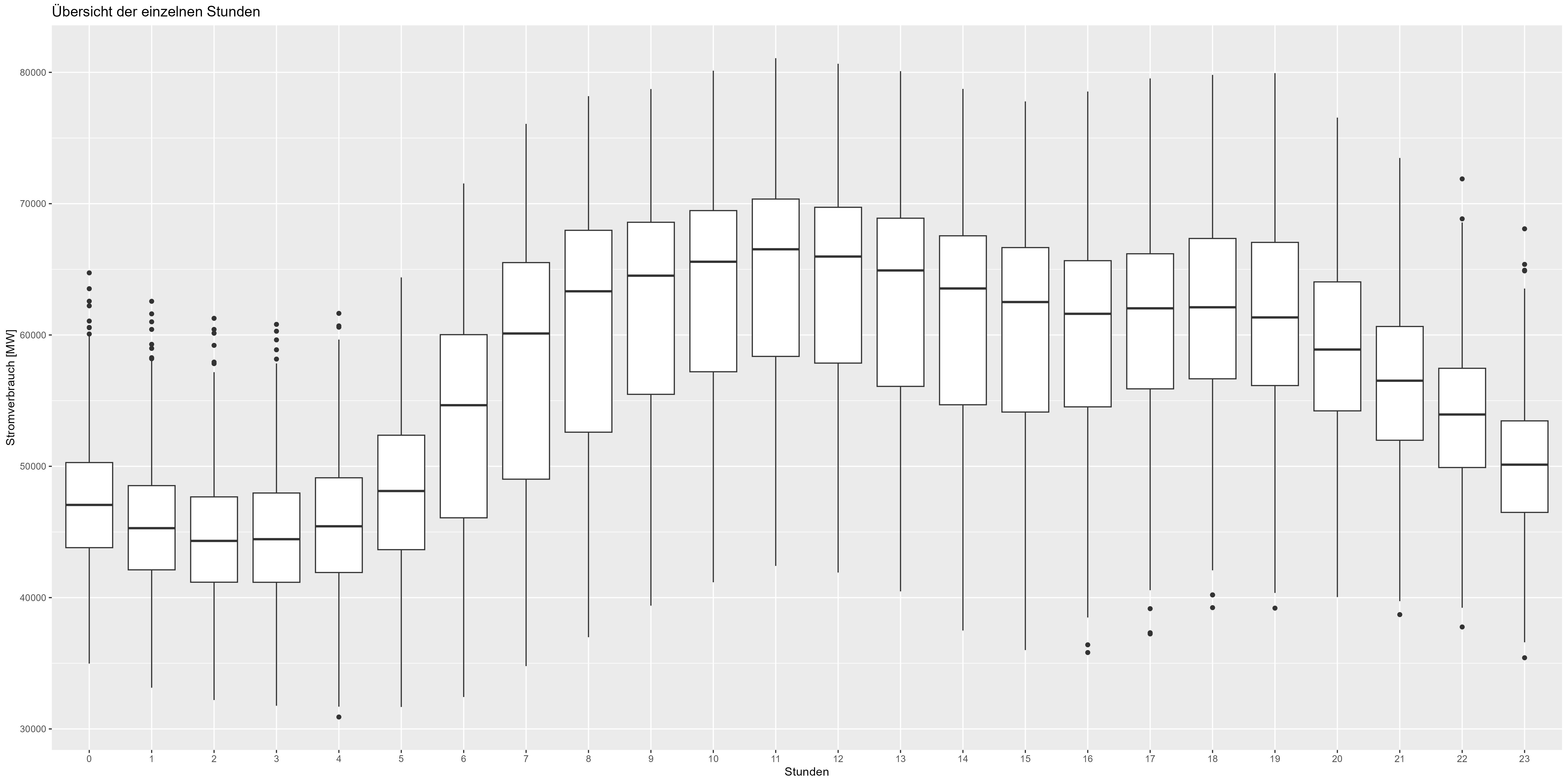الشكل 5: البيانات المجمعة لاستهلاك الطاقة كل ساعة
دعونا نتحدث عن أيام الأسبوع. كما هو مفترض في عطلة نهاية الأسبوع، ينخفض استهلاك الطاقة. "Durchschnitt" هو المتوسط. ويبين الشكل 6 جميع أيام الأسبوع (مجمعة) على مر السنين. هناك انخفاض قدره ~ 10.000 ميجاوات في عطلات نهاية الأسبوع.
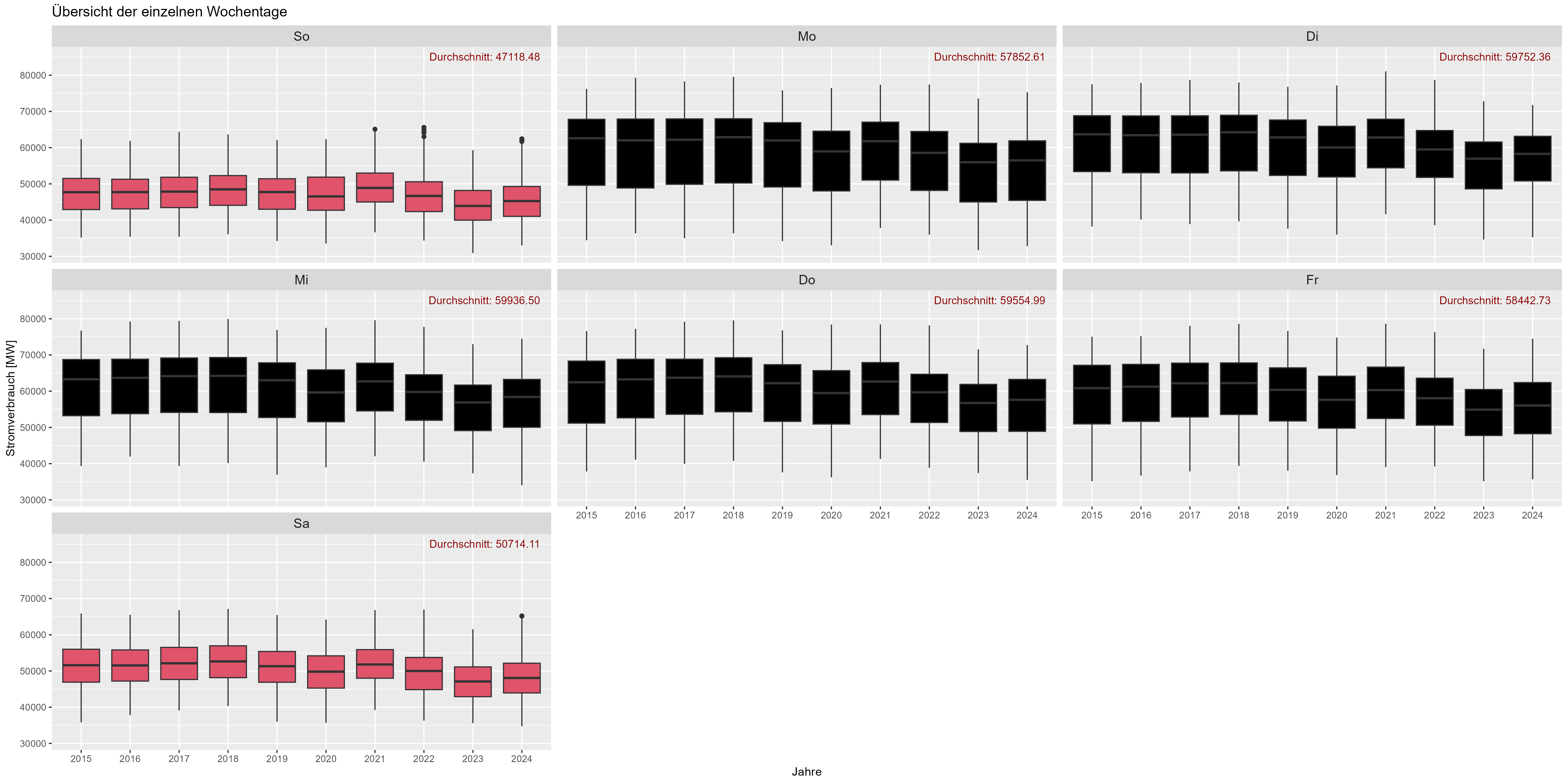الشكل 6 استهلاك الطاقة "تأثير يوم من الأسبوع"
ويبين الشكل 8 تأثير العطلة. "Durchschnitt" هو متوسط استهلاك الطاقة على مر السنين. هناك زيادة كبيرة في استهلاك الطاقة في "أيام العمل" (الرمادي الداكن) مقارنة بأيام العطل (الأحمر). يمكننا أن نفترض هنا أن العطلات تعمل مثل عطلات نهاية الأسبوع بالنسبة لاستهلاك الطاقة".
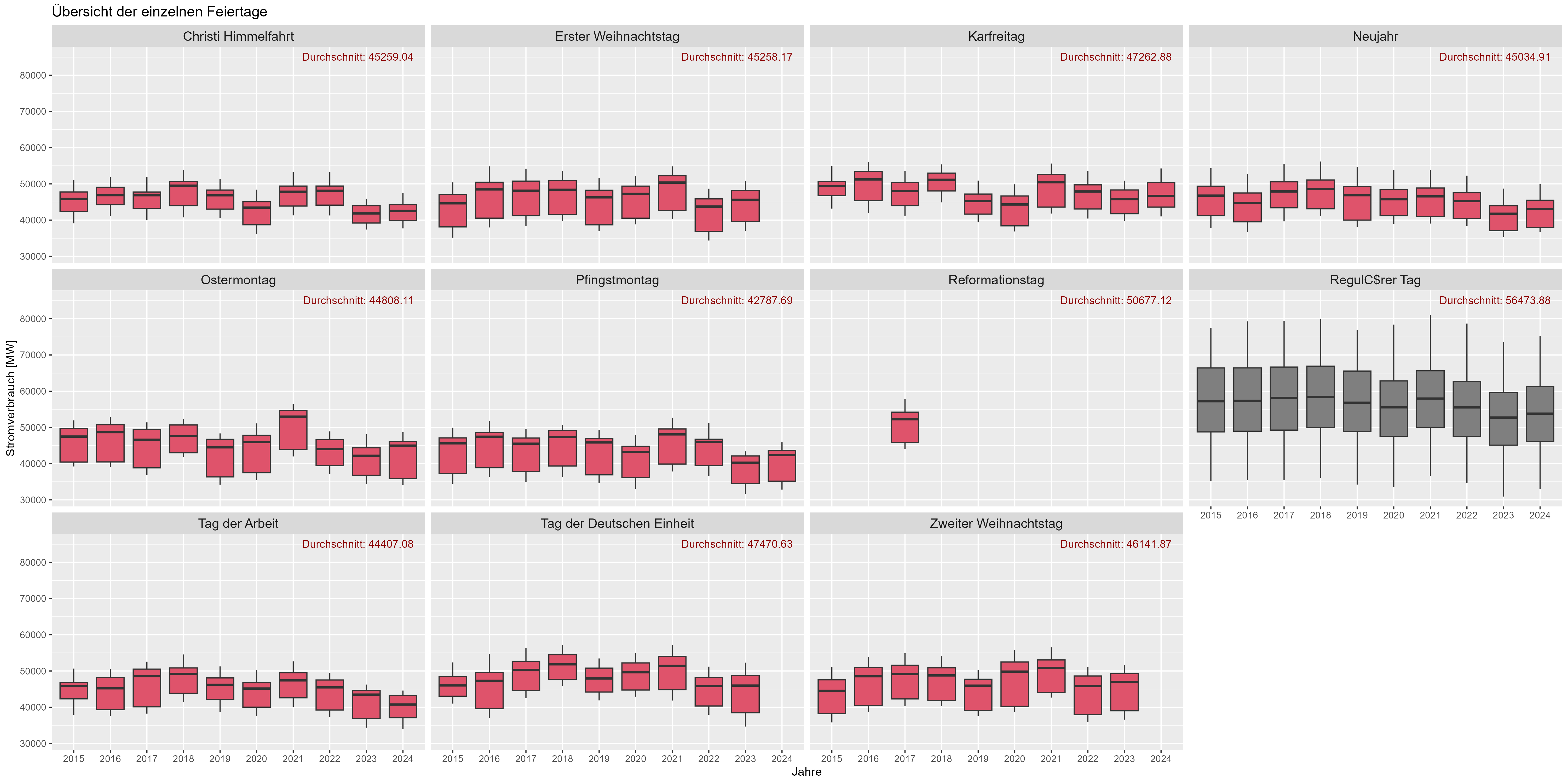الشكل 6 استهلاك الطاقة "تأثير العطلة"
يمثل الشكل 7 سلوكيات مختلفة لأيام مختلفة. هناك 4 فئات. "Feiertag Kein Wochenende" تعني أنها عطلة، ولكنها ليست عطلة نهاية الأسبوع. "Feiertag Wochenende" تعني أنها عطلة وعطلة نهاية الأسبوع. "Kein Feiertag Kein Wochenende" تعني أنه يوم عمل عادي و"Kein Feiertag Wochenende" تعني أنه مجرد عطلة نهاية الأسبوع. ويمكن أن نلاحظ توزيعات مماثلة لأيام العمل غير المنتظمة كما هو مفترض.
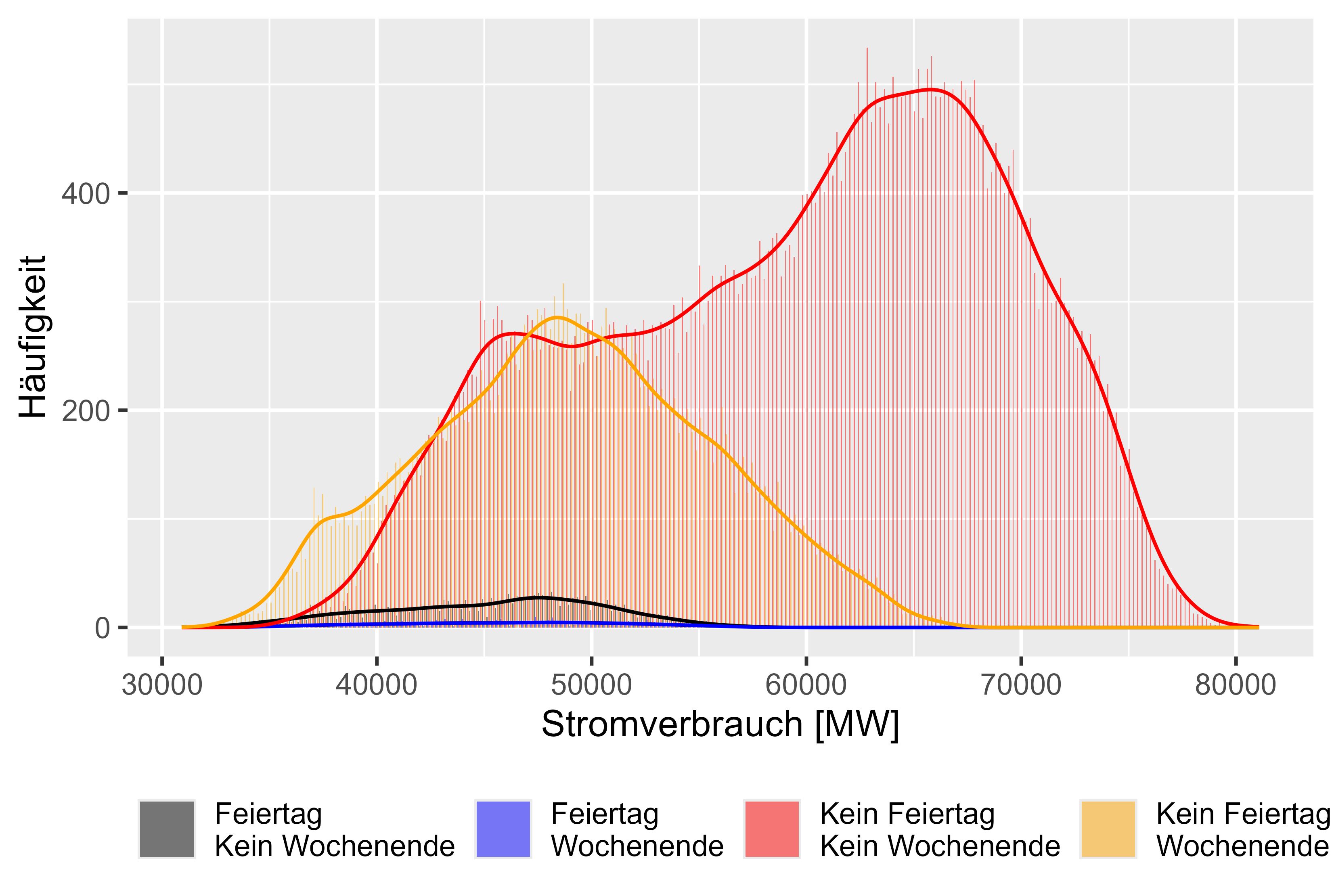الشكل 7: مقارنة استهلاك الطاقة "التأثيرات المختلفة".
يتم إنشاء ميزات متأخرة مثل MeanLastTwoDays وMeanLastWeek وMaxLastOneDay وMinLastOneDay.
مشابه كما تمت مناقشته في DOI: 10.1109/TPWRS.2011.2162082 - التنبؤ بالأحمال على المدى القصير بناءً على نموذج مضاف شبه بارامتري
تمثل الأشكال 8-11 (اللون الأحمر ليس أيام العمل) هذه القيم المتأخرة مقابل استهلاك الطاقة الفعلي.
هناك ارتباط خفيف لهذه الميزات المولدة.
# Check Correlation
cor <- cor(cleaned_power_consum[sapply(cleaned_power_consum, is.numeric)], method = c("pearson", "kendall", "spearman"), use = "complete.obs")
| ميزة | العلاقة مع PowerConsum |
|---|---|
| عطلة سلسة | -0.556194 |
| يعنيالأسبوع الماضي | 0.389044 |
| يعنيLastTwoDays | 0.201253 |
| MaxLastOneDay | 0.320193 |
| MinLastOneDay | 0.348583 |
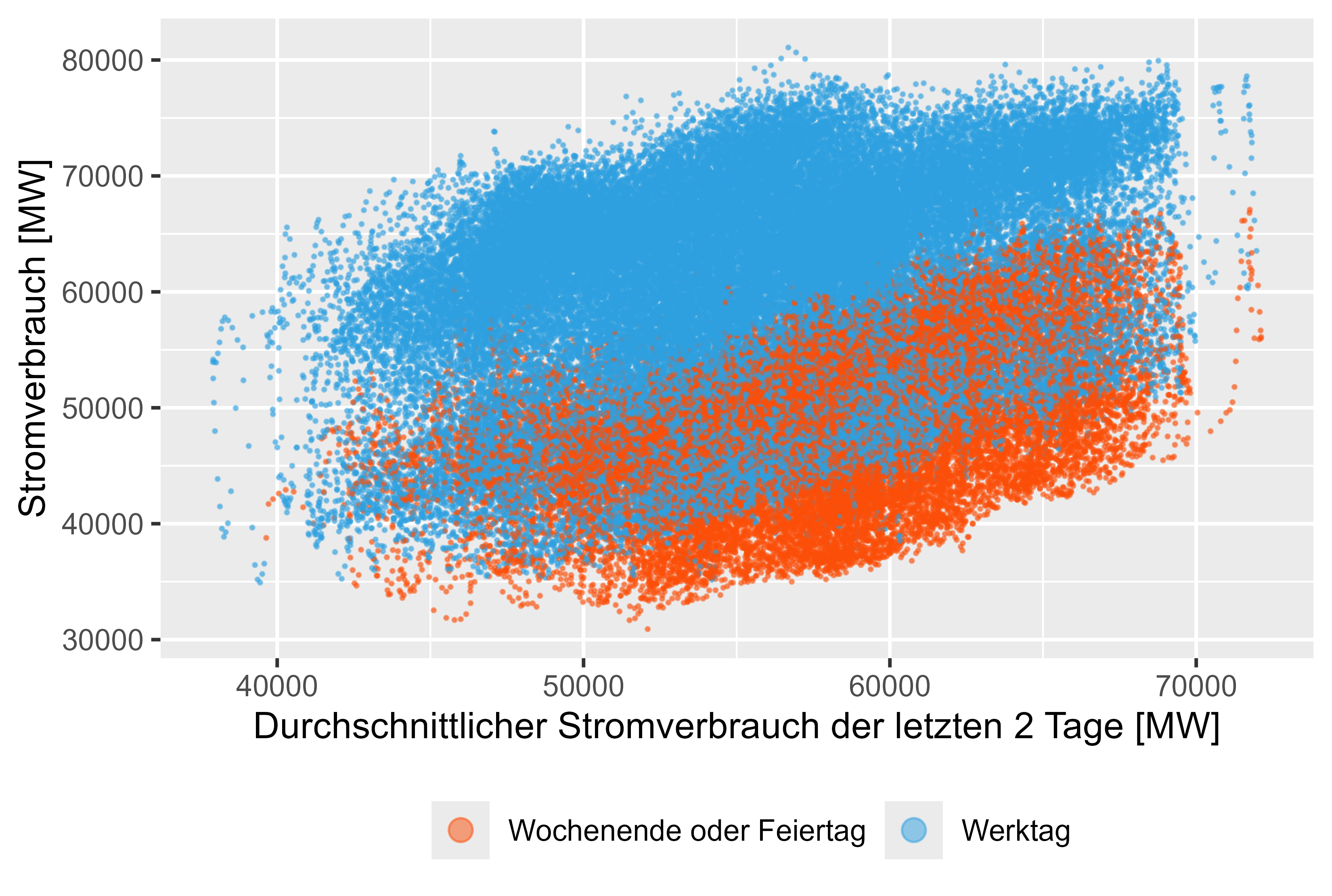الشكل 8: استهلاك الطاقة - متوسط آخر يومين
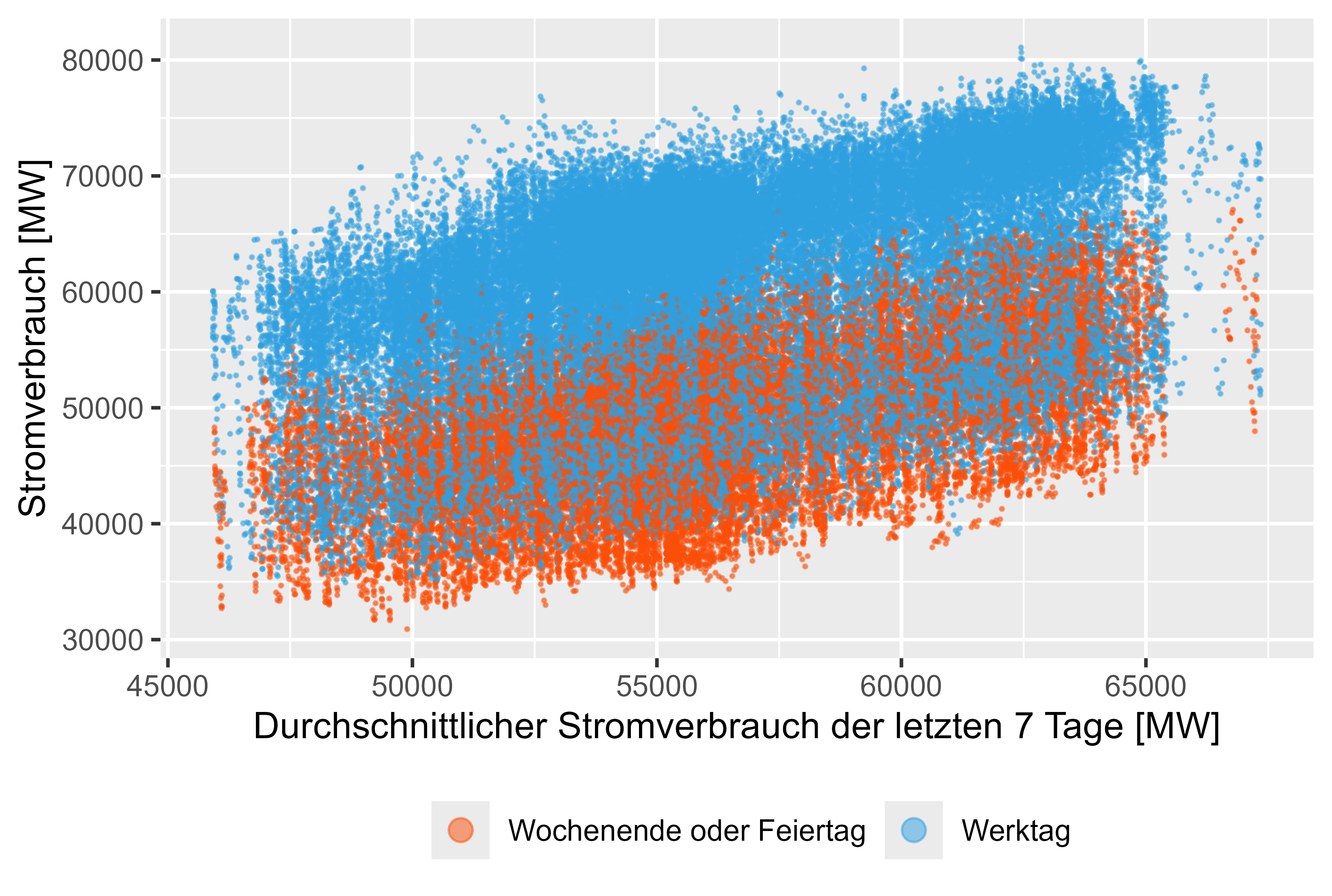الشكل 9: استهلاك الطاقة - متوسط الأسبوع الماضي
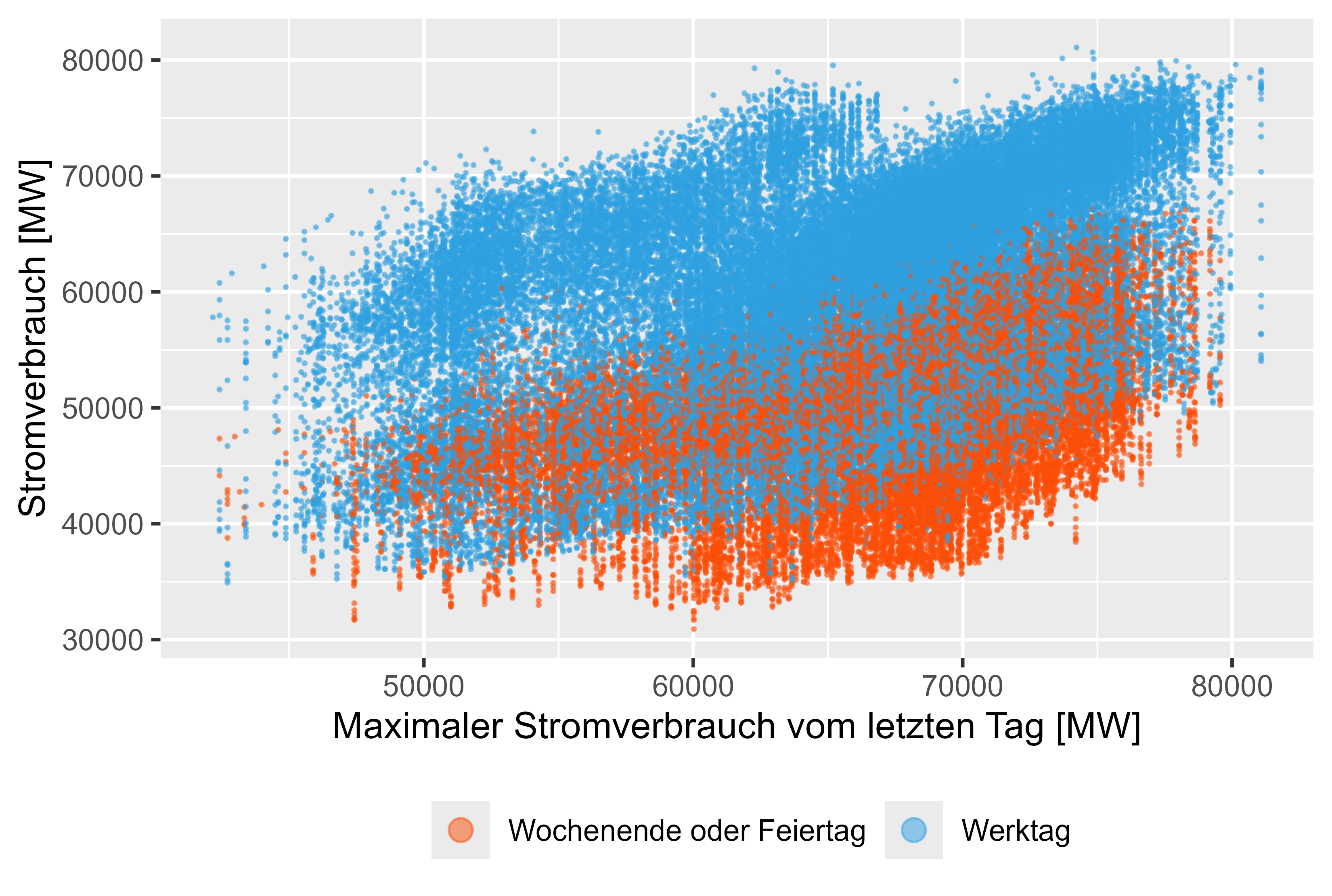الشكل 10: استهلاك الطاقة - MaxLastOneDay
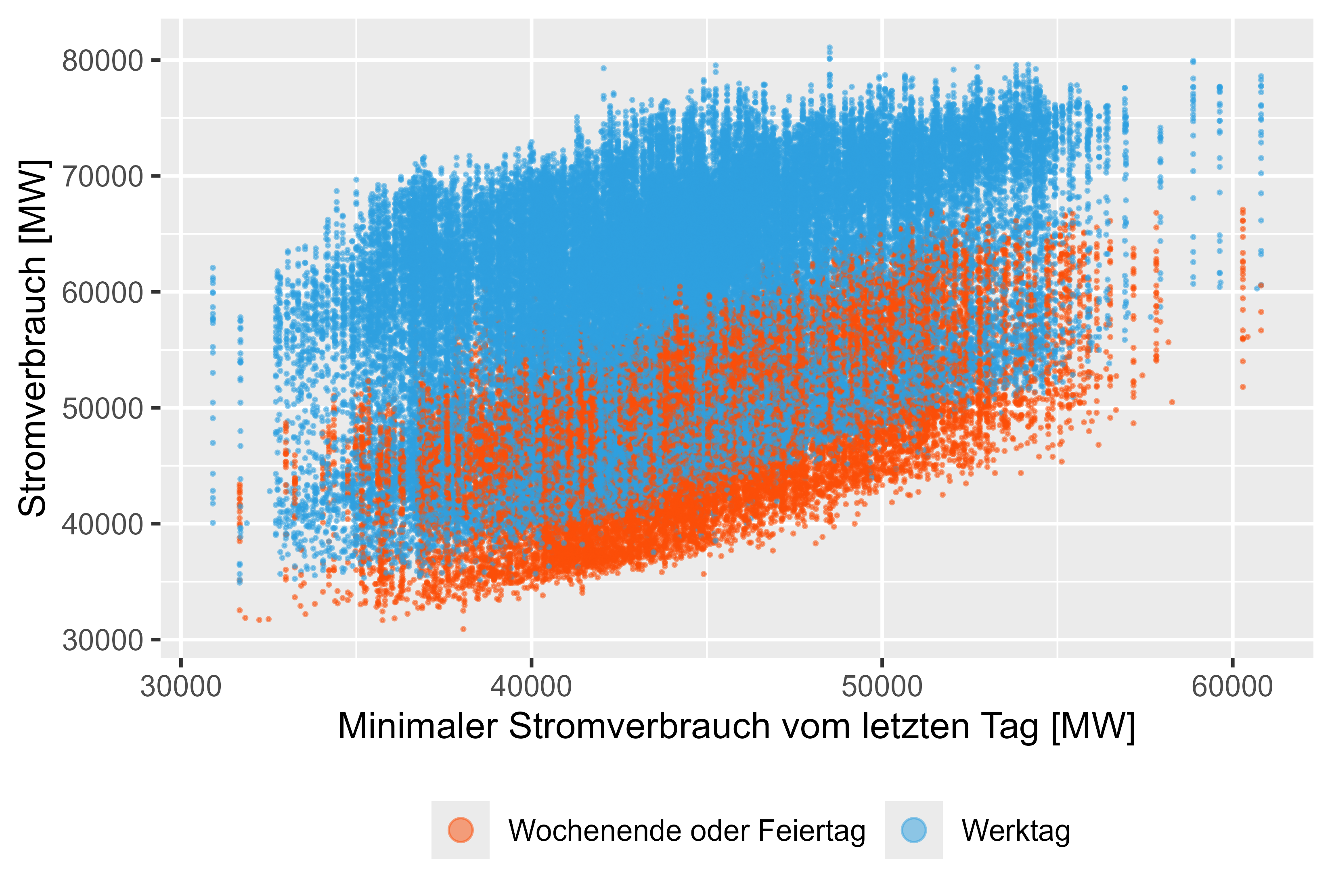الشكل 11: استهلاك الطاقة - MinLastOneDay
هناك موسمية معقدة. بالنسبة للدقة بالساعة، هناك موسمية سنوية وأسبوعية ويومية. وهو ما يحتاج إلى تتبعه بواسطة النموذج. الحل هنا كما تمت مناقشته في التنبؤ: المبادئ والممارسة الفصل 12.1 الموسمية المعقدة لاستخدام مصطلحات فورييه لتمثيل وتجميع عبر cos() وsin() الموسمية المعقدة.
يمكننا إلقاء نظرة بسيطة على مخططي ACF وPACF، حيث يوجد عدد قليل من الارتفاعات المهمة، ولكنه مجرد تمثيل لـ 96 قيمة متأخرة. إذا أخذنا ~ 9000 ملاحظة متأخرة لمدة عام، فسيكون هناك موسمية معقدة. ولهذا السبب فمن الأسهل استخدام مصطلح فورييه. كما أنها لم تعمل بشكل جيد بمجرد العثور على مكونات PDQ و pdq
ARIMA(...
stepwise=FALSE,
greedy=FALSE,
approx=FALSE)
نفسها. كما يزيد وقت التدريب بشكل كبير بدون شروط فورييه.
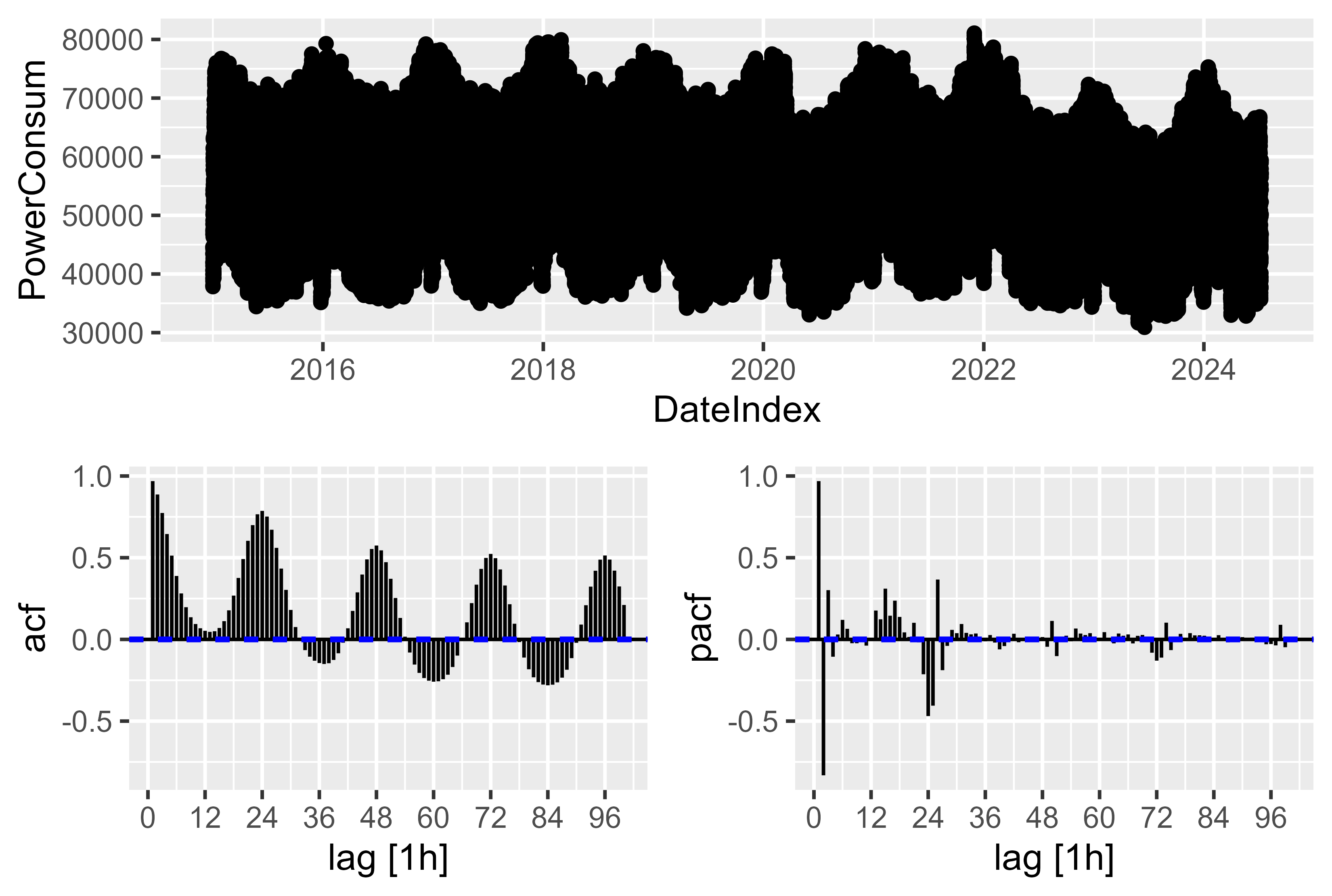الشكل 12: استهلاك الطاقة - مخطط ACF PACF لاستهلاك الطاقة الخام
أفضل مجموعة ميزات موجودة في هذا العمل هي:
لمقارنة النماذج نستخدم المقاييس MAE وMAPE. SMARD هو نموذج "Bundesnetzagentur" من صفحة SMARD. لقد تم أيضًا تجربة النموذج النبوي، وكان أداؤه قويًا، ولكنه ليس جيدًا بما فيه الكفاية.
وصلت القيم المتوقعة لـ SMARD إلى MAPE بنسبة 3.6%. <- ليس في هذه الدراسة.
بيانات التدريب:
أفضل نموذج تم العثور عليه حتى الآن في الحرب LHM + DHR (النموذج التوافقي الخطي + الانحدار التوافقي الديناميكي)
والفكرة هي تجميع نموذج خطي مع نموذج ARIMA. لأنه كان من الصعب على نموذج ARIMA التعامل مع المتغيرات الوهمية للعطلات. لذلك ساعد النموذج المجمع.
train_power_consum <- cleaned_power_consum |>
filter(year(DateIndex) > 2020 & (year(DateIndex) < 2024))
generate_models(model_name = "model/mean_naive_drift",
train_power_consum = train_power_consum)
train_power_consum_v5 <- train_power_consum |>
mutate(HolidaySmoothed = Holiday + sin(2 * pi * (as.numeric(Hour)+1) / 24))
holiday_effect_model <- lm(
PowerConsum ~
HolidaySmoothed,
data = train_power_consum_v5
)
saveRDS(holiday_effect_model, file = "ensemble_model/version_5/holiday_effect_2021_2023.rds")
train_power_consum_v5$Residuals <- residuals(holiday_effect_model)
fit <- train_power_consum_v5 |>
model(
ARIMA = ARIMA(Residuals ~
PDQ(0,0,0)
+ pdq(d=0)
+ MeanLastWeek
+ WorkDay
+ EndOfTheYear # new
+ FirstWeekOfTheYear # new
+ MeanLastTwoDays
+ MaxLastOneDay
+ MinLastOneDay
+ fourier(period = "day", K = 6)
+ fourier(period = "week", K = 7)
+ fourier(period = "year", K = 3)
)
)
saveRDS(fit, file = "ensemble_model/version_5/arima_2021_2023.rds")
يمكننا تصور التأثير وكيفية عمل النموذج. ويبين الشكل 13 الفكرة وراء هذا النموذج. بادئ ذي بدء، نلائم نموذج LHM ونحسب البقايا. تدريب نموذج DHR من المخلفات وتلخيص كليهما. إنها مرآة نوعًا ما على LHM وتدفع القيم إلى الأعلى.
بالنسبة لنموذج LHM، نستخدم هنا نهجًا بسيطًا وهو منحنى الجيوب الأنفية الذي يتكرر كل 24 ساعة ويقل أو يزيد في أيام العطلات أو أيام العمل.
من خلال التنبؤ بـ LHM على البيانات الجديدة، يمكننا التنبؤ ببقايا البيانات الجديدة. المخلفات + LHM تعيد القيم إلى الموضع "الصحيح".
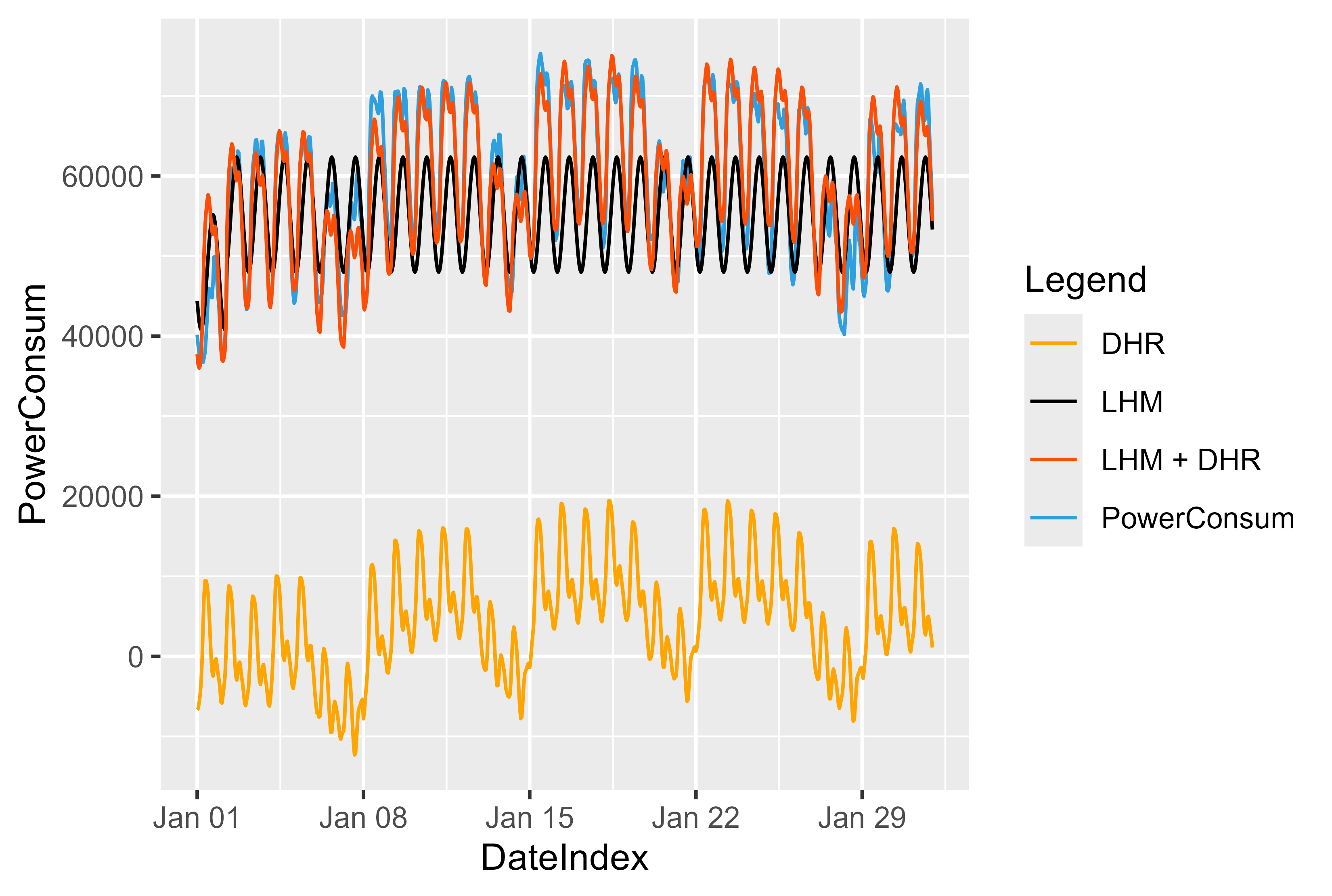الشكل 13: تمثيل نموذج LHM + DHR
ensembled_fc <- load_ensembled_models(
days_to_forecast = 40,
months_to_forecast = 6,
year_to_forecast = 2024,
starting_month = 1,
real_data = cleaned_power_consum,
smard_fc = cleaned_smard_pred,
model_path = "ensemble_model"
)
all_forecasts_ensembled <- ensembled_fc$all_forecasts
raw_fc_ensembled <- ensembled_fc$raw_forecasts
fc <- load_all_model_results(
days_to_forecast = 40,
months_to_forecast = 6,
year_to_forecast = 2024,
starting_month = 1,
smard_fc = cleaned_smard_pred,
real_data = cleaned_power_consum
)
all_forecasts <- fc$combined_forecasts
raw_fc <- fc$raw_forecasts
metric_results <- calculate_metrics(fc_data = all_forecasts, fc_data_ensembled=all_forecasts_ensembled)
# Plot best Model for single Models
name_of_best_model_for_single_model <- plot_forecast(
all_forecasts = all_forecasts,
metric_results = metric_results,
cleaned_power_consum = cleaned_power_consum,
raw_fc = raw_fc,
month_to_plot = 1,
days_to_plot = 40
)
# Plot best Model for ensembled Models
name_of_best_model_ensembled <- plot_forecast_ensembled(
all_forecasts = all_forecasts_ensembled,
metric_results = metric_results,
cleaned_power_consum = cleaned_power_consum,
month_to_plot = 1,
days_to_plot = 40
)
# Residuals Compared with SMARD
plot_compare_with_smard(
all_forecasts = all_forecasts_ensembled,
name_of_best_model = name_of_best_model_ensembled
)
# LHM DHM representation
plot_representation_of_lhm_dhm_components(path_dhm = "ensemble_model/version_5/arima_2021_2023.rds",
path_lhm = "ensemble_model/version_5/holiday_effect_2021_2023.rds",
from_month = 1,
to_month = 1,
raw_fc_ensembled = raw_fc_ensembled)
درجة قوية من MAPE 3.8% للإصدار_5 (نموذج LHM + DHR).
دعونا نلقي نظرة أعمق إذا كنا سنستخدم فقط نموذج ARIMA (arima_14). ويمثل الشكل 14 نتائج هذا النموذج. يمكننا أن نرى العطلات (البرتقالية)، وعطلة نهاية الأسبوع (الحمراء)، واليوم العادي (الأزرق). هناك قيم متطرفة كبيرة للعطلات، على الرغم من وجود متغير وهمي لنموذج ARIMA، إلا أنه لم يتمكن من التقاط العطلات بشكل صحيح.
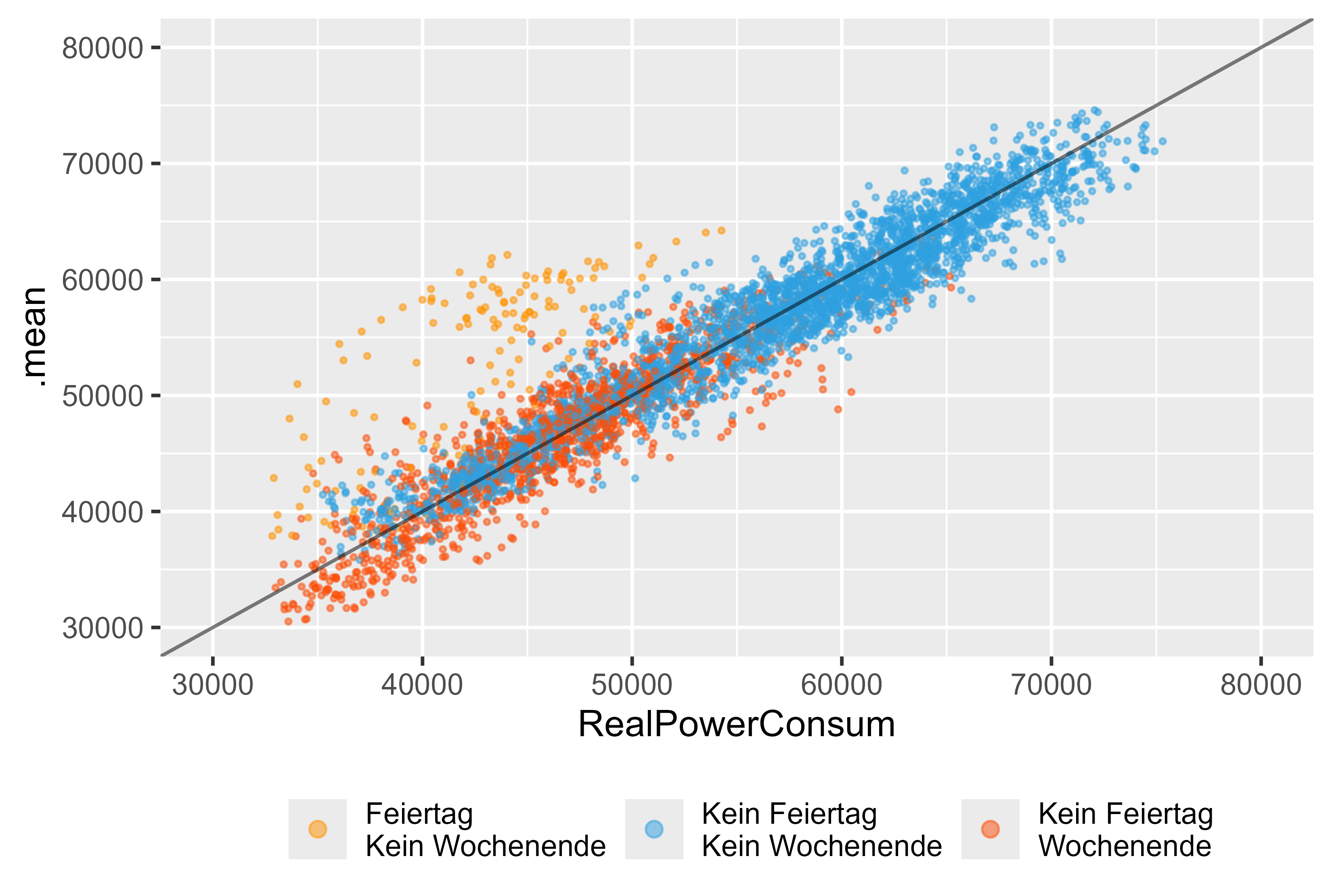الشكل 14: التوقعات مقابل القيم الفعلية ARIMA (DHR, arima_14)، كنموذج واحد
من ناحية أخرى يظهر نموذج LHM + DHR أداء أفضل في أيام العطل. ويمثلها الشكل 15.
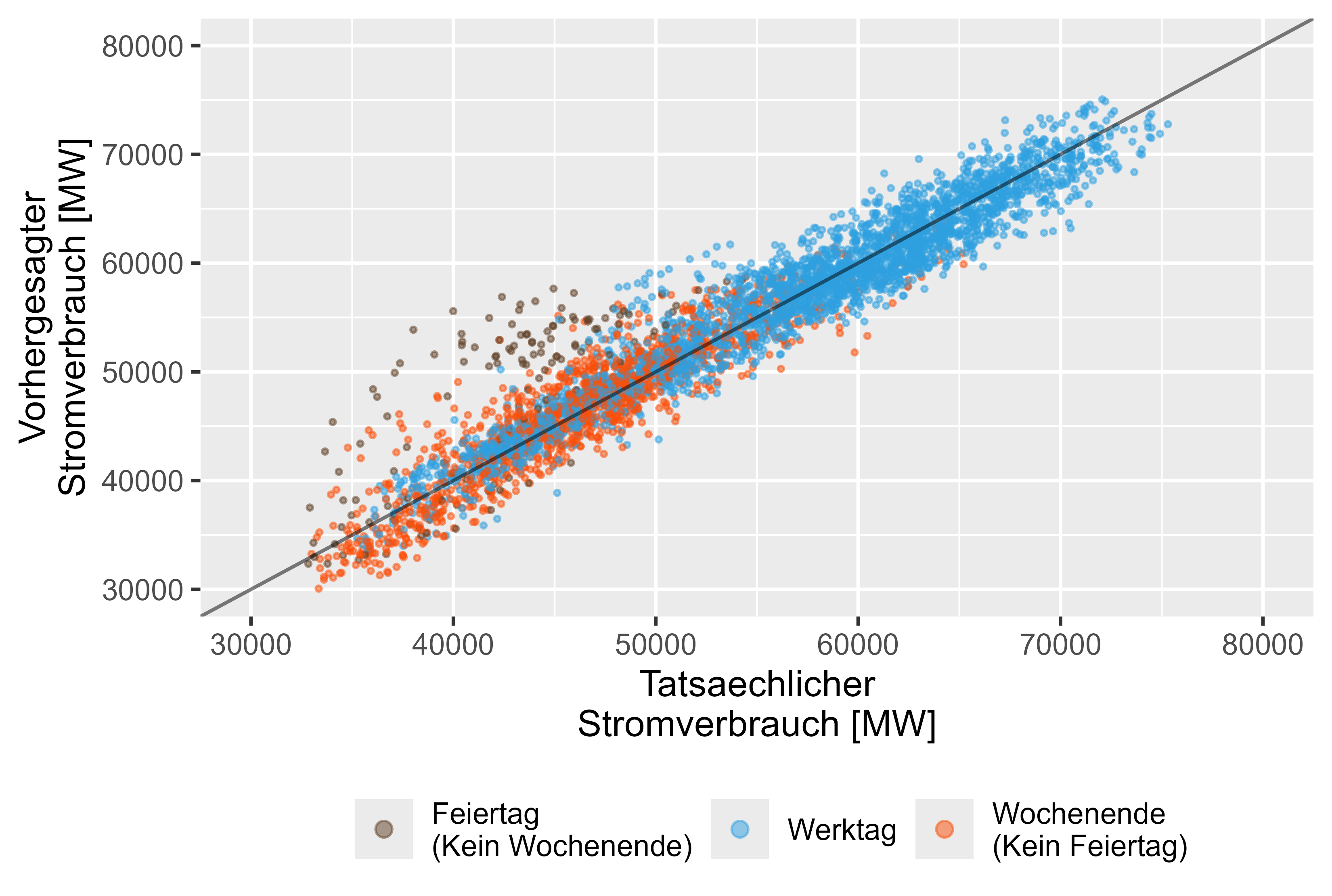الشكل 15: التوقعات مقابل القيم الفعلية LHM + DHR، النموذج المجمع
يوضح الشكل 16 التوقعات لشهر يناير 2024. وهي تبدو معقولة.
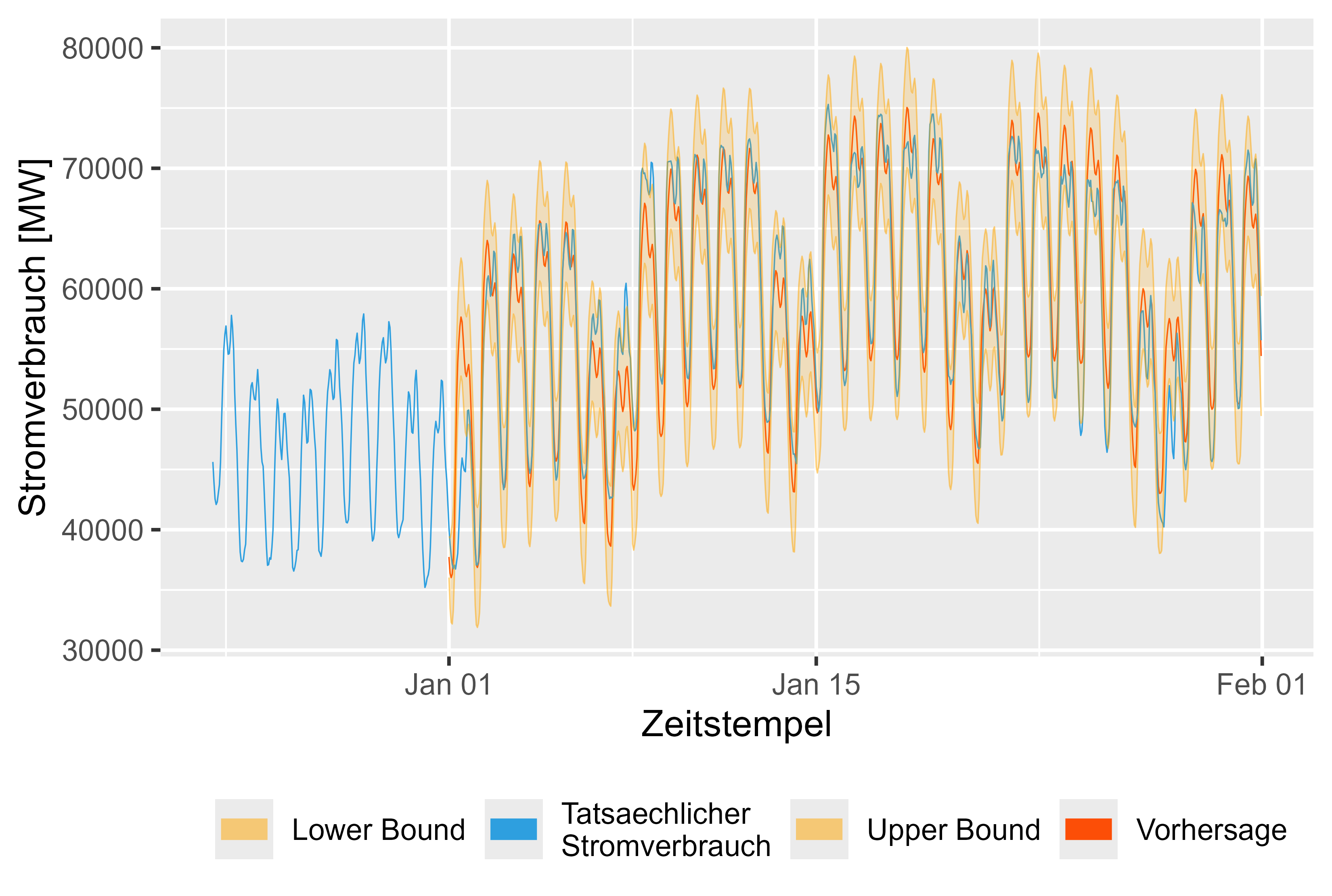الشكل 16 التوقعات مقابل القيم الفعلية LHM + DHR لشهر يناير 2024
كما أن بقايا النموذج مقارنةً بنموذج SMARD تبدو جيدة. هناك عدد قليل من الارتفاعات التي يمكن أن تكون كبيرة ويمكن إعدادها بشكل أفضل من خلال النمذجة. لكن في المجمل نتيجة قوية.
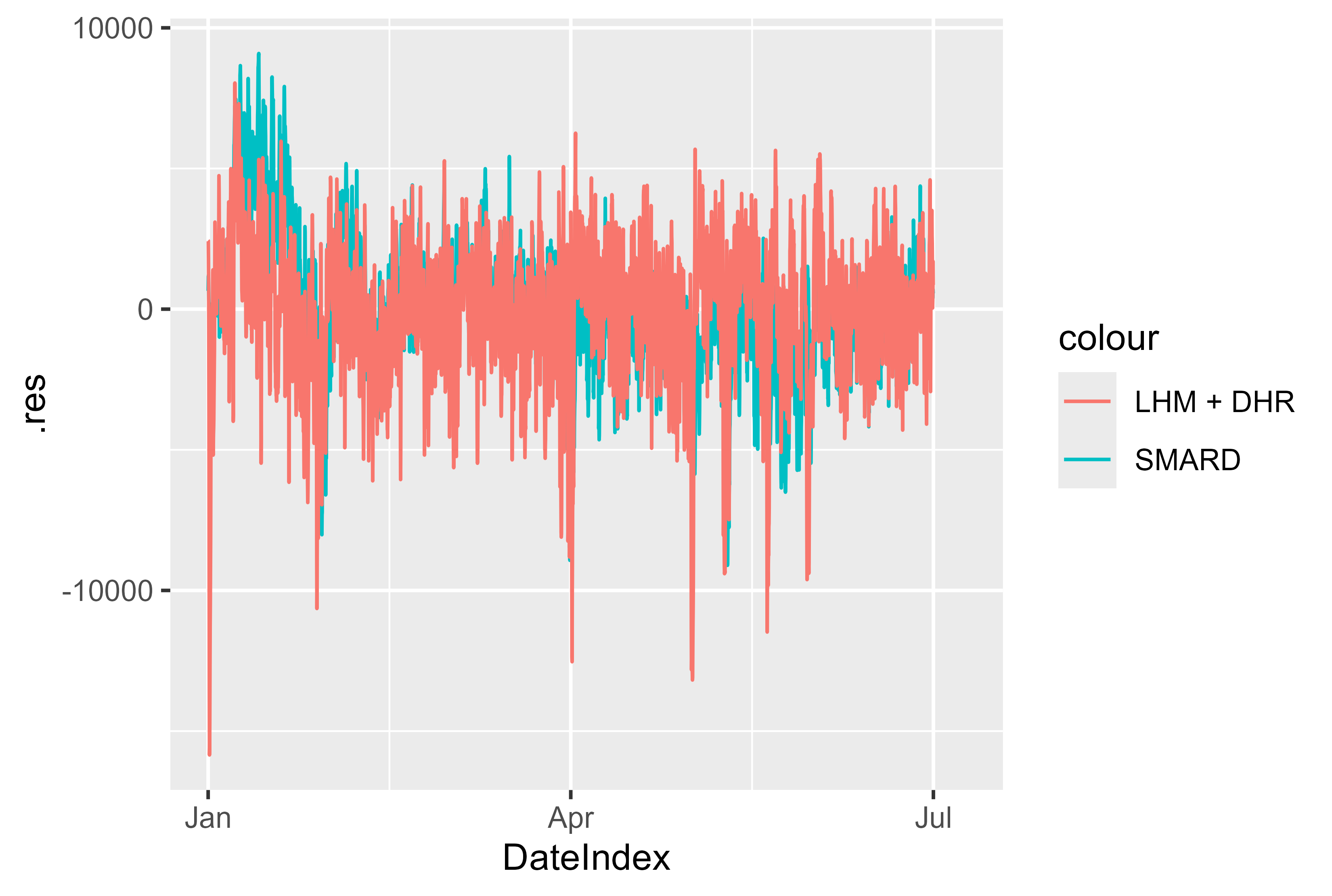الشكل 17 المتبقي LHM + DHR لشهر يناير - يوليو 2024
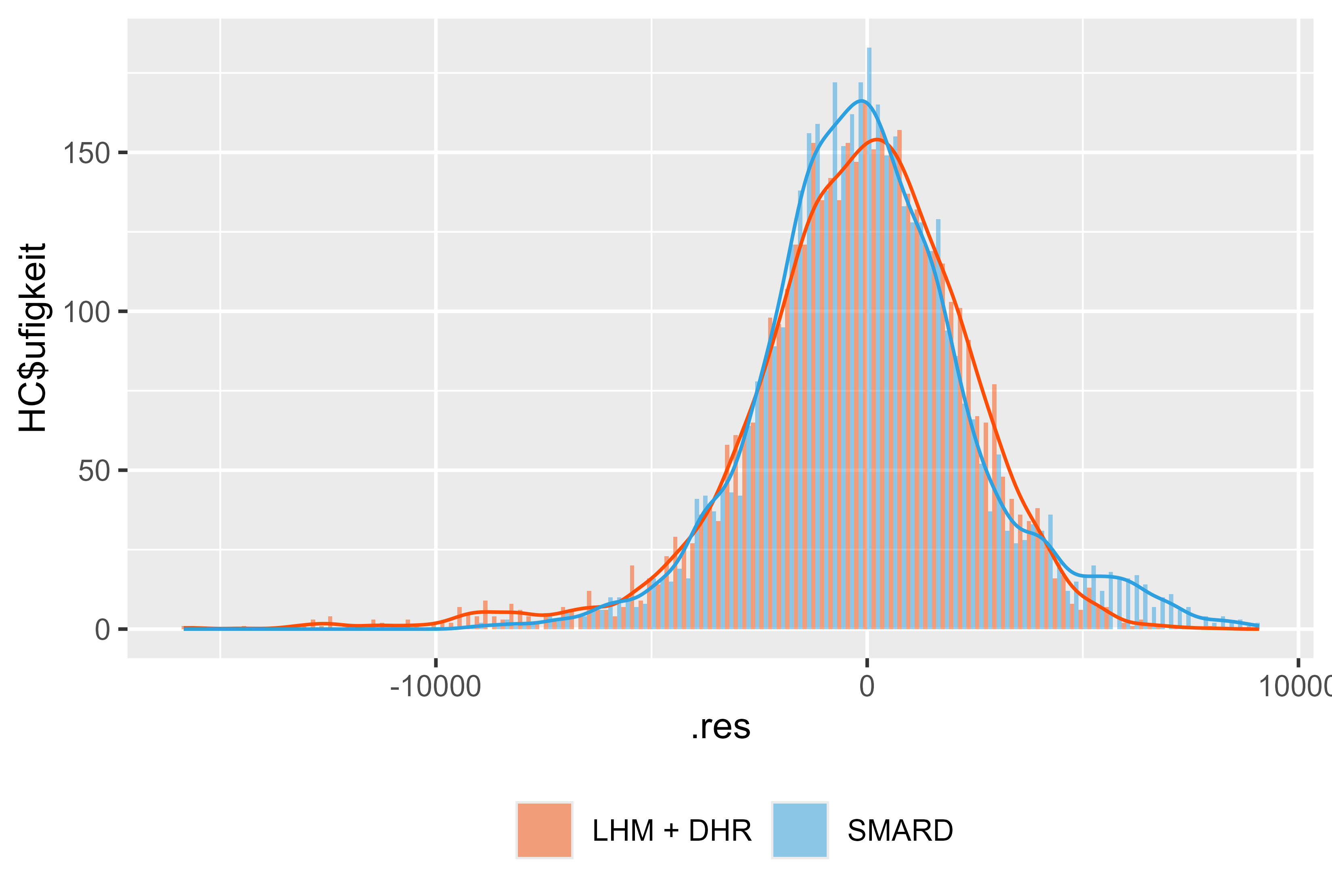الشكل 18 المتبقي LHM + DHR لشهر يناير - يوليو 2024
| فِهرِس | اسم النموذج | RMSE | ماب | ماي | مجمعة |
|---|---|---|---|---|---|
| 2 | ملاحظات حقيقية | 0.000 | 0.000000 | 0.000 | حقيقي |
| 3 | سمارد | 2480.693 | 3.602140 | 1869.466 | خطأ شنيع |
| 4 | سمارد | 2480.693 | 3.602140 | 1869.466 | حقيقي |
| 5 | version_5 | 2626.807 | 3.816012 | 1937.670 | حقيقي |
| 6 | version_0 | 2613.258 | 3.846888 | 1946.314 | حقيقي |
| 7 | version_7 | 2770.359 | 4.107272 | 2076.045 | حقيقي |
| 8 | version_8 | 2775.441 | 4.146788 | 2091.153 | حقيقي |
| 9 | version_9 | 2887.179 | 4.177841 | 2100.381 | حقيقي |
| 10 | version_6 | 2906.242 | 4.216517 | 2142.092 | حقيقي |
| 11 | arima_14_2021_2023.rds | 3208.735 | 4.389492 | 2207.395 | خطأ شنيع |
| 12 | arima_18_2021_2023.rds | 3208.735 | 4.389492 | 2207.395 | خطأ شنيع |
| 13 | version_4 | 2875.929 | 4.535388 | 2255.645 | حقيقي |
| 14 | version_2 | 2905.990 | 4.580770 | 2279.624 | حقيقي |
| 15 | arima_9_2021_2023.rds | 3267.160 | 4.611857 | 2302.918 | خطأ شنيع |
| 16 | arima_2_2021_2023.rds | 3251.390 | 4.614028 | 2301.447 | خطأ شنيع |
| 17 | arima_4_2021_2023.rds | 3251.390 | 4.614028 | 2301.447 | خطأ شنيع |
| 18 | arima_5_2021_2023.rds | 3251.390 | 4.614028 | 2301.447 | خطأ شنيع |
| 19 | arima_13_2021_2023.rds | 3283.745 | 4.619636 | 2307.415 | خطأ شنيع |
| 20 | arima_10_2021_2023.rds | 3265.913 | 4.625508 | 2314.395 | خطأ شنيع |
| 21 | arima_0_2021_2023.rds | 3269.009 | 4.645944 | 2317.138 | خطأ شنيع |
| 22 | arima_17_2021_2023.rds | 3269.009 | 4.645944 | 2317.138 | خطأ شنيع |
| 23 | arima_16_2021_2023.rds | 3298.902 | 4.673116 | 2334.857 | خطأ شنيع |
| 24 | arima_1_2021_2023.rds | 3312.429 | 4.696342 | 2340.193 | خطأ شنيع |
| 24 | Prophet_0_2021_2023.rds | 3044.849 | 4.711527 | 2435.572 | خطأ شنيع |
| 25 | arima_8_2021_2023.rds | 3332.217 | 4.716612 | 2358.085 | خطأ شنيع |
| 26 | arima_11_2021_2023.rds | 3358.020 | 4.758970 | 2388.791 | خطأ شنيع |
| 27 | arima_12_2021_2023.rds | 3430.191 | 5.022772 | 2495.067 | خطأ شنيع |
| 28 | arima_7_2021_2023.rds | 3475.671 | 5.049287 | 2510.903 | خطأ شنيع |
| 29 | version_3 | 3546.729 | 5.064654 | 2570.530 | حقيقي |
| 30 | arima_15_2021_2023.rds | 3734.584 | 5.165147 | 2606.661 | خطأ شنيع |
| 31 | arima_6_2021_2023.rds | 3748.583 | 5.375326 | 2723.837 | خطأ شنيع |
| 32 | version_1 | 4495.568 | 6.483477 | 3229.647 | حقيقي |
| 33 | arima_3_2021_2023.rds | 4558.982 | 6.953247 | 3453.387 | خطأ شنيع |
| 34 | tslm_0_2021_2023.rds | 6760.994 | 11.189119 | 5694.949 | خطأ شنيع |
| 35 | mean_2021_2023.rds | 9489.303 | 16.406032 | 8101.476 | خطأ شنيع |
| 36 | naive_2021_2023.rds | 14699.338 | 20.797370 | 12130.587 | خطأ شنيع |
| 37 | Drift_2021_2023.rds | 14763.692 | 20.917883 | 12200.002 | خطأ شنيع |
ملحوظة:
تحقق من المثال/ensemble_model_2022_forecast أو example/ensemble_model_2023_forecast
يمكننا تضمين المزيد من العوامل مثل:
