@article{chen2020neurodiffeq,
title={NeuroDiffEq: A Python package for solving differential equations with neural networks},
author={Chen, Feiyu and Sondak, David and Protopapas, Pavlos and Mattheakis, Marios and Liu, Shuheng and Agarwal, Devansh and Di Giovanni, Marco},
journal={Journal of Open Source Software},
volume={5},
number={46},
pages={1931},
year={2020}
}هل تعلم أن neurodiffeq يدعم حزم الحلول ويمكن استخدامه لحل المشكلات العكسية؟ انظر هنا!
؟ هل أنت على دراية بـ neurodiffeq؟ ؟ انتقل إلى الأسئلة الشائعة.
neurodiffeq عبارة عن حزمة لحل المعادلات التفاضلية مع الشبكات العصبية. المعادلات التفاضلية هي معادلات تربط بعض الوظائف بمشتقاتها. تظهر في مختلف المجالات العلمية والهندسية. تقليديا، يمكن حل هذه المشاكل عن طريق الطرق العددية (على سبيل المثال، الفرق المحدود، العناصر المحدودة). في حين أن هذه الأساليب فعالة وكافية، إلا أن إمكانية التعبير عنها محدودة بتمثيل وظيفتها. سيكون من المثير للاهتمام أن نتمكن من حساب حلول المعادلات التفاضلية المتصلة والقابلة للاشتقاق.
باعتبارها تقريبية للدالة العالمية، فقد ثبت أن الشبكات العصبية الاصطناعية لديها القدرة على حل المعادلات التفاضلية العادية (ODEs) والمعادلات التفاضلية الجزئية (PDEs) مع شروط أولية/حدية معينة. الهدف من neurodiffeq هو تنفيذ هذه التقنيات الحالية لاستخدام ANN لحل المعادلات التفاضلية بطريقة تسمح للبرنامج بأن يكون مرنًا بدرجة كافية للعمل على نطاق واسع من المشكلات التي يحددها المستخدم.
مثل معظم المكتبات القياسية، تتم استضافة neurodiffeq على PyPI. لتثبيت أحدث إصدار مستقر،
pip install -U neurodiffeq # '-U' يعني التحديث إلى الإصدار الأحدث
وبدلاً من ذلك، يمكنك تثبيت المكتبة يدويًا للوصول المبكر إلى ميزاتنا الجديدة. هذه هي الطريقة الموصى بها للمطورين الذين يرغبون في المساهمة في المكتبة.
git clone https://github.com/NeuroDiffGym/neurodiffeq.gitcd neurodiffeq && متطلبات تثبيت النقطة -r تثبيت النقطة. # لإجراء تغييرات على المكتبة، استخدم `pip install -e .`pytest tests/ # تشغيل الاختبارات. خياري.
نحن سعداء لمساعدتك في أي أسئلة. وفي هذه الأثناء، يمكنك الاطلاع على الأسئلة الشائعة.
لعرض البرامج التعليمية والوثائق الكاملة لـ neurodiffeq ، يرجى مراجعة الوثائق الرسمية.
بالإضافة إلى الوثائق، قمنا مؤخرًا بعمل فيديو توضيحي سريع باستخدام الشرائح.
من neurodiffeq استيراد difffrom neurodiffeq.solvers استيراد Solver1D، Solver2Dfrom neurodiffeq.conditions استيراد IVP، DirichletBVP2Dfrom neurodiffeq.networks استيراد FCNN، SinActv
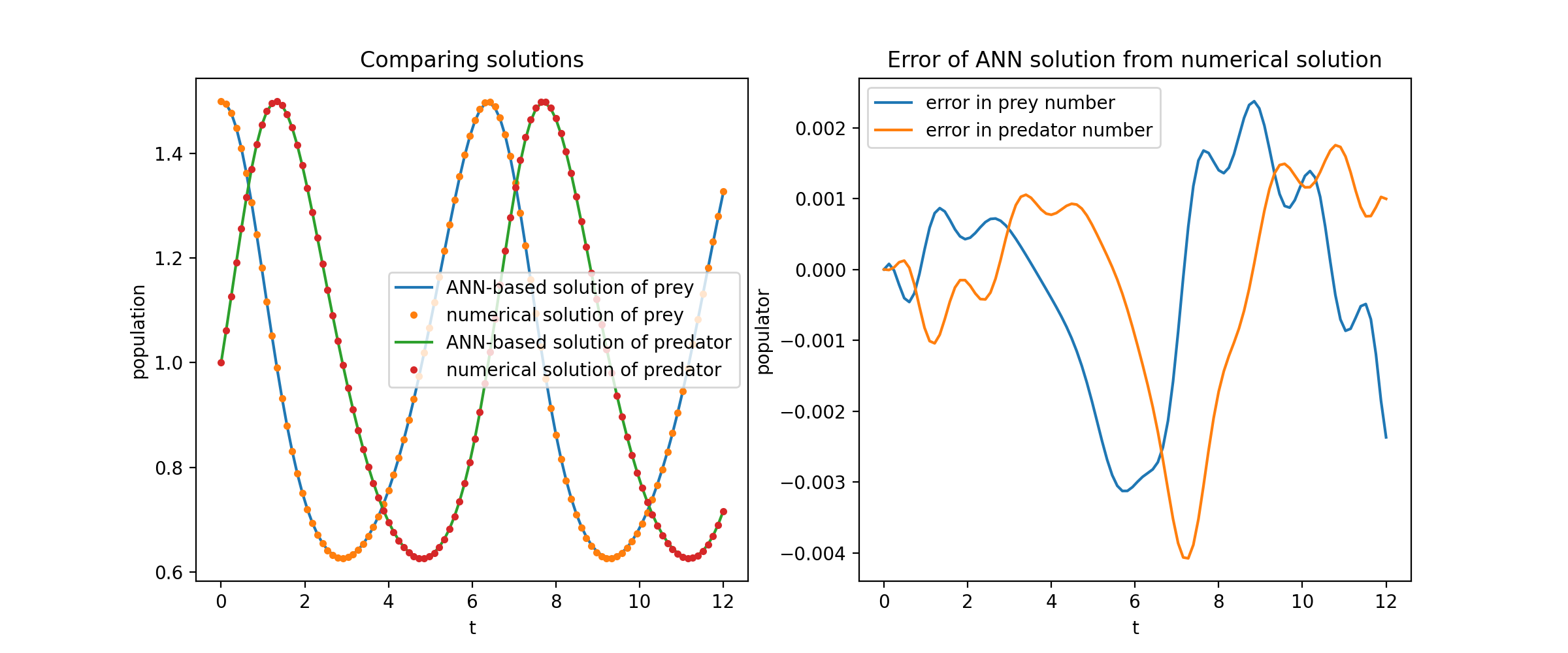
نحن هنا نحل نظامًا غير خطي يتكون من اثنين من المعادلات التفاضلية التفاضلية، المعروفة باسم معادلات لوتكا-فولتيرا. هناك دالتان غير معروفتين ( u و v ) ومتغير مستقل واحد ( t ).
Def ode_system(u, v, t): إرجاع [diff(u,t)-(uu*v), diff(v,t)-(u*vv)]الشروط = [IVP(t_0=0.0, u_0=1.5 ), IVP(t_0=0.0, u_0=1.0)]nets = [FCNN(actv=SinActv), FCNN(actv=SinActv)]حلاً = Solver1D(ode_system, الشروط, t_min=0.1, t_max=12.0, nets=nets)solver.fit(max_epochs=3000)solution =solver.get_solution()
solution هو كائن قابل للاستدعاء، يمكنك تمرير صفائف numpy أو موترات الشعلة إليه مثل
u, v =solution(t, to_numpy=True) # t يمكن أن يكون np.ndarray أو torch.Tensor
يؤدي رسم u و v مقابل حلولهما التحليلية إلى الحصول على شيء مثل:
نحن هنا نحل معادلة لابلاس مع شروط حدود ديريشليت على المستطيل. لاحظ أننا نختار معادلة لابلاس لبساطتها في الحل التحليلي الحسابي. من الناحية العملية، يمكنك تجربة أي أجهزة PDE غير خطية وفوضوية ، بشرط ضبط أداة الحل جيدًا بما فيه الكفاية.
حل نظام PDE ثنائي الأبعاد يشبه إلى حد كبير حل المعادلات التفاضلية التفاضلية (ODEs)، باستثناء وجود متغيرين x و y لمسائل القيمة الحدية أو x و t لمسائل القيمة الحدية الأولية، وكلاهما مدعوم.
def pde_system(u, x, y):return [diff(u, x, order=2) + diff(u, y, order=2)]conditions = [DirichletBVP2D(x_min=0, x_min_val=lambda y: torch. الخطيئة (np.pi*y)،x_max=1، x_max_val=لامدا ص: 0، y_min=0، y_min_val=لامدا س: 0، y_max=1، y_max_val=لامدا س: 0،
)
]شبكات = [FCNN(n_input_units=2, n_output_units=1, Hidden_units=(512,))]حل = Solver2D(pde_system, الشروط, xy_min=(0, 0), xy_max=(1, 1), nets=nets) Solver.fit(max_epochs=2000)الحل =solver.get_solution() يختلف توقيع solution لـ 2D PDE قليلاً عن توقيع ODE. مرة أخرى، يستغرق الأمر إما مصفوفات numpy أو موترات الشعلة.
u = الحل (x، y، to_numpy = صحيح)
يؤدي تقييم u على [0,1] × [0,1] إلى الحصول على المخططات التالية
| الحل القائم على ANN | المتبقية من PDE |
|---|---|
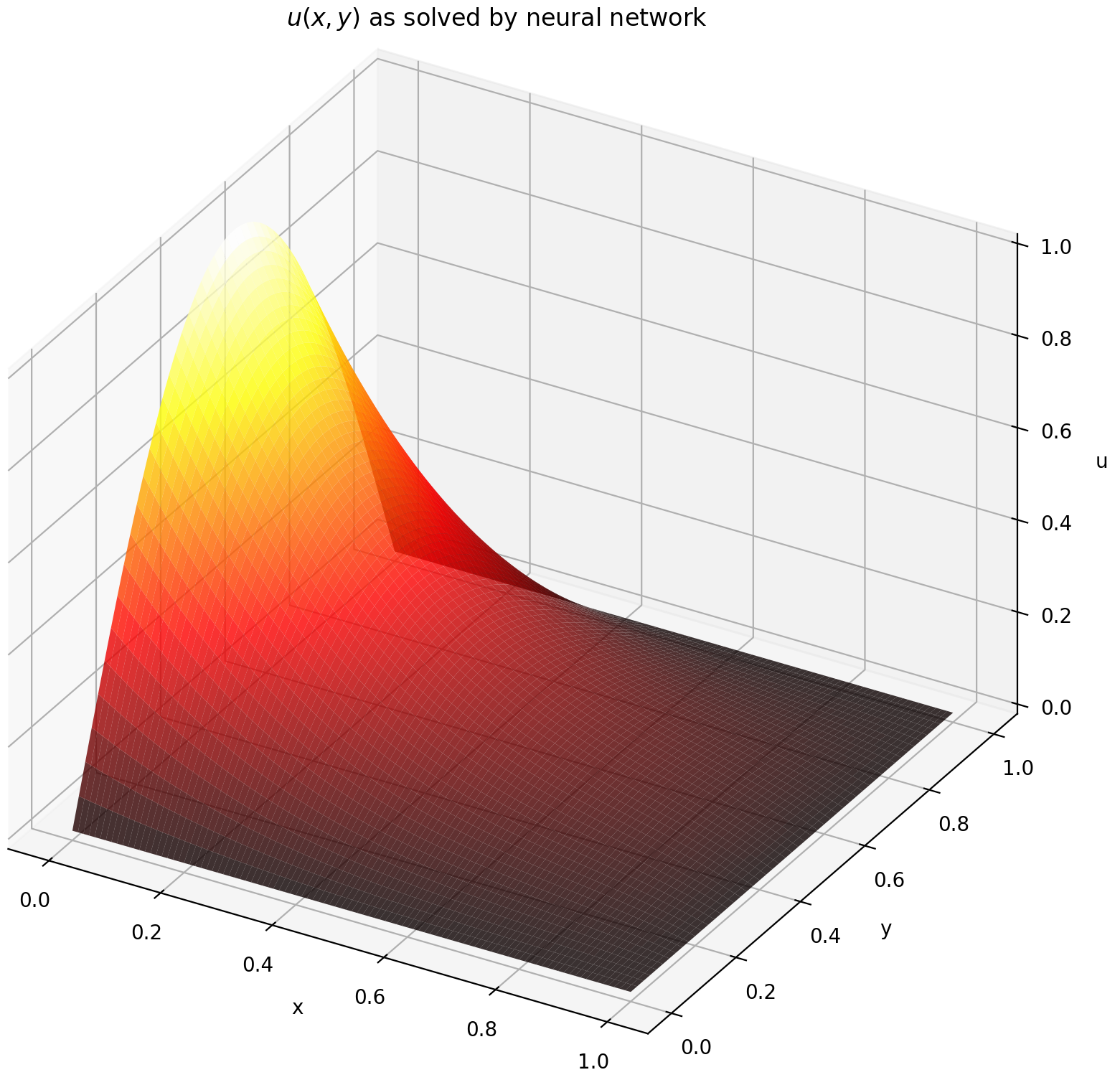 | 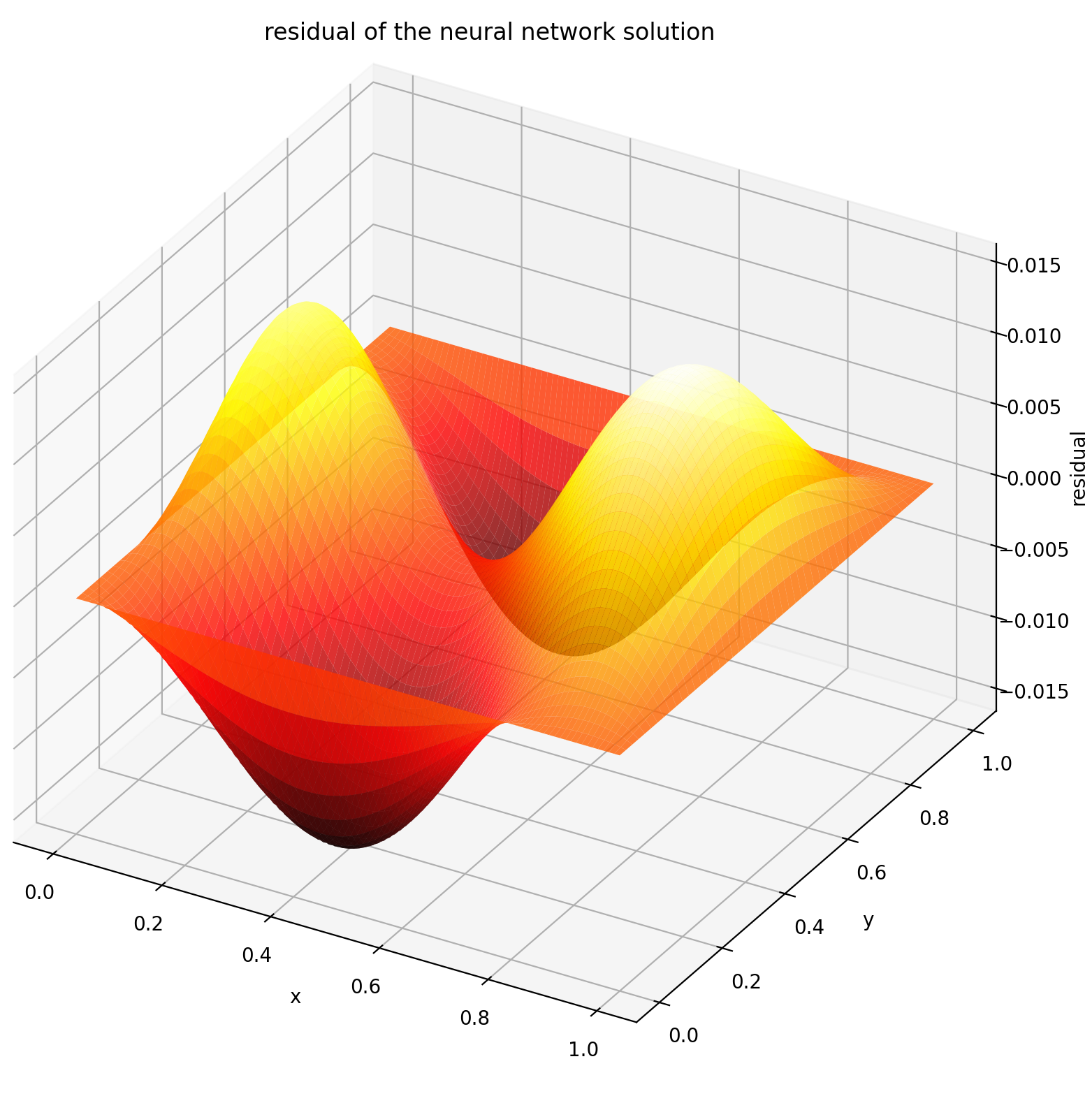 |
تعد الشاشة أداة لتصور حلول PDE/ODE بالإضافة إلى تاريخ الخسارة والمقاييس المخصصة أثناء التدريب. يحتاج مستخدمو Jupyter Notebooks إلى تشغيل %matplotlib notebook السحري. بالنسبة لمستخدمي Jupyter Lab، جرب %matplotlib widget .
من neurodiffeq.monitors استيراد Monitor1D...monitor = Monitor1D(t_min=0.0, t_max=12.0, check_every=100)solver.fit(..., callbacks=[monitor.to_callback()])
من المفترض أن تشاهد المخططات يتم تحديثها كل 100 عصر وكذلك في العصر الأخير ، مع عرض مخططين - أحدهما لتصور الحل على الفاصل الزمني [0,12] والآخر لسجل الخسارة (التدريب والتحقق من الصحة).
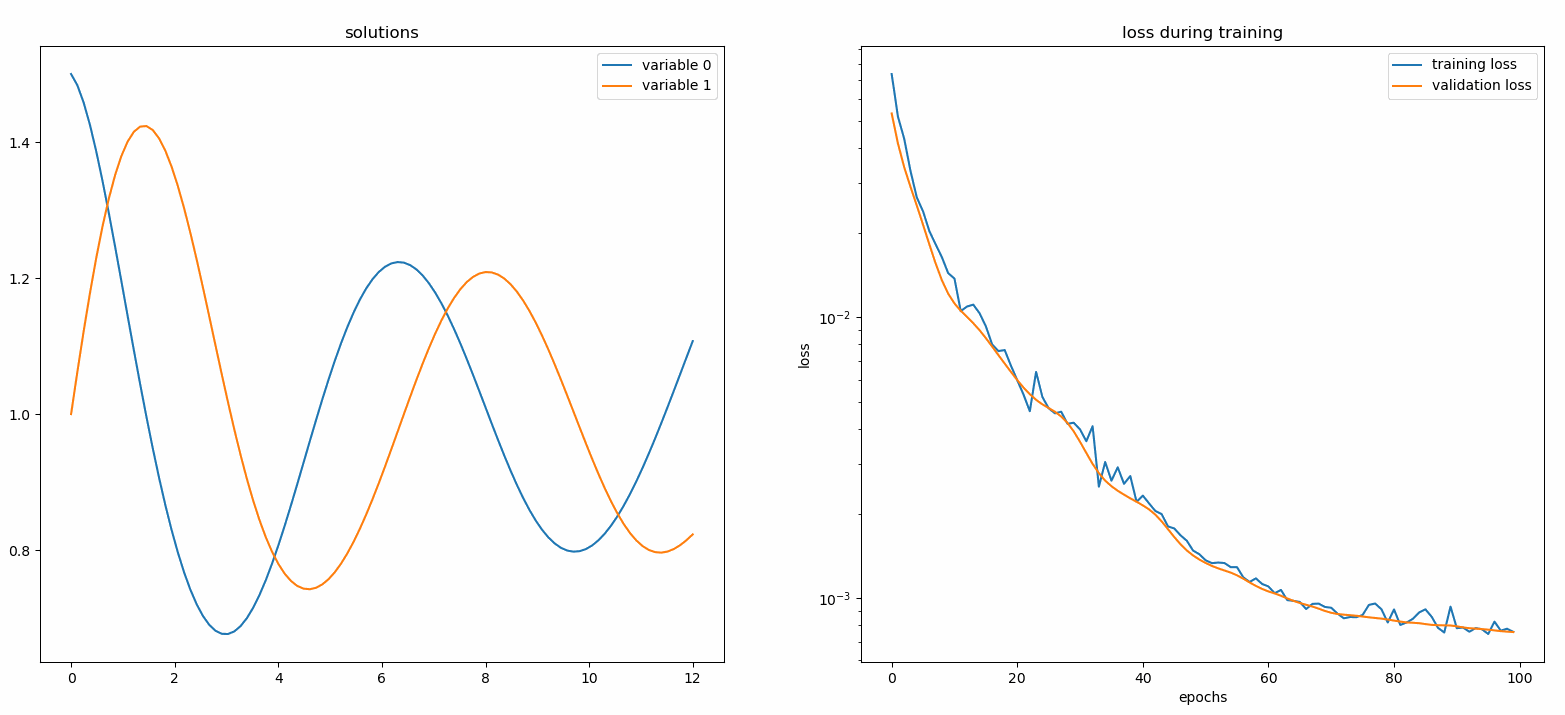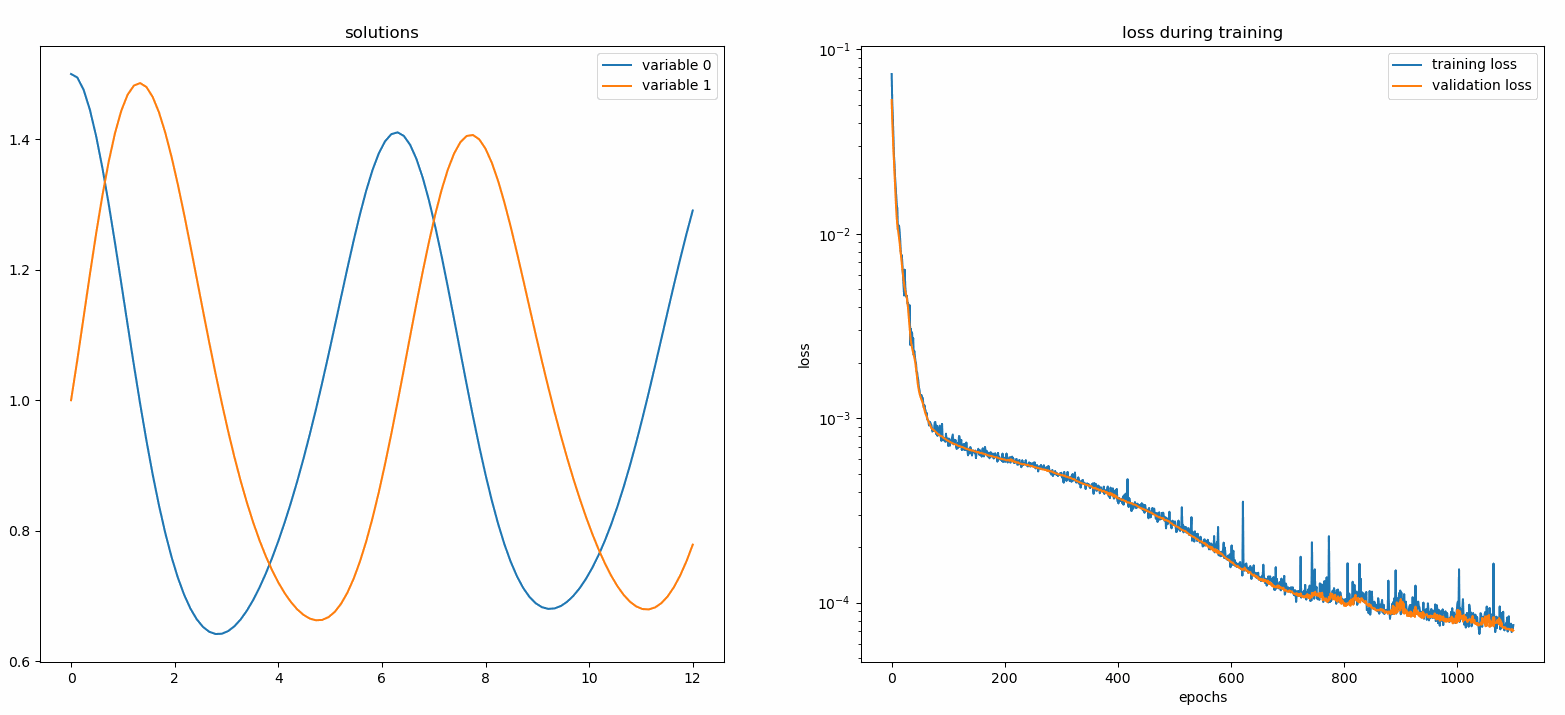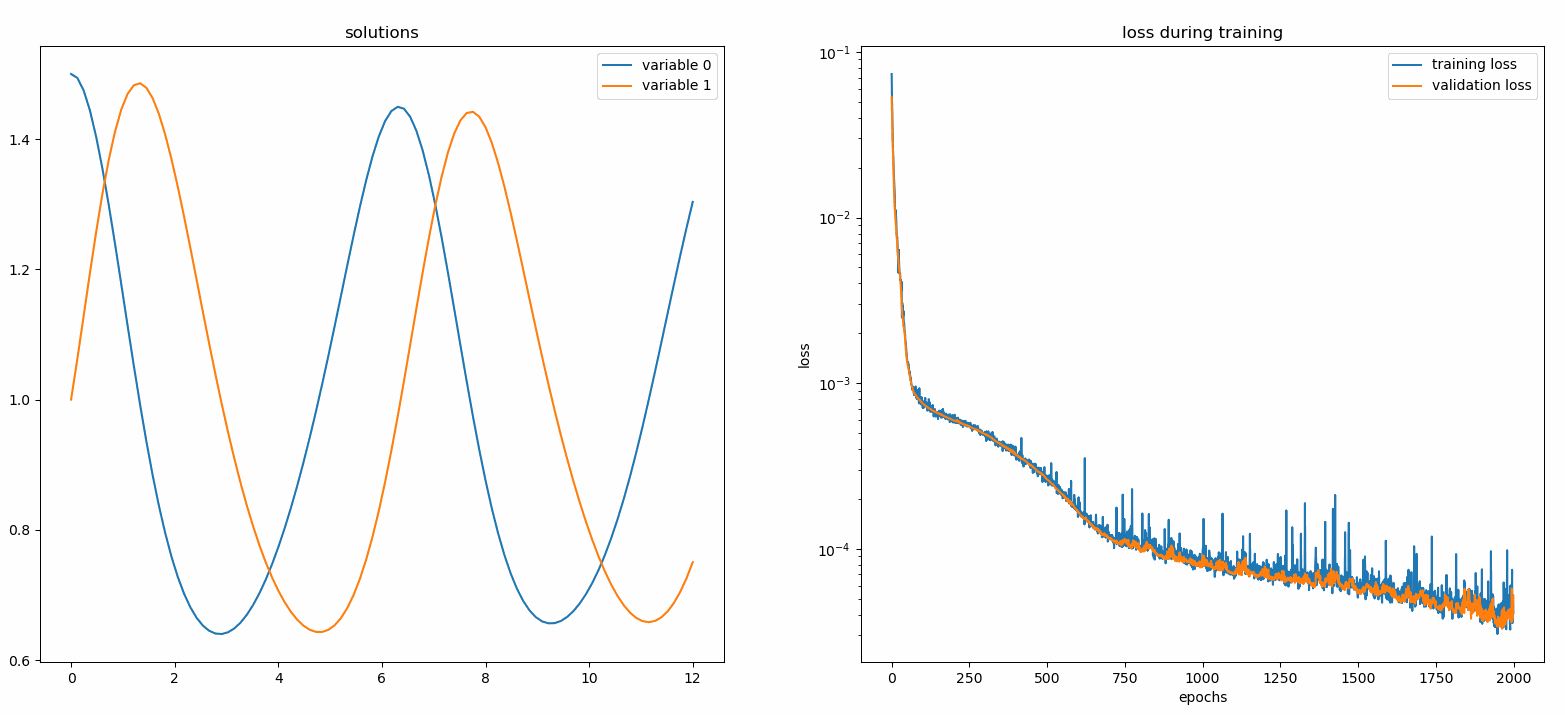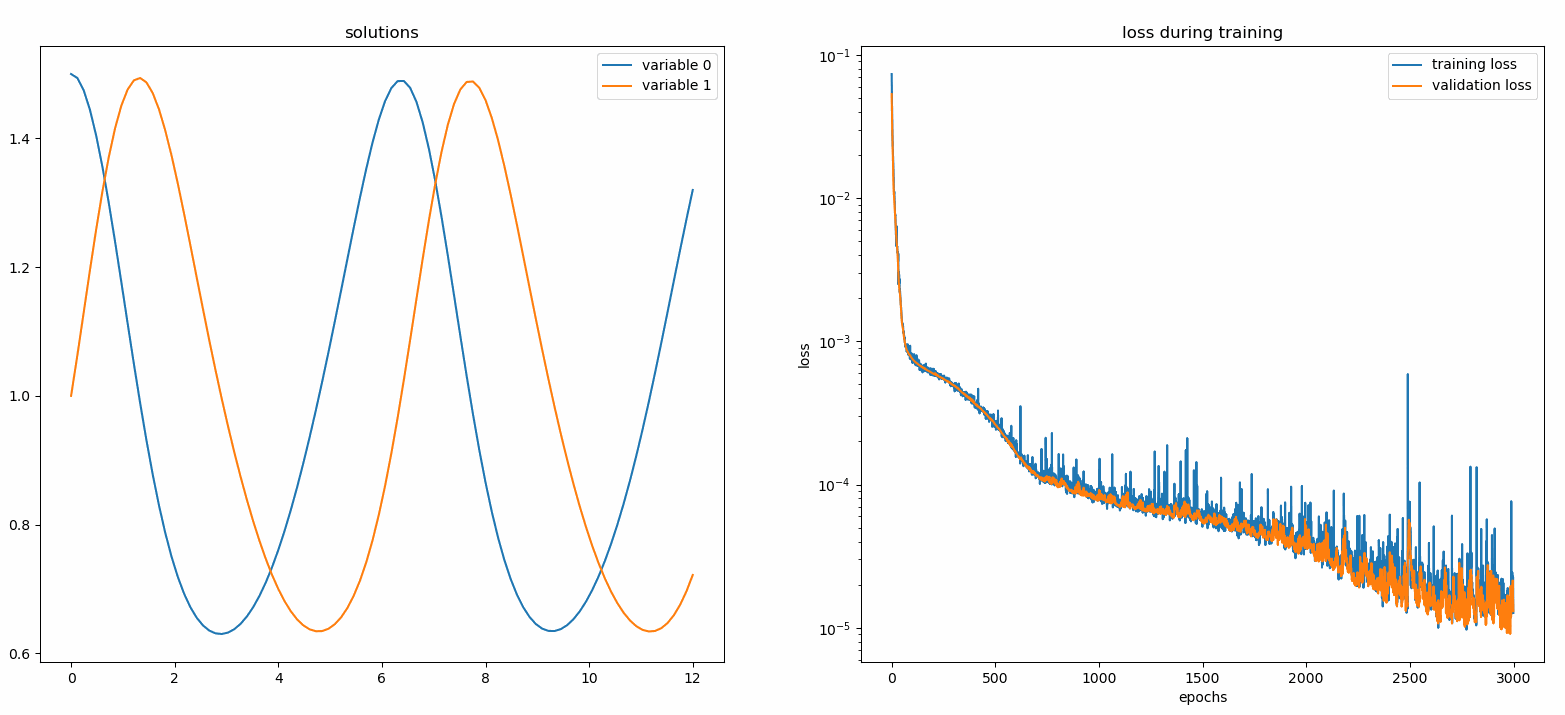
من أجل الراحة، قمنا بتنفيذ شبكة عصبية FCNN - متصلة بالكامل، والتي يمكن تخصيص وحداتها المخفية ووظائف التنشيط.
من neurodiffeq.networks import FCNN# الافتراضي: n_input_units=1, n_output_units=1, Hidden_units=[32, 32],activation=torch.nn.Tanhnet1 = FCNN(n_input_units=..., n_output_units=..., Hidden_units=[ ...، ...، ...]، التنشيط=...) ...شبكات = [net1، net2، ...]
عادة ما تكون FCNN نقطة انطلاق جيدة. بالنسبة للمستخدمين المتقدمين، تتوافق أدوات الحل مع أي torch.nn.Module مخصص. القيود الوحيدة هي:
تأخذ الوحدات موتر الشكل (None, n_coords) وتخرج موتر الشكل (None, 1) .
يجب أن يكون هناك إجمالي وحدات n_funcs في nets ليتم تمريرها إلى solver = Solver(..., nets=nets) .
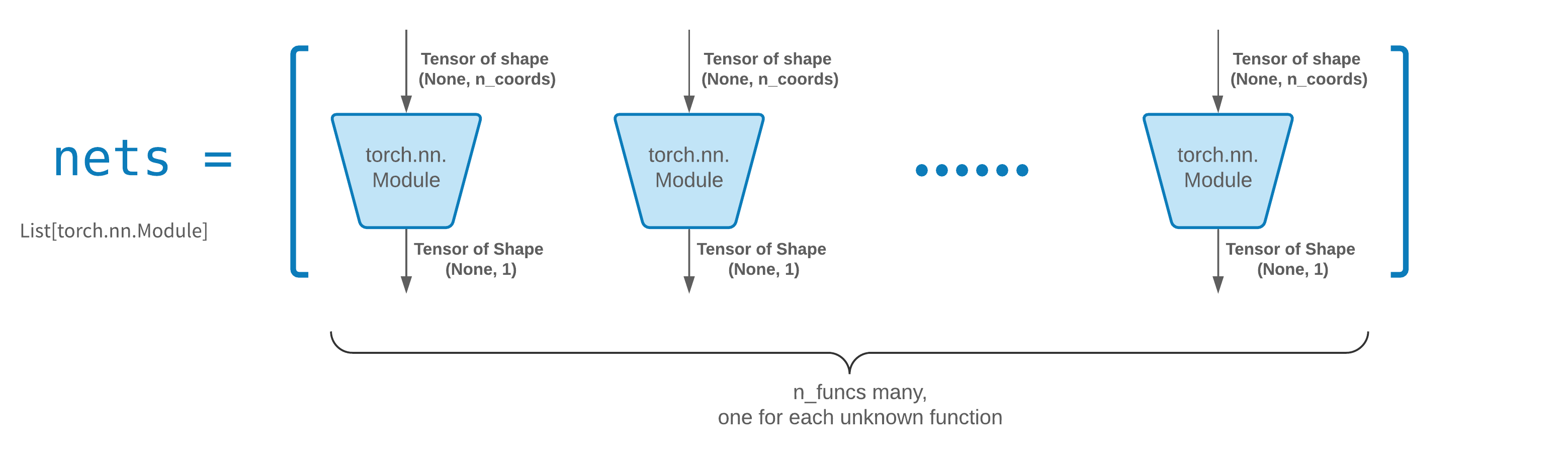
في الواقع، لدى neurodiffeq ميزة Single_net لا تلتزم بالقواعد المذكورة أعلاه، والتي لن يتم تغطيتها هنا.
اقرأ البرنامج التعليمي لـ PyTorch حول إنشاء بنية الشبكة الخاصة بك (المعروفة أيضًا باسم الوحدة النمطية).
يتم نقل التعلم بسهولة عن طريق إجراء تسلسل old_solver.nets (قائمة وحدات الشعلة) إلى القرص ثم تحميلها وتمريرها إلى حل جديد:
old_solver.fit(max_epochs=...)# ... تفريغ `old_solver.nets` إلى القرص# ... تحميل الشبكات من القرص، وتخزينها في بعض `loaded_nets`variablenew_solver = Solver(..., nets=loaded_nets )new_solver.fit(max_epochs=...)
نحن نعمل حاليًا على وظائف المجمع لحفظ/تحميل الشبكات والمتغيرات الداخلية الأخرى لـ Solvers. في غضون ذلك، يمكنك قراءة البرنامج التعليمي لـ PyTorch حول حفظ وتحميل شبكاتك.
في neurodiffeq، يتم تدريب الشبكات عن طريق تقليل الخسارة (بقايا ODE/PDE) التي يتم تقييمها على مجموعة من النقاط في المجال. يتم إعادة تشكيل النقاط بشكل عشوائي في كل مرة. للتحكم في عدد النقاط التي تم أخذ عينات منها وتوزيعها والمجال المحيط بها، يمكنك تحديد generator التدريب/التحقق الخاصة بك.
من neurodiffeq.generators import Generator1D# الافتراضي t_min=0.0، t_max=1.0،method='uniform'، Noise_std=Noneg1 = Generator1D(size=..., t_min=..., t_max=...,method=.. ., الضوضاء_std=...)g2 = Generator1D(size=..., t_min=..., t_max=..., الطريقة=..., الضوضاء_std=...)حل = Solver1D(..., Train_generator=g1, valid_generator=g2)
فيما يلي بعض نماذج توزيعات Generator1D .
Generator1D(8192, 0.0, 1.0, method='uniform') | Generator1D(8192, -1.0, 0.0, method='log-spaced-noisy', noise_std=1e-3) |
|---|---|
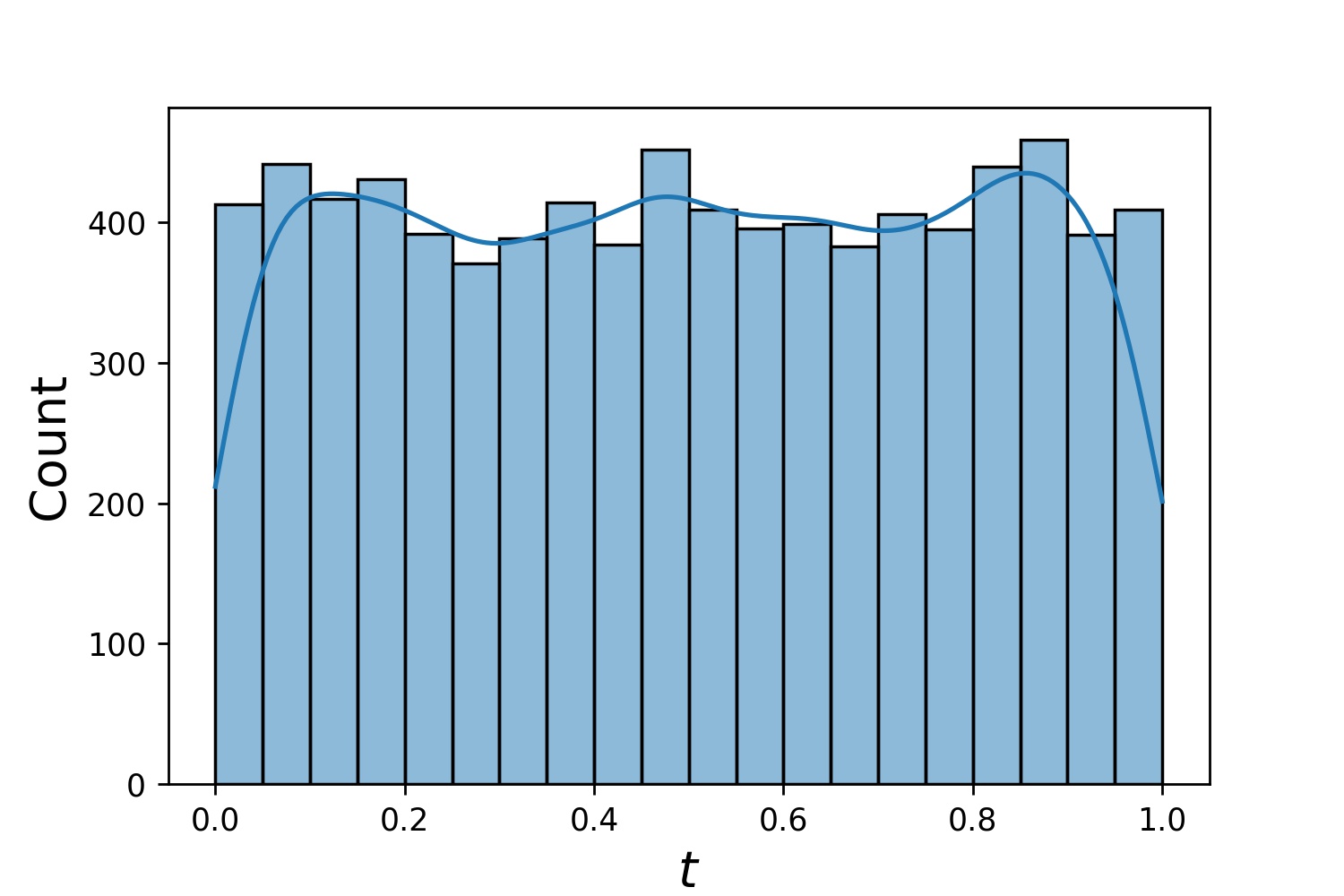 | 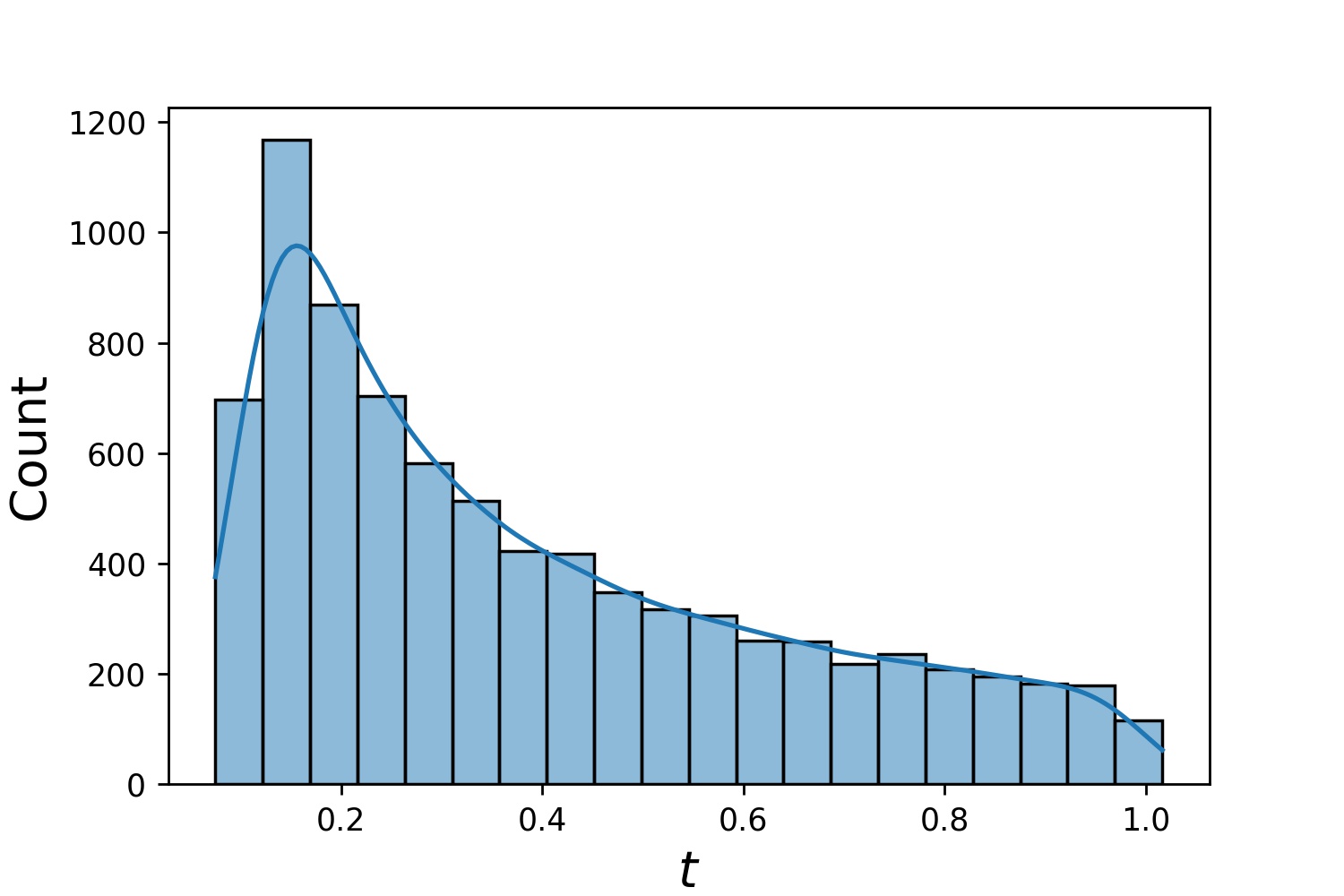 |
لاحظ أنه عند تحديد كل من train_generator و valid_generator ، يمكن حذف t_min و t_max في Solver1D(...) . في الواقع، حتى لو قمت بتمرير t_min و t_max و train_generator و valid_generator معًا، فسيتم تجاهل t_min و t_max .
ميزة أخرى رائعة للمولدات هي أنه يمكنك ربطها، على سبيل المثال
g1 = Generator2D((16, 16), xy_min=(0, 0), xy_max=(1, 1))g2 = Generator2D((16, 16), xy_min=(1, 1), xy_max=(2, 2) ))ز = g1 + g2
هنا، سيكون g هو المولد الذي يقوم بإخراج العينات المجمعة من g1 و g2
g1 | g2 | g1 + g2 |
|---|---|---|
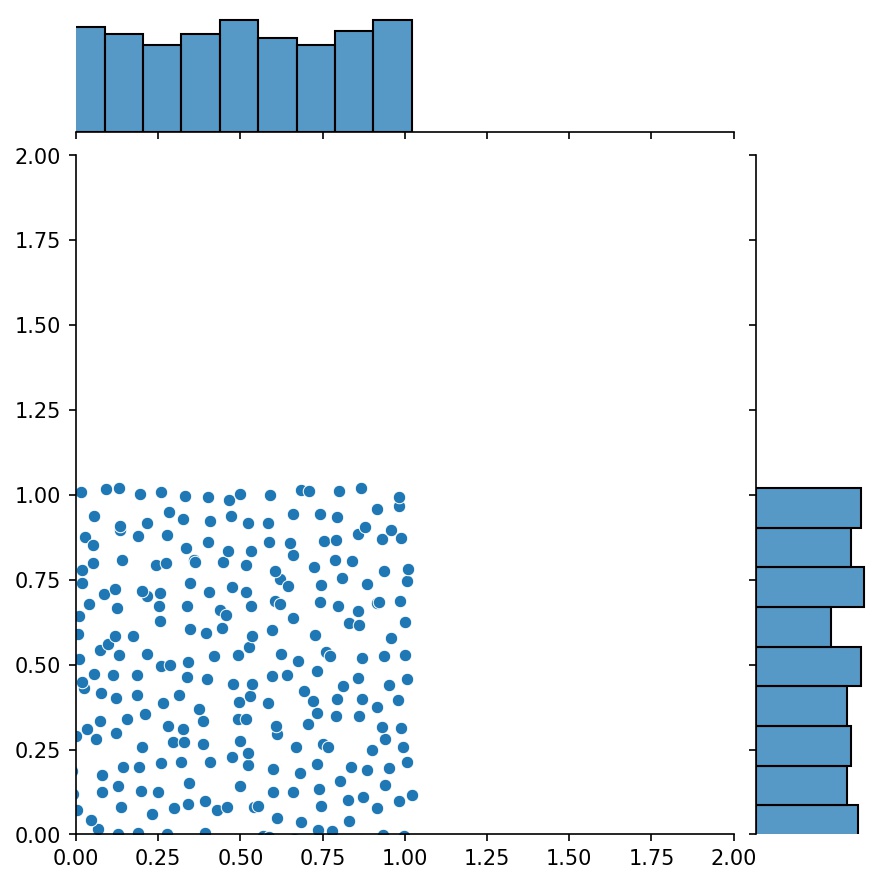 | 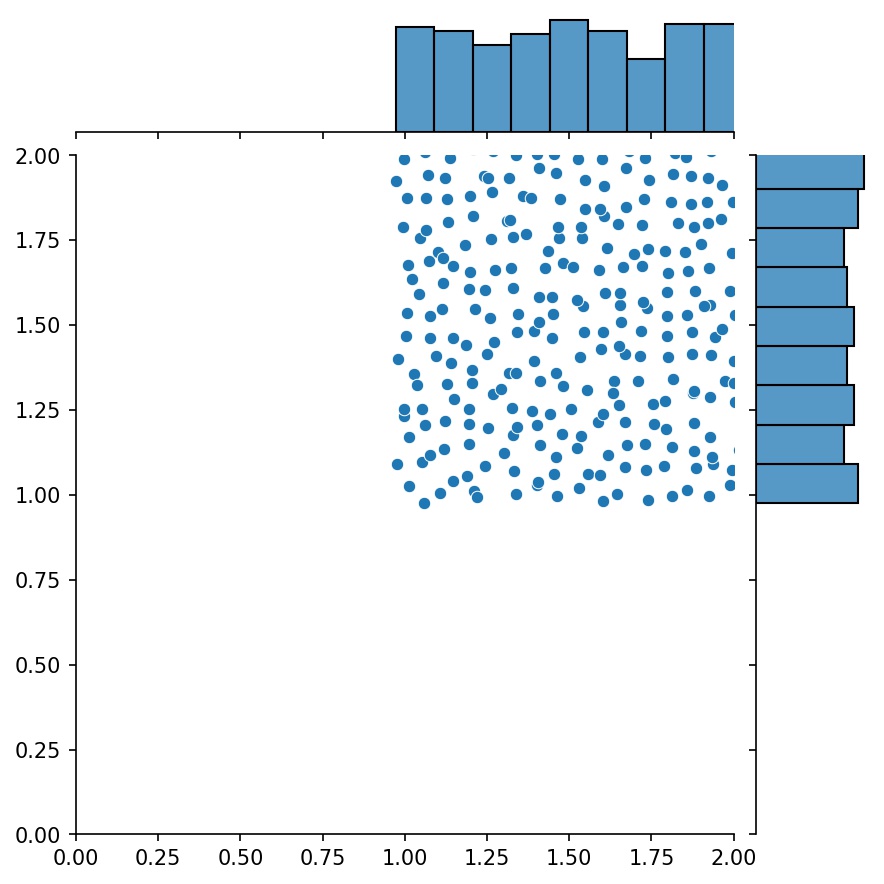 |  |
يمكنك استخدام Generator2D و Generator3D وما إلى ذلك لأخذ العينات في الأبعاد الأعلى. ولكن هناك أيضًا طريقة أخرى
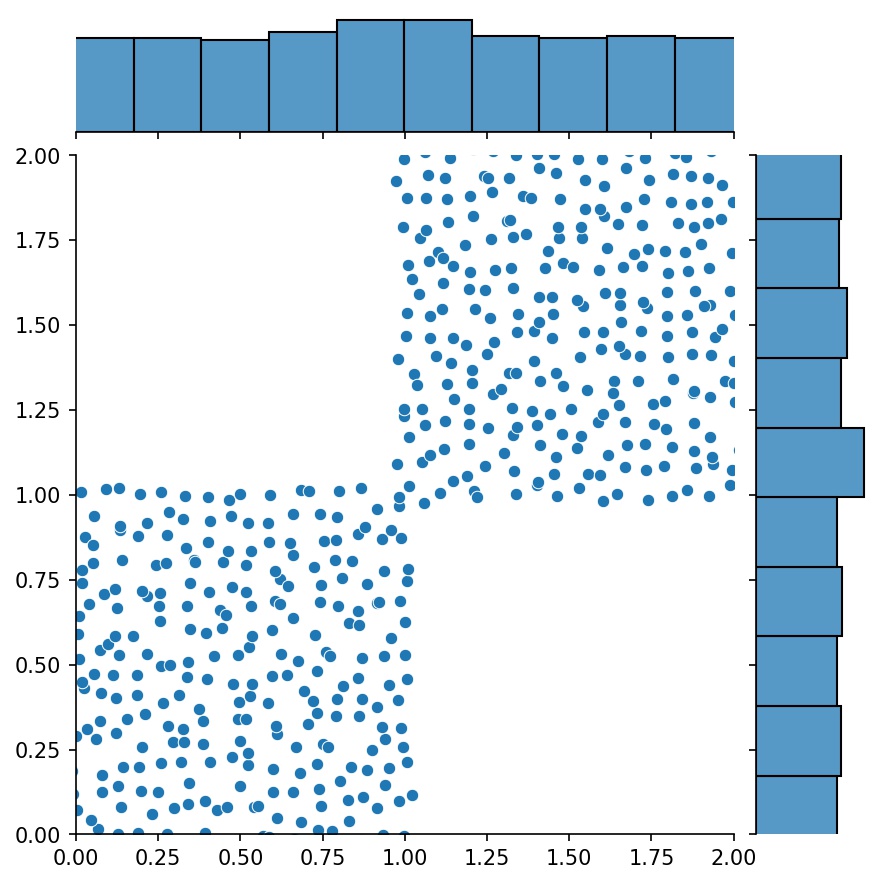
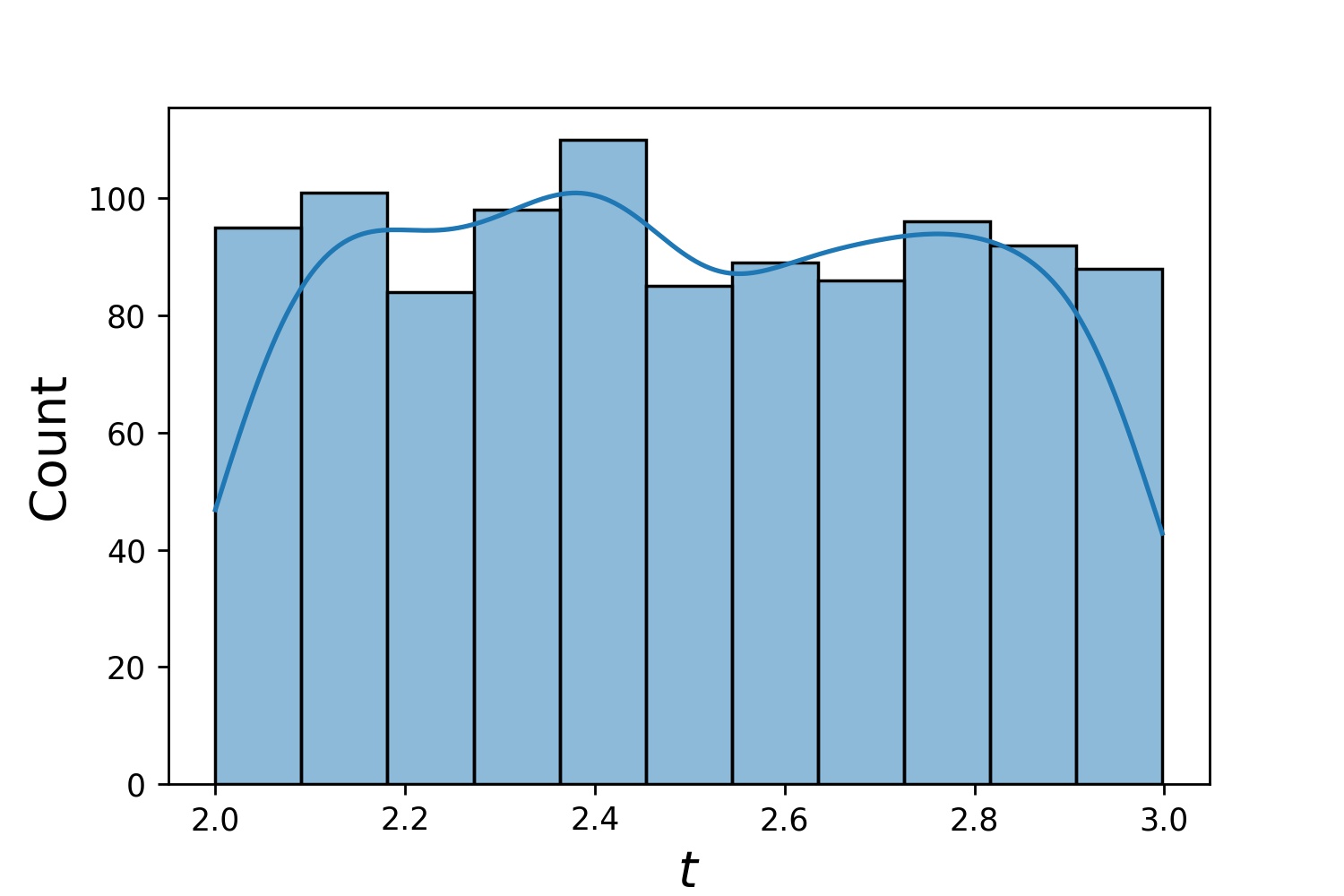
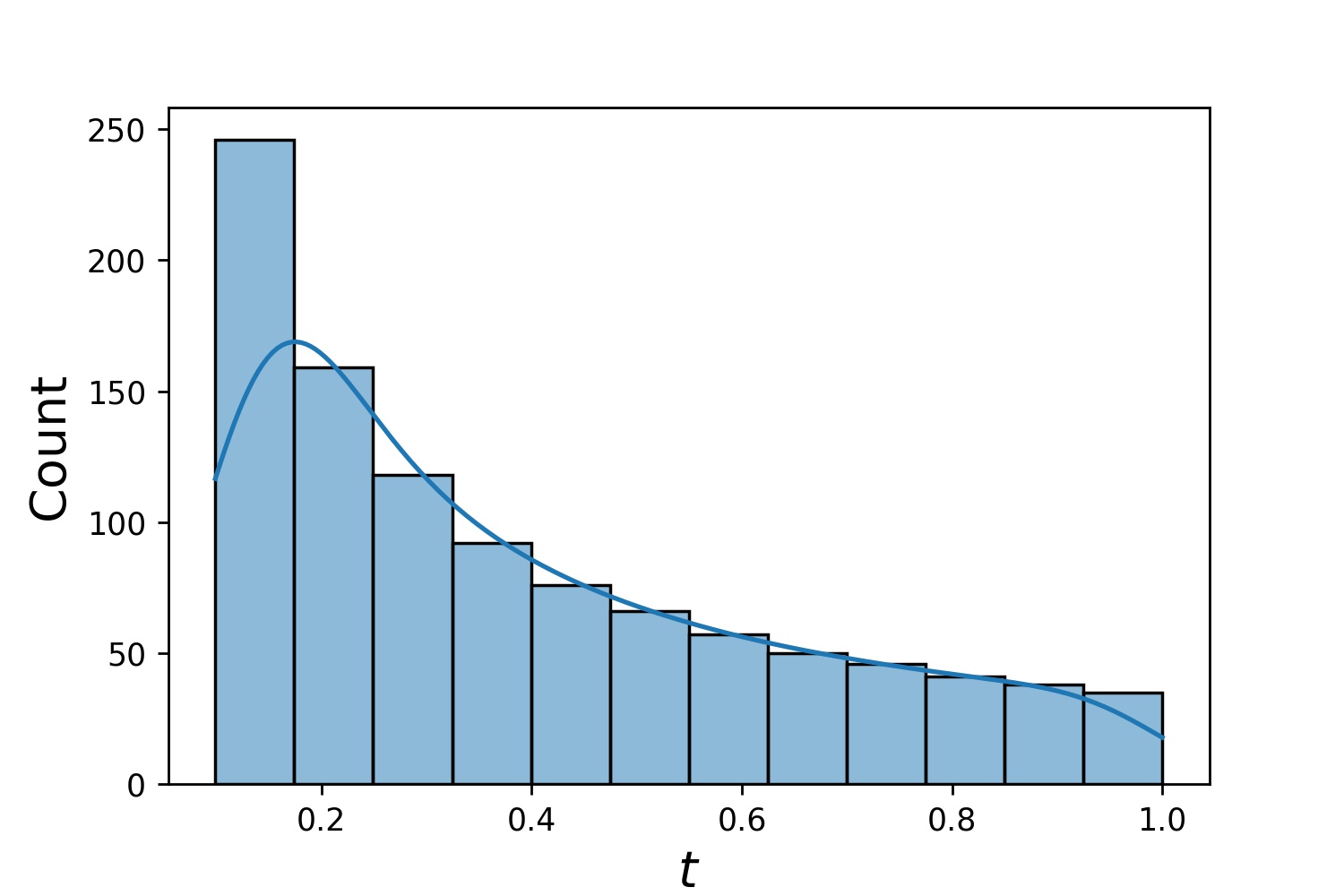
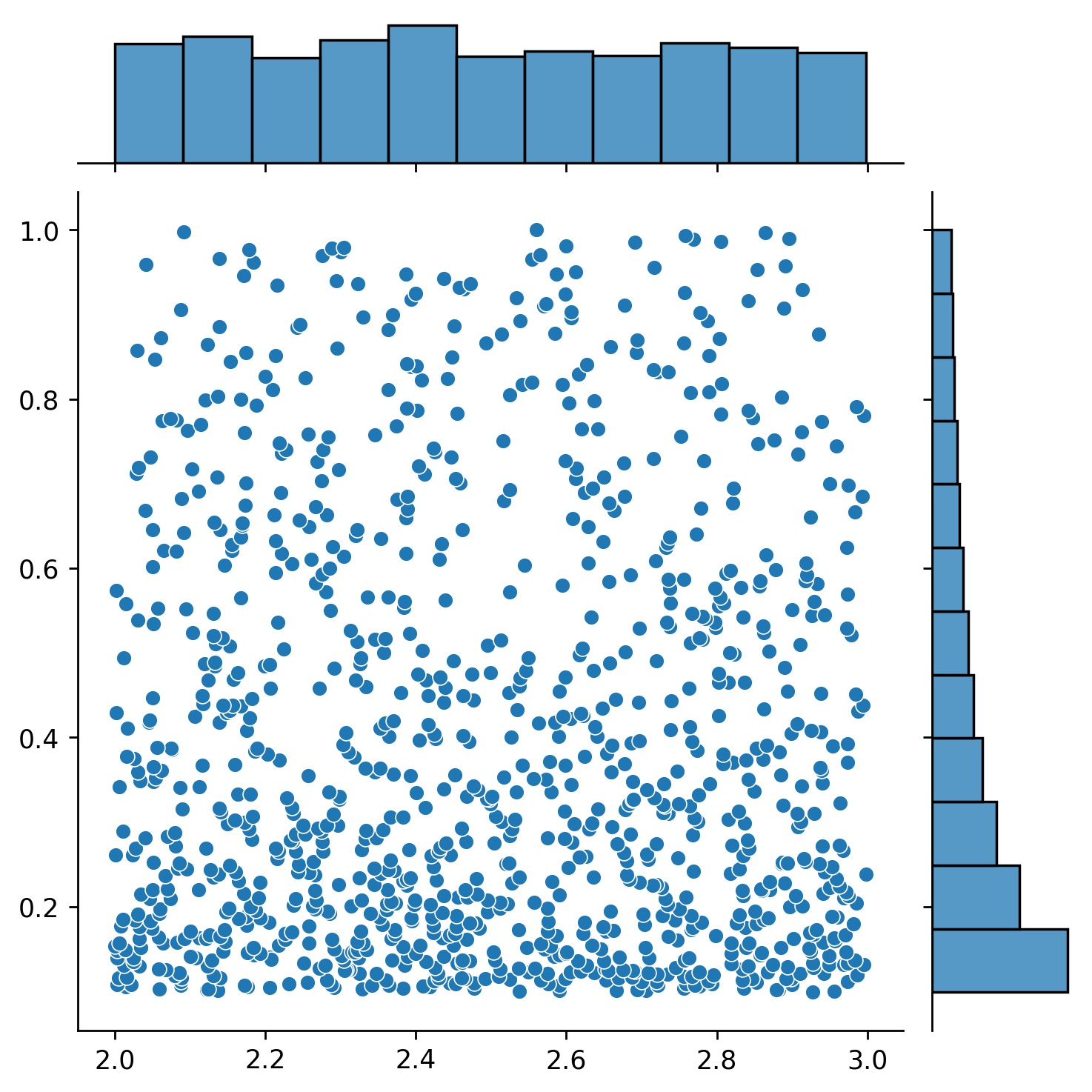
g1 = Generator1D(1024, 2.0, 3.0, طريقة='موحد')g2 = Generator1D(1024, 0.1, 1.0, طريقة='log-spaced-noisy', الضوضاء_std=0.001)g = g1 * g2
هنا، g سيكون مولدًا ينتج 1024 نقطة في مستطيل ثنائي الأبعاد (2,3) × (0.1,1) في كل مرة. يتم استخلاص إحداثيات x منها من (2,3) باستخدام إستراتيجية uniform والإحداثيات y مأخوذة من (0.1,1) باستخدام Strategy log-spaced-noisy .
g1 | g2 | g1 * g2 |
|---|---|---|
 |  |  |
في بعض الأحيان، يكون من المثير للاهتمام حل مجموعة من المعادلات مرة واحدة. على سبيل المثال، قد ترغب في حل المعادلات التفاضلية بالصيغة du/dt + λu = 0 تحت الشرط الأولي u(0) = U0 . قد ترغب في حل هذه المشكلة لكل من λ و U0 مرة واحدة، من خلال معاملتهم كمدخلات للشبكات العصبية.
أحد هذه التطبيقات هو التفاعلات الكيميائية، حيث يكون معدل التفاعل غير معروف. تتوافق معدلات التفاعل المختلفة مع حلول مختلفة، ويطابق حل واحد فقط نقاط البيانات المرصودة. ربما تكون مهتمًا أولاً بحل مجموعة من الحلول، ثم تحديد أفضل معدلات التفاعل (المعروفة أيضًا باسم معلمات المعادلة). تُعرف الخطوة الثانية بالمشكلة العكسية .
فيما يلي مثال لكيفية القيام بذلك باستخدام neurodiffeq :
لنفترض أن لدينا معادلة du/dt + λu = 0 والشرط الأولي u(0) = U0 حيث λ و U0 ثابتان غير معروفين. لدينا أيضًا مجموعة من الملاحظات t_obs و u_obs . نقوم أولاً باستيراد BundleSolver و BundleIVP وهو أمر ضروري للحصول على حزمة الحلول:
من neurodiffeq.conditions استيراد BundleIVPfrom neurodiffeq.solvers استيراد BundleSolver1Dimport matplotlib.pyplot كـ pltimport numpy مثل npimport torchfrom neurodiffeq import diff
نحدد مجال الإدخال t ، وكذلك مجال المعلمات λ و U0 . نحتاج أيضًا إلى اتخاذ قرار بشأن ترتيب المعلمات. وهي التي ينبغي أن تكون المعلمة الأولى، والتي ينبغي أن تكون الثانية. ولأغراض هذا العرض التوضيحي، نختار λ لتكون المعلمة الأولى (الفهرس 0)، و U0 لتكون المعلمة الثانية (الفهرس 1). من المهم جدًا تتبع مؤشرات المعلمات.
T_MIN، T_MAX = 0، 1LAMBDA_MIN، LAMBDA_MAX = 3، 5 # المعلمة الأولى، الفهرس = 0U0_MIN، U0_MAX = 0.2، 0.6 # المعلمة الثانية، الفهرس = 1
ثم نحدد conditions solver كالمعتاد، باستثناء أننا نستخدم BundleIVP و BundleSolver1D بدلاً من IVP و Solver1D . واجهة هذين الاثنين مشابهة جدًا لـ IVP و Solver1D . يمكنك معرفة المزيد في مرجع API.
# معلمات المعادلة تأتي بعد المدخلات (عادةً الإحداثيات الزمنية والمكانية)diff_eq = lambda u, t, lmd: [diff(u, t) + lmd * u]# يجب تسمية وسيطة الكلمة الرئيسية "u_0" في BundleIVP. إذا كنت تستخدم أي شيء آخر، على سبيل المثال `y0`، `u0`، وما إلى ذلك، فلن يعمل. الشروط = [BundleIVP(t_0=0, u_0=None, Bundle_param_lookup={'u_0': 1}) # u_0 لديه الفهرس 1] الحل = BundleSolver1D(ode_system=diff_eq,conditions=conditions,t_min=T_MIN, t_max=T_MAX, theta_min=[LAMBDA_MIN, U0_MIN], # lect له فهرس 0; معلمة المعادلة، التي تحتوي على فهرس 0n_batches_valid=1،
) نظرًا لأن λ هي معلمة في المعادلة و U0 هي معلمة في الحالة الأولية ، فيجب علينا تضمين λ في diff_eq و U0 في الحالة. إذا كانت المعلمة موجودة في كل من المعادلة والشرط، فيجب تضمينها في كلا المكانين. يجب أن تكون جميع عناصر conditions التي تم تمريرها إلى BundleSovler1D عبارة عن شروط Bundle* ، حتى لو لم تكن تحتوي على معلمات.
الآن، يمكننا تدريبه والحصول على الحل كما نفعل عادةً.
Solver.fit(max_epochs=1000)الحل =solver.get_solution(الأفضل=صحيح)
يتوقع الحل وجود ثلاثة مدخلات - t و λ و U0 . يجب أن يكون لجميع المدخلات نفس الشكل. على سبيل المثال، إذا كنت مهتمًا بتثبيت λ=4 و U0=0.4 ورسم الحل u مقابل t ∈ [0,1] ، فيمكنك القيام بما يلي
t = np.linspace(0, 1)lmd = 4 * np.ones_like(t)u0 = 0.4 * np.ones_like(t)u = محلول (t, lmd, u0, to_numpy=True) استيراد matplotlib.pyplot كـ pltplt .مؤامرة (ر، ش)
بمجرد حصولك على solution مجمع، يمكنك العثور على مجموعة من المعلمات (λ, U0) التي تطابق نقاط البيانات المرصودة (t_i, u_i) بشكل وثيق. يتم تحقيق ذلك باستخدام نزول متدرج بسيط. في مثال اللعبة التالي، نفترض أن هناك ثلاث نقاط بيانات فقط u(0.2) = 0.273 و u(0.5)=0.129 و u(0.8) = 0.0609 . فيما يلي سير عمل PyTorch الكلاسيكي.
# نقاط البيانات المرصودة = torch.tensor([0.2, 0.5, 0.8]).reshape(-1, 1)u_obs = torch.tensor([0.273, 0.129, 0.0609]).reshape(-1, 1)# التهيئة العشوائية من α وU0؛ تتبع تدرجهاlmd_tensor = torch.rand(1) * (LAMBDA_MAX - LAMBDA_MIN) + LAMBDA_MINu0_tensor = torch.rand(1) * (U0_MAX - U0_MIN) + U0_MINadam = torch.optim.Adam([lmd_tensor.requires_grad_(True)، u0_tensor.requires_grad_(True)], lr=1e-2)# تشغيل نزول متدرج لمدة 10000 حقبةfor _ in range(10000):output =solution(t_obs, lmd_tensor * torch.ones_like(t_obs), u0_tensor * torch.ones_like(t_obs ))الخسارة = ((الإخراج - u_obs) ** 2).mean()loss.backward()adam.step()adam.zero_grad()
طباعة (f"μ = {lmd_tensor.item()}, U0={u0_tensor.item()}, الخسارة = {loss.item()}") بسيط. عند استيراد neurodiffeq، تكتشف المكتبة تلقائيًا ما إذا كان CUDA متاحًا على جهازك. نظرًا لأن المكتبة تعتمد على PyTorch، فسوف تقوم بتعيين نوع الموتر الافتراضي على torch.cuda.DoubleTensor في حالة العثور على جهاز GPU متوافق.
راجع أقسام الشبكات المخصصة ونقل التعلم.
طريقة PyTorch القياسية.
قم ببناء شبكاتك كما هو موضح في الشبكات المخصصة: nets = [FCNN(), FCN(), ...]
قم بإنشاء مثيل لمُحسِّن مخصص وتمرير جميع معلمات هذه الشبكات إليه
بارامترات = [p for net in nets for p in net.parameters()] # قائمة معلمات جميع الشبكاتMY_LEARNING_RATE = 5e-3optimizer = torch.optim.Adam(parameters, lr=MY_LEARNING_RATE, ...)
قم بتمرير كل من nets optimizer إلى الحل: solver = Solver1D(..., nets=nets, optimizer=optimizer)
على عكس الطرق الرقمية التقليدية (FEM، FVM، وما إلى ذلك)، يتطلب الحل القائم على NN بعض الضبط المفرط. توفر المكتبة أقصى قدر من المرونة لتجربة أي مجموعة من المعلمات الفائقة.
لاستخدام بنية شبكة مختلفة، يمكنك تمرير torch.nn.Module s المخصص الخاص بك.
لاستخدام مُحسِّن مختلف، يمكنك تمرير المُحسِّن الخاص بك إلى solver = Solver(..., optimizer=my_optim) .
لاستخدام توزيع عينات مختلف، يمكنك استخدام المولدات المضمنة أو كتابة المولدات الخاصة بك من البداية.
لاستخدام حجم عينة مختلف، يمكنك تعديل المولدات أو تغيير solver = Solver(..., n_batches_train) .
لتغيير المعلمات الفائقة ديناميكيًا أثناء التدريب، تحقق من ميزة عمليات الاسترجاعات الخاصة بنا.
لا تستخدم ReLU للتنشيط، لأن مشتقه من الدرجة الثانية يساوي 0.
قم بإعادة قياس PDE/ODE الخاص بك في شكل بلا أبعاد، ويفضل جعل كل شيء يتراوح بين [0,1] . العمل مع مجال مثل [0,1000000] عرضة للفشل لأن أ) يقوم PyTorch بتهيئة أوزان الوحدات لتكون صغيرة نسبيًا و ب) معظم وظائف التنشيط (مثل Sigmoid وTanh وSwish) تكون غير خطية بالقرب من 0.
إذا كان PDE/ODE الخاص بك معقدًا للغاية، ففكر في تجربة تعلم المناهج الدراسية. ابدأ بتدريب شبكاتك على نطاق أصغر، ثم قم بالتوسع تدريجيًا حتى يتم تغطية النطاق بالكامل.
الجميع مدعوون للمساهمة في هذا المشروع.
عند المساهمة في هذا المستودع، نأخذ في الاعتبار العملية التالية:
افتح موضوعًا لمناقشة التغيير الذي تخطط لإجرائه.
انتقل من خلال إرشادات المساهمة.
قم بإجراء التغيير على مستودع متشعب وقم بتحديث README.md إذا تم إجراء تغييرات على الواجهة.
افتح طلب السحب.