Rubik's Cube Solver للمكعبات الكبيرة جدًا.
يحل أي مكعب من أي حجم من 1 إلى 65536. يمكن تعديل الكود بسهولة للتعامل مع مكعبات أكبر. ومع ذلك ، فإن القيد الأساسي هو مقدار الذاكرة على النظام وطول المدة التي يستغرقها حلها. حل الوقت ينمو ~ n^2 وهذا يعني أن الأمر يستغرق 4-5 مرات لفترة أطول لحل المكعب الذي يكون أكبر 2x في كل بعد.
يمكن حل مكعب 1024 طبقة في حوالي 1.5 ثانية. يمكن حل مكعب 16384 طبقة في حوالي 20 دقيقة.
يوتيوب: حل 65536 طبقات يوتيوب: حل 32768 طبقات
صورة الوجه الأمامي لمكعب 32768
يحل المراكز ثم الزوايا ثم الحواف
يتم حل المراكز في 15 مرحلة حيث تحرك كل مرحلة جميع قطع لون معين من وجه واحد إلى الوجه المطلوب. على سبيل المثال: تحرك المرحلة جميع القطع الخضراء على الوجه الأبيض إلى الوجه الأخضر. كرر هذا لجميع الألوان والوجوه.
يستخدم Solver المتسابق الموصوف هنا والذي يمكنه تنقل القطع المركزية من رباعي من الوجه إلى مأزق على وجه آخر. خاصية مهمة للغاية لهذا المتنقل هي أنه يمكن تعديلها لتحريك العديد من القطع في صف واحد في نفس الوقت. For very large cubes this means it can move hundreds if not thousands of pieces in a single operation. The average number of moves k = (2 * P + 5) / P where P is the number of pieces that can be moved per operation. K quickly approaches 2 as the cube size increases.
The corners are solved using a basic brute force method of moving the corner into place and then rotating until the faces were oriented correctly. Will Smith يمكن أن يشرح: https://www.youtube.com/watch؟v=WBZKDRC9VQS
يتم حل الحواف عن طريق تحريك كل زوج من الحواف إلى الوجه الأمامي ، ثم تبديل القطع المطلوبة من الحافة اليسرى إلى الحافة اليمنى. عدد من الوظائف عند الحاجة لإصلاح أو منع مشاكل التكافؤ.
دورات الوجه مجانية بشكل أساسي. Instead of moving all the pieces on a given face (N^2 pieces) to perform a rotation, the solver simply changes the coordinate system that is uses to read/write to the face. هذا يحفظ كمية هائلة من تبديل البيانات.
// Virtually rotate this face by q * 90 degrees
inline void Face::RotatefaceCW ( const int q)
{
orientation = (orientation + q) & 3 ;
}
// Gets the value of this face at coordinates r = row, c = column
inline const byte Face::GetRC ( const uint r, const uint c) const
{
switch (orientation) {
case 0 :
return data[(r << BS) + c];
case 1 :
return data[(c << BS) + (R1 - r)];
case 2 :
return data[((R1 - r) << BS) + (R1 - c)];
case 3 :
return data[((R1 - c) << BS) + r];
default :
return 0 ;
}
}يتضمن هذا الرمز مصدرًا بسيطًا للصور يتم استخدامه يجعل كل وجه في صورة.
https://www.nayuki.io/page/tiny-png-utput
https://github.com/nayuki/Nayuki-web-published-code
Tiny PNG Output هي مكتبة مستقلة صغيرة ، متوفرة في C و C ++ ، والتي تأخذ RGB8.8.8 بكسل وتكتب ملف PNG.
يمكن تقدير إجمالي عدد الحركات باستخدام صيغة بسيطة. Assuming the cube is sufficiently randomized, we can expect the first face to be 1/6 solved and therefore 5/6 of the pieces will have to be moved. سيتم حل الوجه الثاني 1/5 ويتطلب نقل 4/5 من القطع. الوجه الثالث 3/4 ، الوجه الرابع 2/3 ، الوجه الخامس 1/2 وسيتم حل الوجه الأخير بالكامل. يمكن تقدير متوسط عدد الحركات (K) لتحريك قطعة واحدة تجريبياً على أنه ~ 2.1. تنخفض قيمة K مع زيادة حجم المكعب. لا يمكن أن تكون القيمة أقل من 2 لأن المتسابق يتطلب نقل كل قطعة مرتين على الأقل.
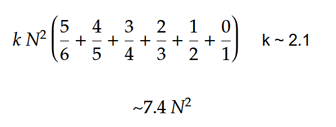
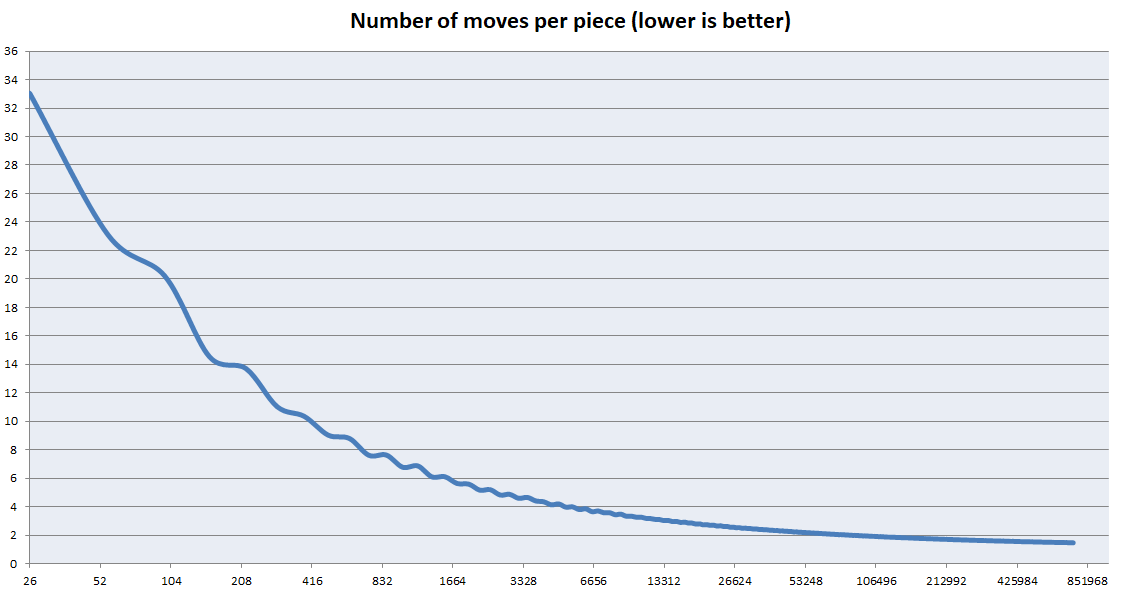
تم تحسين هذه الخوارزمية للمكعبات الكبيرة جدًا. ومع ذلك فهو فظيع للمكعبات الصغيرة. ركزت التحسينات الأولية على حل المراكز في أسرع وقت ممكن ولم يتم إعطاء أي اعتبار لحل الحواف. ومع ذلك ، فإن حجم الحواف ضئيلة مقارنة بالمراكز مع زيادة حجم المكعب. يوضح الرسم البياني أدناه كيف يتناقص متوسط عدد الحركات لكل قطعة مع مكعبات أكبر. ملاحظة: هذا ليس رسم بياني لـ K. إنه رسم بياني لـ (إجمالي الحركات) / (عدد القطع)
cmake -B build -S .
cd build
cmake --build .
RCube/RCube