autodiff

Autodiff - مكتبة التمايز التلقائي C ++

انتقل هذا المشروع إلى BOOST (الرياضيات/التمايز/AUTODIFF) ولم يعد هذا المستودع يتم تحديثه.

بناء الحالة

فرع	ترافيس	Appveyor	Codecov.io
master
develop

وصف

Autodiff هي مكتبة C ++ رأس فقط تسهل التمايز التلقائي (الوضع الأمامي) للوظائف الرياضية للمتغيرات المفردة والمتعددة.

يعتمد هذا التنفيذ على توسيع سلسلة Taylor لوظيفة تحليلية F عند النقطة X₀ :

الفكرة الأساسية لـ Autodiff هي استبدال الأرقام ذات الحدود الحية في تقييم F (X₀) . عن طريق استبدال الرقم X₀ مع الحدود الحدود من الدرجة الأولى ، X₀+ε ، واستخدام نفس الخوارزمية لحساب F (X₀+ε) ، فإن متعدد الحدود الناتج في ε يحتوي على مشتقات الوظيفة F '(x₀) ، f' (x₀) و F '' '(x₀) ، ... داخل المعاملات. كل معامل يساوي مشتق ترتيب كل منهما ، مقسومًا على عازف النظام.

بمزيد من التفصيل ، افترض أن المرء مهتم بحساب المشتقات الأولى من F في X₀ . بدون فقدان الدقة في حساب المشتقات ، يمكن التخلص من جميع المصطلحات O (ε ⁿ⁺¹ ) التي تشمل صلاحيات ε أكبر من n . (ويرجع ذلك إلى حقيقة أن كل مصطلح في كثير الحدود يعتمد فقط على مصطلحات متساوية ومنخفضة تحت العمليات الحسابية )

تتيح قدرة C ++ على الحمل الزائد للمشغلين والوظائف إنشاء فئة fvar التي تمثل متعدد الحدود في ε . وبالتالي ، يتم استخدام نفس الخوارزمية f التي تحسب القيمة الرقمية لـ y₀ = f (x₀) ، عند كتابتها لقبول وإرجاع متغيرات نوع عام (قالب) ، لحساب متعدد الحدود ʃ _n y _n εⁿ = f (x₀+ ε) . ثم يتم العثور على المشتقات f ⁽ⁿ⁾ (x₀) من ناتج العامل المعني n! ومعامل y _n :

مثال 1: تمايز متغير واحد

 #include <boost/math/intariation/autodiff.hpp> #include <IoStream> template <typename t>
T Fourth_Power (t const & x) {
  t x4 = x * x ؛  // Retval in Operator*() يستخدم ذاكرة X4 عبر NRVO.
  x4 *= x4 ؛      // لا توجد نسخ من X4 داخل المشغل*= () حتى عند التربيع.
  إرجاع x4 ؛     // x4 يستخدم ذاكرة y في main () عبر nrvo.} int main () {باستخدام مساحة الاسم Boost :: Math :: التمايز ؛

  Constexpr غير موقعة = 5 ؛                  // أعلى مشتق من الطلب ليتم حسابه.
  Auto const x = make_fvar <double ، order> (2.0) ؛  // ابحث عن المشتقات في x = 2.
  Auto const y = fourth_power (x) ؛  ل (غير موقعة i = 0 ؛ i <= order ؛ ++ i)
    std :: cout << "y.derivative (" << i << ") =" << y.derivative (i) << std :: endl ؛  العودة 0 ؛
}/*الإخراج: y.derivative (0) = 16y.

ما سبق يحسب

مثال 2: تمايز متعدد المتغيرات ومتعدد الدقة

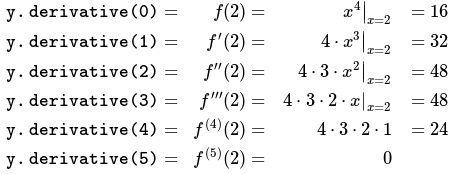
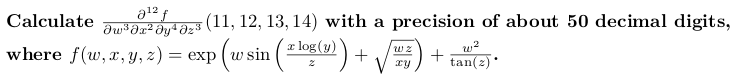
 #include <boost/math/intariation/autodiff.hpp> #include <boost/multiprecision/cpp_bin_float.hpp> #include <IoStream> باستخدام مساحة الاسم: typename z>
PROMOTE <W ، X ، Y ، Z> F (const w & w ، const x & x ، const y & y ، const z & z) {باستخدام مساحة الاسم std ؛
  إرجاع exp (w * sin (x * log (y) / z) + sqrt (w * z / (x * y))) + w * w / tan (z) ؛
} int main () {باستخدام float50 = boost :: multiprecision :: cpp_bin_float_50 ؛  constexpr غير موقعة NW = 3 ؛  // Max Order of Derivative to Wexulate for w
  constexpr غير موقعة nx = 2 ؛  // الحد الأقصى للترتيب المشتق لحساب x
  constexpr غير موقعة NY = 4 ؛  // الحد الأقصى للترتيب المشتق لحساب y
  constexpr غير موقعة NZ = 3 ؛  // الحد الأقصى للترتيب المشتق لحساب ل z
  // إعلان 4 متغيرات مستقلة معًا في std :: tuple.
  متغيرات const Auto = make_ftuple <float50 ، NW ، NX ، NY ، NZ> (11 ، 12 ، 13 ، 14) ؛  Auto const & w = std :: get <0> (المتغيرات) ؛  // تصل إلى مشتقات NW في W = 11
  Auto const & x = std :: get <1> (المتغيرات) ؛  // حتى مشتقات NX عند x = 12
  Auto const & y = std :: get <2> (المتغيرات) ؛  // حتى مشتقات نيويورك في y = 13
  Auto const & z = std :: get <3> (المتغيرات) ؛  // حتى مشتقات NZ عند z = 14
  Auto const v = f (w ، x ، y ، z) ؛  // محسوبة من التمايز الرمزي الرياضي.
  Float50 Const Assfer ("1976.31960074777777779881875290418720908121189218755") ؛
  std :: cout << std :: setPrecision (std :: numeric_limits <loat50> :: digits10)
            << "Mathematica:" << الإجابة << 'n' << "autodiff:" << v.derivative (NW ، NX ، NY ، NZ) << 'n' << std :: setPrecision (3)
            << "خطأ نسبي:" << (v.derivative (NW ، NX ، NY ، NZ) / Assember - 1) << 'n' ؛  العودة 0 ؛
}/*الإخراج: Mathematica: 1976.319600747777177798818752904187209081211892188AUTODIFF: 1976.3196007477977177779818752904187209081212121212121212121218921892189218921892189218921892189218921.

مثال 3: تسعير خيار Black-Scholes مع الإغريق تلقائيًا

 #include <boost/math/intariation/autodiff.hpp> #include <IoStream> باستخدام مساحة الاسم: https://en.wikipedia.org/wiki/greeks_(finance)#formulas_for_european_option_greeks// Standard Normal Trendative Distribution FunctionTemplate <typename x>
x phi (x const & x) {return 0.5 * erfc (-one_div_root_two <x> () * x) ؛
} enum class cp {call ، put} ؛ // افترض صفر عائد الأرباح السنوية (q = 0).
تعزيز <السعر ، Sigma ، Tau ، معدل> Black_Scholes_Option_Price (CP CP ، Double K ،
                                                            السعر const & s ،
                                                            Sigma const & sigma ،
                                                            تاو كونست وتاو ،
                                                            معدل const & r) {باستخدام مساحة الاسم std ؛
  Auto const d1 = (log (s / k) + (r + sigma * sigma / 2) * tau) / (sigma * sqrt (tau)) ؛  Auto const d2 = (log (s / k) + (r - sigma * sigma / 2) * tau) / (sigma * sqrt (tau)) ؛  Switch (cp) {case cp :: call: return s * phi (d1)-exp (-r * tau) * k * phi (d2) ؛ case cp :: put: return exp (-r * tau) * k * phi (-d2)-s * phi (-d1) ؛
  }
} int main () {double const k = 100.0 ؛                    // سعر الإضراب.
  Auto const s = make_fvar <double ، 2> (105) ؛  // سعر السهم.
  const double sigma = 5 ؛                    // التقلب.
  const double tau = 30.0 / 365 ؛             // حان الوقت لانتهاء الصلاحية في سنوات. (30 يومًا).
  const double r = 1.25 / 100 ؛               // سعر الفائدة.
  Auto const call_price = black_scholes_option_price (cp :: call ، k ، s ، sigma ، tau ، r) ؛  Auto const put_price = black_scholes_option_price (cp :: put ، k ، s ، sigma ، tau ، r) ؛

  std :: cout << <<< .  العودة 0 ؛
}/*الإخراج: سعر الاتصال الأسود السوداء = 56.5136Black-scholes وضع السعر = 51.4109CALL DELTA = 0.773818PUT DELTA = -0.226182CALL GAMMA = 0.00199852PUT GAMMA = 0.00199852*/

انظر مثال/Black_scholes.cpp للحصول على قائمة أكبر من اليونانيين المحسوسين تلقائيًا.

مزايا التمايز التلقائي

توضح الأمثلة المذكورة أعلاه بعض مزايا استخدام Autodiff:

• التخلص من التكرار رمز. إن وجود وظائف منفصلة لحساب المشتقات هو شكل من أشكال التكرار الكود ، مع جميع الالتزامات التي تأتي معها:

• تتطلب التغييرات على وظيفة واحدة تغييرات إضافية على وظائف أخرى. في المثال الثالث أعلاه ، ضع في اعتبارك أكبر حجم الكود المذكور أعلاه وبين المعتاد في حالة كتابة وظيفة منفصلة لكل قيمة يونانية.

• التبعيات على وظيفة مشتقة لغرض مختلف سوف تنكسر عند إجراء التغييرات على الوظيفة الأصلية. ما لا يحتاج إلى الوجود لا يمكن أن يكسر.

• رمز الانتفاخ ، تقليل النزاهة المفاهيمية. يكون التحكم في تطور الكود أسهل/أكثر أمانًا عندما تكون قاعدة التعليمات البرمجية أصغر وقادرة على إمساكها بشكل حدسي.

• دقة المشتقات على أساليب الاختلاف المحدودة. تتضمن أساليب الاختلاف المحدودة أحادية التهدئة دائمًا متغيرًا خاليًا من Δx يجب اختياره بعناية لكل تطبيق. إذا كانت Δx صغيرة جدًا ، فإن الأخطاء العددية تصبح كبيرة. إذا كانت Δx كبيرة جدًا ، فإن الأخطاء الرياضية تصبح كبيرة. مع Autodiff ، لا توجد متغيرات مجانية لضبطها ودقة الإجابة بشكل عام متفوق على طرق الفرق المحدودة حتى مع أفضل خيار Δx .

يدوي

التفاصيل الإضافية في دليل Autodiff.

رخصة

تم توزيعه تحت ترخيص برنامج Boost ، الإصدار 1.0.

ملكيات

• رأس فقط.

• مُحسّن لـ C ++ 17. يقوم أيضًا بتجميع واختبار مع معايير C ++ 11 و C ++ 14 ومعايير C ++ 20 المقترحة.

• يتم تخصيص جميع الذاكرة على المكدس.

الدلائل

اسم	غاية
doc	الوثائق
example	أمثلة
include	الرؤوس
test	اختبارات الوحدة

مزيد من المعلومات

• الأخطاء التقارير: تأكد من ذكر إصدار Boost و Platform و Reloper الذي تستخدمه. عينة رمز صغيرة قابلة للتجميع لإعادة إنتاج المشكلة جيدة دائمًا أيضًا.

• أرسل تصحيحاتك كطلبات سحب مقابل فرع التطوير. لاحظ أنه من خلال تقديم تصحيحات ، فإنك توافق على ترخيص التعديلات الخاصة بك بموجب ترخيص برنامج Boost ، الإصدار 1.0.