
ومهام Fiber في React، ومهام Fiber المختلفة لها أولويات مختلفة، وتحتاج React إلى معالجة المهام ذات الأولوية العالية أولاً. على سبيل المثال، تعد نقرات المستخدم ومدخلاته مهام ذات أولوية عالية، لأن عمليات المستخدم تأمل بالتأكيد أن يكون لها تأثيرات فورية، وذلك لتحسين تجربة المستخدم. على سبيل المثال، يجب أن تكون أولوية أحداث الرسوم المتحركة أقل. بعد أن تدخل مهمة جديدة ذات أولوية عالية إلى قائمة الانتظار، تحتاج React إلى معالجتها أولاً.
لتخزين هذه المهام، يوجد مجموعتي مهام في React.
// يتم تخزين المهام في كومة صغيرة var TaskQueue = []; var timerQueue = []
;
فار مهمة جديدة = {
المعرف: TaskIdCounter++، // تحديد معرف المهمة
رد الاتصال، // مستوى أولوية وظيفة رد الاتصال، // وقت بداية المهمة، // وقت بدء المهمة، وقت انتهاء الصلاحية، // وقت انتهاء الصلاحية، نقطة زمنية، مؤشر الترتيب: -1، // فرز المهام، تأتي القيمة من وقت انتهاء الصلاحية، لذا القيمة كلما كانت القيمة أصغر، زادت الأولوية}؛ بمجرد وصول مهمة جديدة إلى React، ستستخدم أولًا الوقت الحالي لتسجيل الوقت الحالي (performance.now() أو Date.now()). معلمة التأخير، ثم تبدأ المهمة في وقت التنفيذ startTime = currentTime + Delay;. بعد ذلك، إذا تم إنشاء startTime >currentTime، فهذا يثبت أنه يمكن تأجيل المهمة، ثم تدخل المهمة في قائمة انتظار الوقت، وإلا فإنها تدخل في قائمة انتظار المهام.
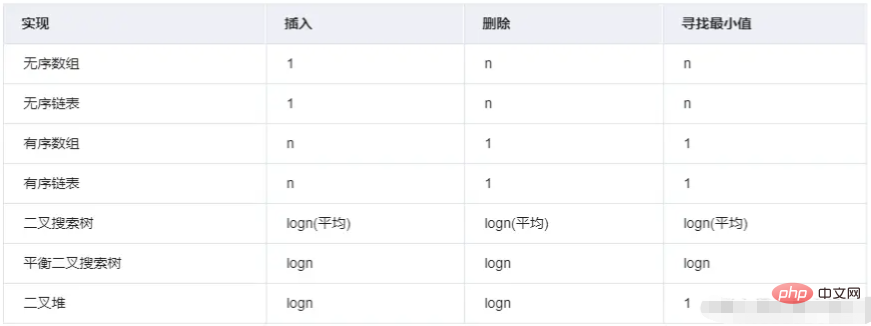
كيف تعثر React على المهمة ذات الأولوية القصوى؟ لنأخذ TaskQueue كمثال، وهو عبارة عن تجمع مهام ديناميكي (قائمة انتظار المهام)، ونموذج البيانات عبارة عن مصفوفة. بالطبع، يمكنك الفرز حسب الأولوية، أي Array.sort. عند إضافة مهمة جديدة إلى قائمة الانتظار، يتم فرزها أولاً، ثم يتم العثور على المهمة ذات الأولوية القصوى وتنفيذها. لكن متوسط التعقيد الزمني لـ Array.sort هو O(nlogn)، وهو ليس الحل الأفضل.
يتم استخدام SortIndex للفرز في newTask الخاص بـ TaskQueue. يتم أخذ هذه القيمة من وقت انتهاء الصلاحية، مما يعني أنه كلما زادت المهمة ذات الأولوية، زادت الحاجة إلى فهمها وتنفيذها، وبالتالي فإن وقت انتهاء الصلاحية سيكون أصغر كلما زادت الأولوية، كلما كان وقت انتهاء الصلاحية أصغر، كلما كان مؤشر الفرز أصغر بشكل طبيعي. في الواقع، هذه هي قائمة الانتظار ذات الأولوية .
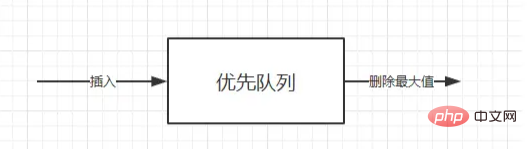
هي أيضًا نوع من قوائم الانتظار ( أولاً وقبل كل شيء، هي قائمة انتظار، وثانيًا، ذيل للداخل، أولًا للخارج ). والفرق الوحيد هو أن ترتيب قائمة الانتظار لقائمة الانتظار ذات الأولوية يعتمد على الأولوية في بعض الحالات ، قد تحتاج إلى العثور على الحد الأدنى أو الحد الأقصى للعنصر في مجموعة العناصر التي يمكن تشغيلها باستخدام قائمة انتظار الأولوية ADT قائمة انتظار الأولوية ADT عبارة عن بنية بيانات تدعم عمليات إدراج وحذف الحد الأدنى من القيمة (إرجاع وحذف العنصر الأدنى) أو حذف عملية القيمة القصوى (إرجاع وحذف العنصر الأدنى وإزالة العنصر الأكبر).
إذا كان العنصر ذو أصغر قيمة مفتاح له الأولوية العليا، فإن قائمة انتظار الأولوية هذه تسمى قائمة انتظار ذات أولوية تصاعدية (أي، يتم دائمًا حذف العنصر الأصغر أولاً). وبالمثل، إذا كان العنصر ذو أكبر قيمة رئيسية له الأولوية القصوى، فإن هذا النوع من قائمة انتظار الأولوية يسمى قائمة انتظار الأولوية التنازلية (أي يتم حذف العنصر الأكبر دائمًا أولاً)؛ نظرًا لأن هذين النوعين متماثلان، فأنت بحاجة فقط إلى ذلك للتركيز على واحد منهم، مثل قائمة الانتظار ذات الأولوية التصاعدية.
على سبيل المثال : عندما كنا نشتري التذاكر، كنا جميعًا نقف في الطابور وكانت لدينا نفس الأولوية. ومن كان في الصف كان يشتري التذكرة أولاً، ولكن بعد ذلك جاء جندي وكان لديه أولوية أعلى وكان في الطابور مباشرة الجبهة.
يتم استخدام الحد الأدنى من الكومة (كومة جذر صغيرة، كومة علوية صغيرة...) في React لتحقيق هذه الوظيفة. وذلك لتحويل قائمة المهام إلى الحد الأدنى من الكومة، ثم إخراج المهمة العليا للتنفيذ، وتكديس قائمة المهام، والاحتفاظ بها كحد أدنى من بنية بيانات الكومة. عند إدراج مهمة جديدة في قائمة المهام، يجب أيضًا تكديسها والاحتفاظ بها دائمًا كحد أدنى من الكومة.
: في بعض الأماكن، تسمى الكومة بقائمة الانتظار ذات الأولوية (غير دقيقة)، فهي في المقام الأول قائمة انتظار ولها خصائص قائمة الانتظار، أي " الوارد أولاً يخرج أولاً ". . ثانيًا، العناصر الموجودة في قائمة الانتظار هذه لها أولويات، وسيتم تصنيف العناصر ذات الأولويات الأعلى في المرتبة الأولى.
على وجه الدقة، الكومة هي وسيلة لتنفيذ قائمة انتظار ذات أولوية. بالطبع، يمكن أيضًا تنفيذ قوائم الانتظار ذات الأولوية بطرق أخرى.
قلنا من قبل أن فرز الكومة هو فرز غير مستقر، ولكن تأمل TaskQueue أن تكون هذه العملية مستقرة، وهذا يعني أنه إذا كان من الممكن أن يكون وقت انتهاء مهمتين هو نفسه، فإن ذلك يعتمد على من يدخل. أولاً، مجمع المهام هو قيمة معرف newTask. في كل مرة تأتي مهمة جديدة، سيتم زيادة المعرف بمقدار 1.
مقارنة الدالة (أ، ب) {
// قارن فهرس الفرز أولاً، ثم معرف المهمة.
const diff = a.sortIndex - b.sortIndex;
إرجاع الفرق !== 0 ؟
} قبل فهم الحد الأدنى من الكومة، دعونا نراجع المعرفة الأساسية.
تشيرإلى شجرة مرتبة لا تزيد فيها درجة العقد في الشجرة عن 2. وهي أبسط شجرة وأكثرها أهمية.
هي شجرة ثنائية تحتوي فيها جميع العقد على كل مستوى على عقدتين فرعيتين، باستثناء المستوى الأخير الذي لا يحتوي على أي عقد فرعية.
من منظور رسومي، تبدو الشجرة الثنائية الكاملة وكأنها مثلث.
إذا كان عدد مستويات الشجرة الثنائية هو K والعدد الإجمالي للعقد هو (2^k) -1، فهي شجرة ثنائية كاملة.
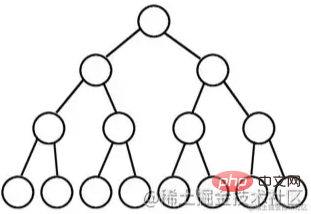
الشجرة الثنائية الكاملة تعني "البنات لها كلا الجانبين" وهي مثالية جدًا، لذلك تسمى شجرة ثنائية كاملة.
باستثناء العقد الورقية، تكون درجة جميع العقد 2. بمعنى آخر، يمكن أن تكون درجة جميع العقد 0 أو 2 فقط.
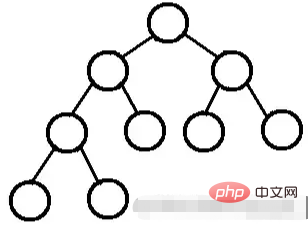
الشجرة الثنائية المثالية ليس لها أطفال أو كلاهما.
النص الإنجليزي الأصلي للشجرة الثنائية الكاملة:
الشجرة الثنائية الكاملة (FBT) هي شجرة تحتوي كل عقدة فيها بخلاف الأوراق على طفلين.
النص الإنجليزي الأصلي للشجرة الثنائية المثالية:
الشجرة الثنائية المثالية (PBT) هي شجرة بها جميع العقد الورقية على نفس العمق
.جميع العقد الداخلية لها الدرجة 2.
تشير جميع الكتب الأجنبية إلى أقدم الكتب المدرسية المترجمة حول الأشجار الثنائية الكاملة والأشجار الثنائية المثالية، لكن المقالات المترجمة الأقدم تمت ترجمتها بشكل خاطئ. الآن في الصين، لا يمكننا أن نرتكب الأخطاء إلا عندما نكون مخطئين (الجميع مخطئون، ومن ثم فإن المخطئ هو أيضًا على حق. على سبيل المثال، جماعات الضغط...). إذا كنت تريد مناقشة هذين المفهومين مع أصدقاء أجانب، فعليك أن تنتبه.
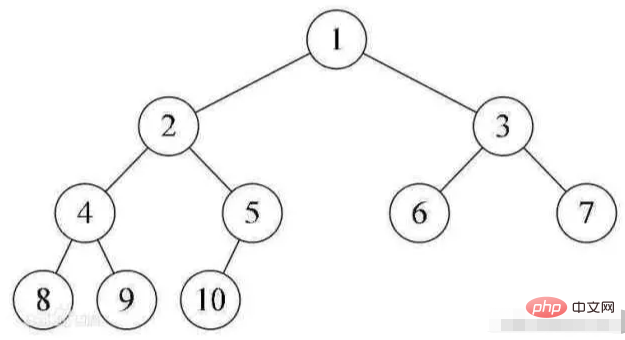
الشجرة الثنائية(CBT) هي شجرة ثنائية يتم فيها ملء كل مستوى، باستثناء المستوى الأخير، بالكامل، وتكون جميع العقد في أقصى اليسار قدر
الإمكان الشجرة من الأعلى إلى الأسفل ومن اليسار إلى اليمين إذا كانت العقدة المرقمة i (1≥i≥n) موجودة في الشجرة الثنائية مع العقدة المرقمة i في الشجرة الثنائية الكاملة، إذا كانت المواضع متماثلة، فستكون الشجرة الثنائية كذلك. تسمى شجرة ثنائية كاملة.
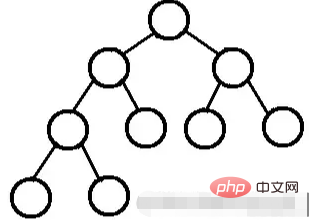
تفي الكومة دائمًا بالخصائص التالية:
ويجب علينا أولاً فهم الكومة الجذرية الكبيرة كومة الجذر الصغيرة في الشجرة الثنائية الكاملة تكون جميع العقد أكبر (أو أصغر) من العقد التابعة لها، لذلك هناك حالتان هنا، الحد الأقصى للكومة والحد الأدنى من الكومة.
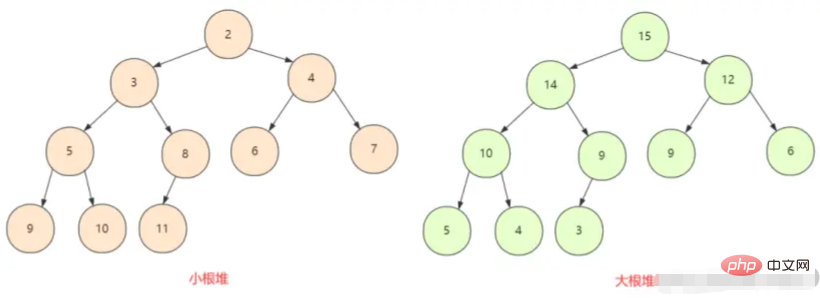
عادةً ما تكون الكومة عبارة عن مجموعة من الكائنات التي يمكن عرضها على أنها شجرة ثنائية كاملة . بالطبع، يمكن أيضًا تمثيل الأشجار الثنائية بواسطة المصفوفات.
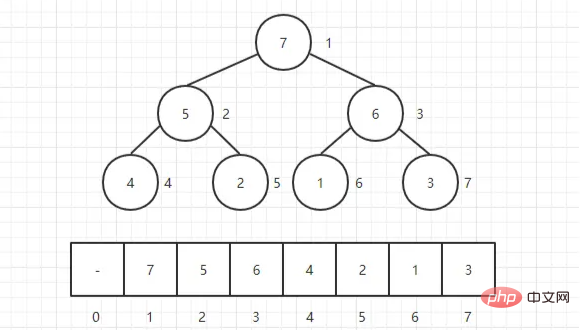
هي بناء الكومة أولاً ثم تعديلها.
، لشجرة ثنائية (تمثيل مصفوفة)، نقوم بالتعديل من الأسفل إلى الأعلى، بدءًا من "العقدة غير الورقية الأولى" ثم التعديل للأمام. قواعد التعديل هي كما يلي:
بناء الكومة هو O(n ) عملية تعقيد الوقت.
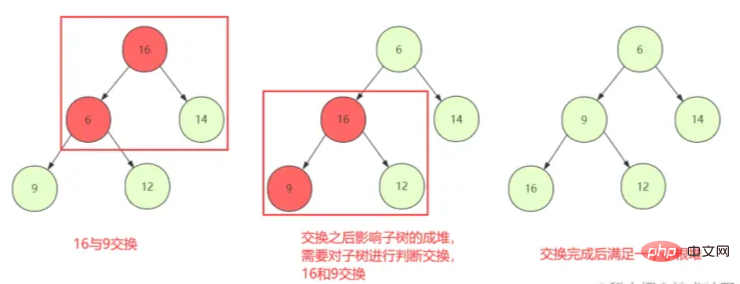
① ابدأ من العقدة غير الورقية الأولى للحكم على المبادلة لأسفل (ShiftDown)، بحيث يمكن للعقدة الحالية والفرعية الحفاظ على خصائص الكومة
② ومع ذلك، قد لا يكون استبدال العقدة العادية مشكلة إذا كسر التبادل خصائص بنية الكومة للطفل، فيجب إعادة ShiftDown للعقدة التي تم تبديلها حتى تتوقف.
الكومة
إلى تدمير بنية الكومة.
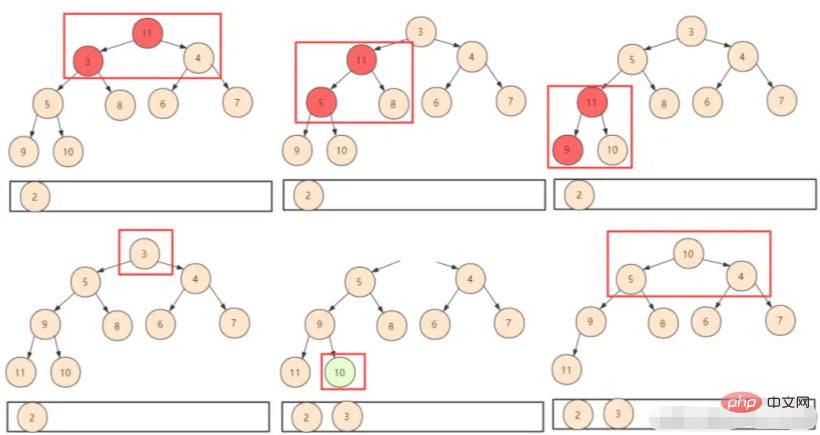
① لذا، ضع العنصر الأخير أولاً. بهذه الطريقة، ما عليك سوى الحكم على إزاحة المبادلة (shiftDown)، ولكن عليك ملاحظة أن حجم الكومة بأكملها قد تغير في هذا الوقت، ولن نستخدم الموضع المهمل بشكل منطقي، لذلك نحتاج إلى تضمين الكومة معلمة الحجم عند تصميم الوظيفة.
② كرر العملية المذكورة أعلاه حتى يتم الحصول على جميع العناصر الموجودة في الكومة.
من حيث تحليل تعقيد خوارزمية الكومة، كان التعقيد الزمني السابق لبناء الكومة هو O(n). في كل مرة يتم حذف الجزء العلوي من الكومة ثم تبديلها للأسفل، يتم تسجيل رقم كل منها. بهذه الطريقة، التعقيد هو O(nlogn)، والتعقيد الزمني الإجمالي هو O(n)+O(nlogn)=O(nlogn).
Heap مناسبة للحفاظ على الحد الأقصى لقيمة المجموعة.
بعد إخراج العنصر من الكومة، تكون تكلفة إعادة الضبط للحصول على العنصر العلوي من الكومة (أي ثاني أعلى قيمة) منخفضة نسبيًا، لأنه بعد إخراج العنصر، تكون الكومة شبه - المنتج النهائي، ويتم الحصول على ثاني أعلى قيمة من منتج شبه نهائي، بالطبع التكلفة منخفضة نسبيًا، والتعقيد الزمني هو O(logn)، ولكن إذا تم اجتيازه مرة واحدة للعثور على ثاني أعلى قيمة، التعقيد الزمني هو O(n).
كودمكتوب بلغة Javascript ES6.
كومة فئة{
منشئ (البيانات، شركات) {
this.data = البيانات ? البيانات : [];
// قواعد المقارنة: أكثر مرونة، يمكنك مقارنة القيم أو الكائنات this.compartor = comp ?
// الضبط على الكومة (قائمة الانتظار ذات الأولوية)
this.heapify();
}
هيابيفي () {
if(this.size() <= 1) return;
// ابدأ الضبط من العقدة غير الورقية الأولى، أو يمكنك الضبط من العنصر الأخير for(let i=Math.floor((this.size()-2)/2); i>=0; i-- ) {
// ضبط الكومة. يمكن أيضًا تنفيذ الضبط التنازلي باستخدام التكرار هنا، ويتم استخدام التكرار لتنفيذ this.shiftDown(i);
}
}
// ضبط التحول للأسفل (i) {
دع اليسار = 2*i +1;
دع اليمين = 2*i +2;
دع لين = this.size();
بينما (أنا <لين) {
Let findIndex = i;
// الطفل الأيسر "أكبر"
إذا (left < len && this.compartor(this.data[left], this.data[findIndex]) < 0) {
findIndex = left;
}
// الطفل المناسب "أكبر"
إذا (يمين < لين && this.compartor(this.data[right], this.data[findIndex]) < 0) {
findIndex = right;
}
إذا (أنا !== تجد الفهرس) {
// استبدل العقدة الحالية بقيمة أكبر [this.data[i], this.data[findIndex]] = [this.data[findIndex], this.data[i]];
// بعد ضبط هذه الطبقة، قد يؤثر ذلك على خصائص كومة الطبقة السفلية، لذا استمر في ضبط الطبقة السفلية (التنفيذ التكراري، أو العودي)
i = findIndex;
اليسار = 2*i +1;
يمين = 2*i +2;
}
آخر {
// إذا لم تكن هناك حاجة إلى أي تعديل، فاقفز للخارج (يجب القفز للخارج، وإلا فلن تنتهي الحلقة)
استراحة؛
}
}
}
// ضبط التحول التصاعدي (ط) {
// ابحث عن رمز الأصل LetparentIndex = Math.floor((i-1)/2);
// اضبط الحد الأقصى على 0
بينما (parentIndex >=0 ) {
Let findIndex = i;
إذا (this.compartor(this.data[parentIndex], this.data[findIndex]) > 0) {
findIndex =parentIndex;
}
إذا (findIndex !== ط) {
[this.data[i], this.data[findIndex]] = [this.data[findIndex], this.data[i]];
i = findIndex;
parentIndex = Math.floor((i-1)/2);
}
آخر {
استراحة؛
}
}
}
// احصل على عدد جميع العناصر الموجودة في الكومة size(){
إرجاع this.data.length;
}
// احصل على العنصر الأول من نظرة خاطفة على الكومة(){
if(!this.size()) return null;
إرجاع this.data[0];
}
// أضف عنصرًا إلى الكومة Push(x){
this.data.push(x);
this.shiftUp(this.data. length-1);
}
// قم بإخراج العنصر الأول من الكومة pop(){
if(!this.size()) return null;
Let res = this.data[0];
إذا (هذا.الحجم () == 1) {
this.data.pop();
}
آخر {
this.data[0] = this.data[this.data. length-1];
this.data.length = this.data. length-1;
this.shiftDown(0);
}
دقة العودة؛
}
} Let arr = [2,9,8,6,3,10,5,7,4,1];
دع شركات = (أ، ب) => أب؛
Let heap = new Heap(arr, comp);
دع الدقة = []؛
بينما (الكومة. الحجم ()) {
res.push(heap.pop());
}
console.log(res); يمكن أن يكون العنصر الموجود في arr كائنًا أيضًا.
حزم الدليل/المجدول في كود مصدر React هو الكود المرتبط بوحدة جدولة المهام في React.
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src/Scheduler.js
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src /SchedulerMinHeap.js
/**
* حقوق الطبع والنشر (ج) لشركة Facebook, Inc. والشركات التابعة لها.
*
* تم ترخيص كود المصدر هذا بموجب ترخيص MIT الموجود في ملف
* ملف الترخيص في الدليل الجذر لهذه الشجرة المصدر.
*
* @تدفق صارم
*/
اكتب كومة = صفيف<Node>;
اكتب العقدة = {|
معرف: رقم،
مؤشر الفرز: رقم،
|};
دفع وظيفة التصدير (الكومة: الكومة، العقدة: العقدة): باطلة {
مؤشر ثابت = طول الكومة؛
heap.push(node);
siftUp(heap,node,index);
}
نظرة خاطفة على وظيفة التصدير (الكومة: الكومة): Node |.
const first = heap[0];
العودة أولا === غير محددة فارغة: أولا؛
}
دالة التصدير pop(heap: Heap): Node |.
const first = heap[0];
إذا (أولاً !== غير محدد) {
const last = heap.pop();
إذا (الأخير!== الأول) {
الكومة[0] = الأخيرة؛
siftDown(heap, last, 0);
}
العودة أولا؛
} آخر {
عودة فارغة؛
}
}
وظيفة siftUp(الكومة، العقدة، ط) {
دع الفهرس = i؛
بينما (صحيح) {
constparentIndex = (index - 1) >>> 1;
constparent = heap[parentIndex];
إذا (الوالد !== غير محدد && قارن(الأصل، العقدة) > 0) {
// الوالد أكبر من المواضع.
الكومة[parentIndex] = العقدة;
الكومة [الفهرس] = الأصل؛
مؤشر = الوالدينIndex؛
} آخر {
// الوالد أصغر.
يعود؛
}
}
}
وظيفة siftDown(الكومة، العقدة، ط) {
دع الفهرس = i؛
طول ثابت = طول الكومة؛
بينما (الفهرس <الطول) {
const leftIndex = (index + 1) * 2 - 1;
const left = heap[leftIndex];
const rightIndex = leftIndex + 1;
const right = heap[rightIndex];
// إذا كانت العقدة اليسرى أو اليمنى أصغر، فاستبدلها بالعقدة الأصغر منها.
إذا (يسار!== غير محدد && قارن(يسار، عقدة) < 0) {
إذا (يمين!== غير محدد && قارن(يمين، يسار) < 0) {
الكومة [الفهرس] = صحيح؛
الكومة[rightIndex] = العقدة;
مؤشر = حقيندكس؛
} آخر {
كومة [الفهرس] = اليسار؛
الكومة[leftIndex] = العقدة;
مؤشر = اليسار.
}
} وإلا إذا (يمين !== غير محدد && قارن(يمين، عقدة) < 0) {
الكومة [الفهرس] = صحيح؛
الكومة[rightIndex] = العقدة;
مؤشر = حقيندكس؛
} آخر {
// لا يوجد طفل أصغر.
يعود؛
}
}
}
مقارنة الدالة (أ، ب) {
// قارن فهرس الفرز أولاً، ثم معرف المهمة.
const diff = a.sortIndex - b.sortIndex;
إرجاع الفرق !== 0 ؟
} يختلف الحد الأدنى من الكومة التي قمنا بتنفيذها قليلاً عن التنفيذ في React، لكن الفكرة هي نفسها، فقط الكود مكتوب بشكل مختلف.
يتم تنفيذ جدولة المهام في React باستخدام الحد الأدنى من الكومة. إذا كان لدينا فهم معين للحد الأدنى من الكومة من قبل، فسوف نتعلم هذا المحتوى بشكل أسرع. شخصياً، أعتقد مدى أهمية تجميع المعرفة في المرحلة المبكرة، لكن هذه العملية قد تكون مملة. في الوقت الحالي، هل تعتقد أنك تعرف بعض الخوارزميات؟ في الواقع، هذه الخوارزميات هي مستوى مبتدئ، ولم تبدأ بعد؟ لأنه في سيناريو جدولة المهام في React، تكون المتطلبات التي سيتم تنفيذها واضحة جدًا، كما أن هياكل البيانات والخوارزميات التي سيتم استخدامها واضحة أيضًا. في بعض السيناريوهات الفعلية، نعرف المتطلبات المحددة، لكننا لا نعرف ما هي نتائج البيانات والخوارزميات التي يجب استخدامها، نحتاج إلى تجريد المتطلبات وتصميم هياكل بيانات وخوارزميات محددة بناءً على نموذج البيانات المجردة .