dsc 2 22 03 MLE gaussian lab bain trial jan19

MLE mit Normalverteilungen – Labor

Einführung

In diesem Labor werden wir die mathematischen Formeln, die wir in der vorherigen Lektion gesehen haben, in die Praxis umsetzen, um zu sehen, wie MLE mit Normalverteilungen funktioniert.

Ziele

Sie können:

• Verstehen und beschreiben Sie, wie MLE mit Normalverteilungen funktioniert
• Passen Sie eine Normalverteilung an gegebene Daten an und identifizieren Sie Mittelwert und Varianz
• Vergleichen Sie visuell die angepasste Verteilung mit der tatsächlichen Verteilung

Hinweis: *Eine detaillierte Ableitung aller MLE-Gleichungen mit Beweisen finden Sie auf dieser Website. *

MLE in Python

Sehen wir uns unten ein Beispiel für MLE und Verteilungsanpassungen mit Python an. Hier berechnet scipy.stats.norm.fit die Verteilungsparameter mithilfe der Maximum-Likelihood-Schätzung.

Importieren Sie die erforderlichen Bibliotheken

 from scipy . stats import norm # for generating sample data and fitting distributions
import matplotlib . pyplot as plt
plt . style . use ( 'seaborn' )
import numpy as np

Generieren Sie ein Array mit 200 Zufallsstichproben aus einem normalen Abstand mit Mittelwert 0 und Standardwert 1

 sample = None

Verteilungsanpassung durch MLE

- Verwenden Sie stats.norm.fit(data) um eine Verteilung an die oben genannten Daten anzupassen.

– Dies gibt über einen MLE-Ansatz eine Liste mit zwei Parametern zurück: (Mittelwert: Parameter[0] und Standard: Parameter[1]).

 param = None

#param[0], param[1]
# (0.08241224761452863, 1.002987490235812)

Berechnen Sie das PDF aus a) tatsächlichen Datenparametern b) angepassten Parametern mit x = np.linspace(-5,5,100)

 x = np . linspace ( - 5 , 5 , 100 )

# Generate the pdf from fitted parameters (fitted distribution)
fitted_pdf = None
# Generate the pdf without fitting (normal distribution non fitted)
normal_pdf = None

Visualisieren Sie beide PDFs

 # Your code here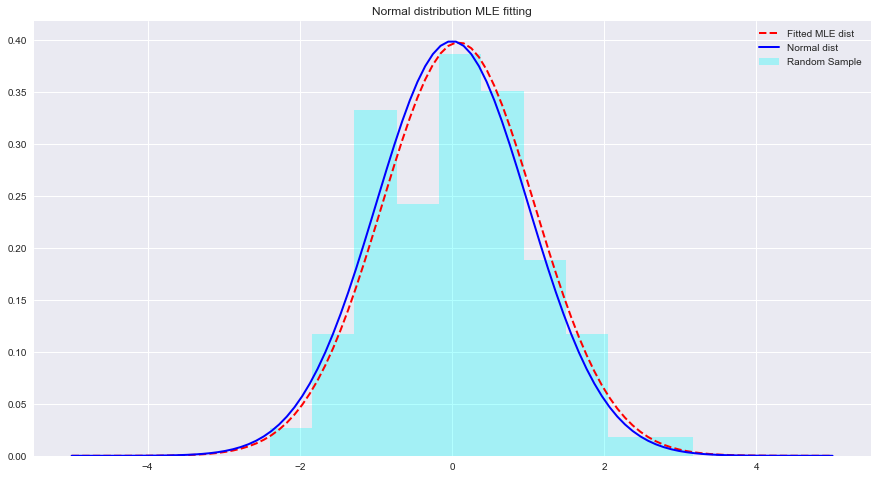 

 #  Your comments/observations 

Zusammenfassung

In dieser kurzen Übung haben wir die Bayes'sche Einstellung in einem Gauß'schen Kontext betrachtet, dh wenn die zugrunde liegenden Zufallsvariablen normalverteilt sind. Wir haben gelernt, dass MLE die unbekannten Parameter einer Normalverteilung schätzen kann, indem es die Wahrscheinlichkeit des erwarteten Mittelwerts maximiert. Der erwartete Mittelwert kommt dem Mittelwert einer nicht angepassten Normalverteilung innerhalb dieses Parameterraums sehr nahe. Wir werden dieses Verständnis weiterentwickeln und lernen, wie solche Schätzungen durchgeführt werden, um Mittelwerte für eine Reihe von in der Datenverteilung vorhandenen Klassen mithilfe des Naive-Bayes-Klassifikators zu schätzen.