

PyPortfolioOpt ist eine Bibliothek, die Portfoliooptimierungsmethoden implementiert, einschließlich klassischer Mittelwert-Varianz-Optimierungstechniken und Black-Litterman-Allokation sowie neuerer Entwicklungen auf diesem Gebiet wie Schrumpfung und hierarchische Risikoparität.
Es ist umfangreich und dennoch leicht erweiterbar und kann sowohl für Gelegenheitsinvestoren als auch für Profis nützlich sein, die ein einfaches Prototyping-Tool suchen. Egal, ob Sie ein fundamentalorientierter Investor sind, der eine Handvoll unterbewerteter Picks identifiziert hat, oder ein algorithmischer Trader, der über einen Korb von Strategien verfügt, PyPortfolioOpt kann Ihnen dabei helfen, Ihre Alpha-Quellen auf risikoeffiziente Weise zu kombinieren.
PyPortfolioOpt wurde im Journal of Open Source Software veröffentlicht?
PyPortfolioOpt wird jetzt von Tuan Tran verwaltet.
Besuchen Sie die Dokumentation auf ReadTheDocs, um einen detaillierten Einblick in das Projekt zu erhalten, oder schauen Sie sich das Kochbuch an, um einige Beispiele zu sehen, die den gesamten Prozess vom Herunterladen der Daten bis zum Aufbau eines Portfolios zeigen.
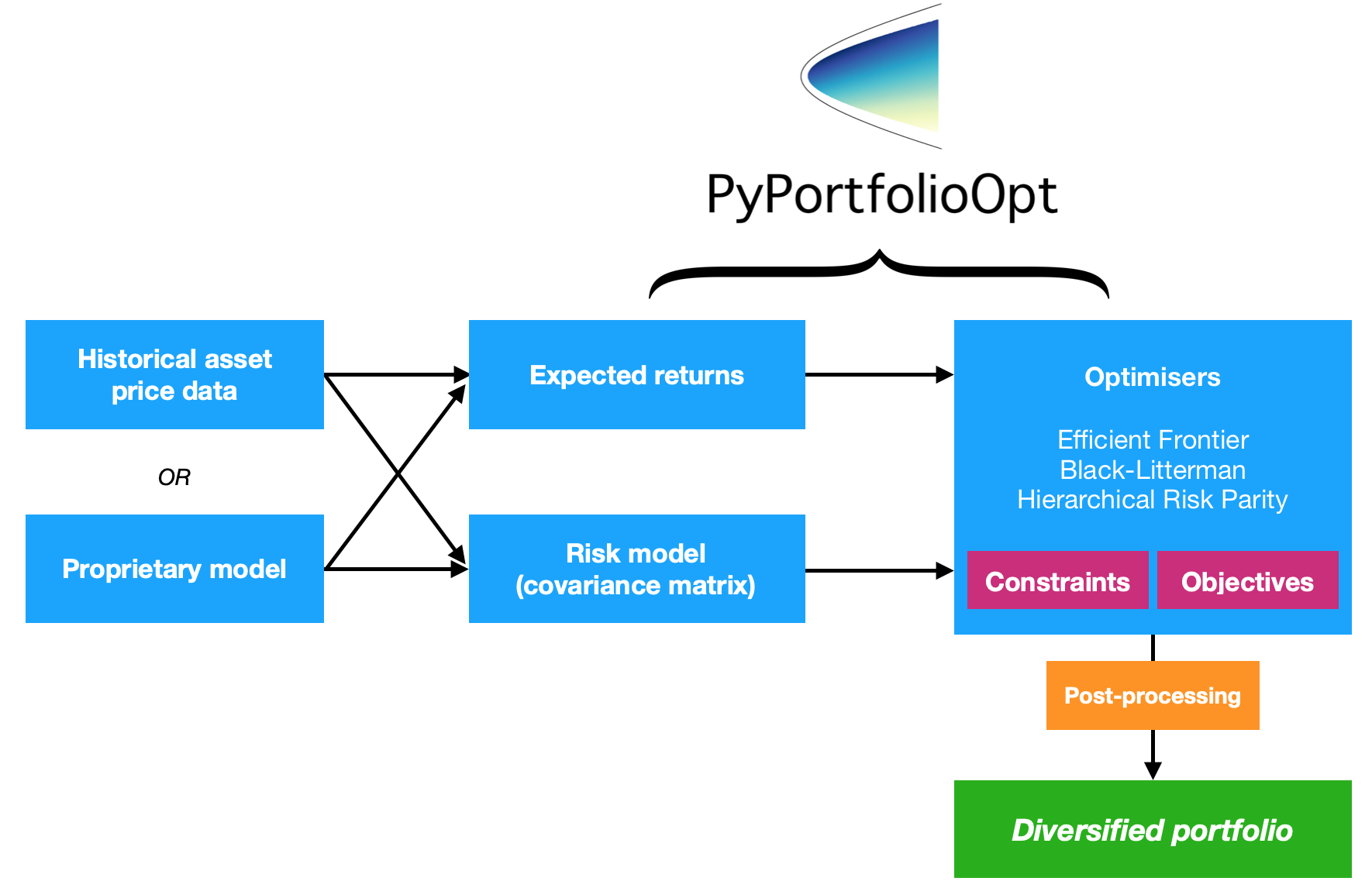
Wenn Sie interaktiv mit PyPortfolioOpt in Ihrem Browser spielen möchten, können Sie Binder hier starten. Die Einrichtung dauert eine Weile, aber Sie können die Kochbuchrezepte ausprobieren, ohne sich mit allen Anforderungen auseinandersetzen zu müssen.
Hinweis: macOS-Benutzer müssen die Befehlszeilentools installieren.
Hinweis: Wenn Sie Windows verwenden, müssen Sie zuerst C++ installieren. (Download, Installationsanleitung)
Dieses Projekt ist auf PyPI verfügbar, was bedeutet, dass Sie einfach:
pip install PyPortfolioOpt(Möglicherweise müssen Sie separate Installationsanweisungen für cvxopt und cvxpy befolgen).
Es empfiehlt sich jedoch, einen Abhängigkeitsmanager in einer virtuellen Umgebung zu verwenden. Meine aktuelle Empfehlung ist, sich mit Gedichten vertraut zu machen und dann einfach loszulaufen
poetry add PyPortfolioOptAndernfalls klonen/laden Sie das Projekt herunter und führen Sie im Projektverzeichnis Folgendes aus:
python setup.py install PyPortfolioOpt unterstützt Docker. Erstellen Sie Ihren ersten Container mit docker build -f docker/Dockerfile . -t pypfopt . Sie können das Image verwenden, um Tests auszuführen oder sogar einen Jupyter-Server zu starten.
# iPython interpreter:
docker run -it pypfopt poetry run ipython
# Jupyter notebook server:
docker run -it -p 8888:8888 pypfopt poetry run jupyter notebook --allow-root --no-browser --ip 0.0.0.0
# click on http://127.0.0.1:8888/?token=xxx
# Pytest
docker run -t pypfopt poetry run pytest
# Bash
docker run -it pypfopt bashFür weitere Informationen lesen Sie bitte diesen Leitfaden.
Wenn Sie größere Änderungen vornehmen möchten, um dies in Ihr proprietäres System zu integrieren, ist es wahrscheinlich sinnvoll, dieses Repository zu klonen und nur den Quellcode zu verwenden.
git clone https://github.com/robertmartin8/PyPortfolioOptAlternativ könnten Sie Folgendes versuchen:
pip install -e git+https://github.com/robertmartin8/PyPortfolioOpt.gitHier ist ein Beispiel für reale Aktiendaten, das zeigt, wie einfach es ist, das Long-Only-Portfolio zu finden, das die Sharpe-Ratio (ein Maß für risikobereinigte Renditen) maximiert.
import pandas as pd
from pypfopt import EfficientFrontier
from pypfopt import risk_models
from pypfopt import expected_returns
# Read in price data
df = pd . read_csv ( "tests/resources/stock_prices.csv" , parse_dates = True , index_col = "date" )
# Calculate expected returns and sample covariance
mu = expected_returns . mean_historical_return ( df )
S = risk_models . sample_cov ( df )
# Optimize for maximal Sharpe ratio
ef = EfficientFrontier ( mu , S )
raw_weights = ef . max_sharpe ()
cleaned_weights = ef . clean_weights ()
ef . save_weights_to_file ( "weights.csv" ) # saves to file
print ( cleaned_weights )
ef . portfolio_performance ( verbose = True )Dies gibt die folgenden Gewichte aus:
{'GOOG': 0.03835,
'AAPL': 0.0689,
'FB': 0.20603,
'BABA': 0.07315,
'AMZN': 0.04033,
'GE': 0.0,
'AMD': 0.0,
'WMT': 0.0,
'BAC': 0.0,
'GM': 0.0,
'T': 0.0,
'UAA': 0.0,
'SHLD': 0.0,
'XOM': 0.0,
'RRC': 0.0,
'BBY': 0.01324,
'MA': 0.35349,
'PFE': 0.1957,
'JPM': 0.0,
'SBUX': 0.01082}
Expected annual return: 30.5%
Annual volatility: 22.2%
Sharpe Ratio: 1.28Das ist interessant, aber an sich nicht nützlich. PyPortfolioOpt bietet jedoch eine Methode, mit der Sie die oben genannten kontinuierlichen Gewichtungen in eine tatsächliche Zuteilung umwandeln können, die Sie kaufen können. Geben Sie einfach die aktuellsten Preise und die gewünschte Portfoliogröße ein (in diesem Beispiel 10.000 US-Dollar):
from pypfopt . discrete_allocation import DiscreteAllocation , get_latest_prices
latest_prices = get_latest_prices ( df )
da = DiscreteAllocation ( weights , latest_prices , total_portfolio_value = 10000 )
allocation , leftover = da . greedy_portfolio ()
print ( "Discrete allocation:" , allocation )
print ( "Funds remaining: ${:.2f}" . format ( leftover ))12 out of 20 tickers were removed
Discrete allocation: {'GOOG': 1, 'AAPL': 4, 'FB': 12, 'BABA': 4, 'BBY': 2,
'MA': 20, 'PFE': 54, 'SBUX': 1}
Funds remaining: $ 11.89Haftungsausschluss: Nichts an diesem Projekt stellt eine Anlageberatung dar und der Autor übernimmt keine Verantwortung für Ihre späteren Anlageentscheidungen. Weitere Informationen finden Sie in der Lizenz.
Der Aufsatz von Harry Markowitz aus dem Jahr 1952 ist der unbestreitbare Klassiker, der die Portfoliooptimierung von einer Kunst in eine Wissenschaft verwandelte. Die wichtigste Erkenntnis besteht darin, dass man durch die Kombination von Vermögenswerten mit unterschiedlichen erwarteten Renditen und Volatilitäten eine mathematisch optimale Allokation festlegen kann, die das Risiko für eine Zielrendite minimiert – die Menge aller dieser optimalen Portfolios wird als Effizienzgrenze bezeichnet.
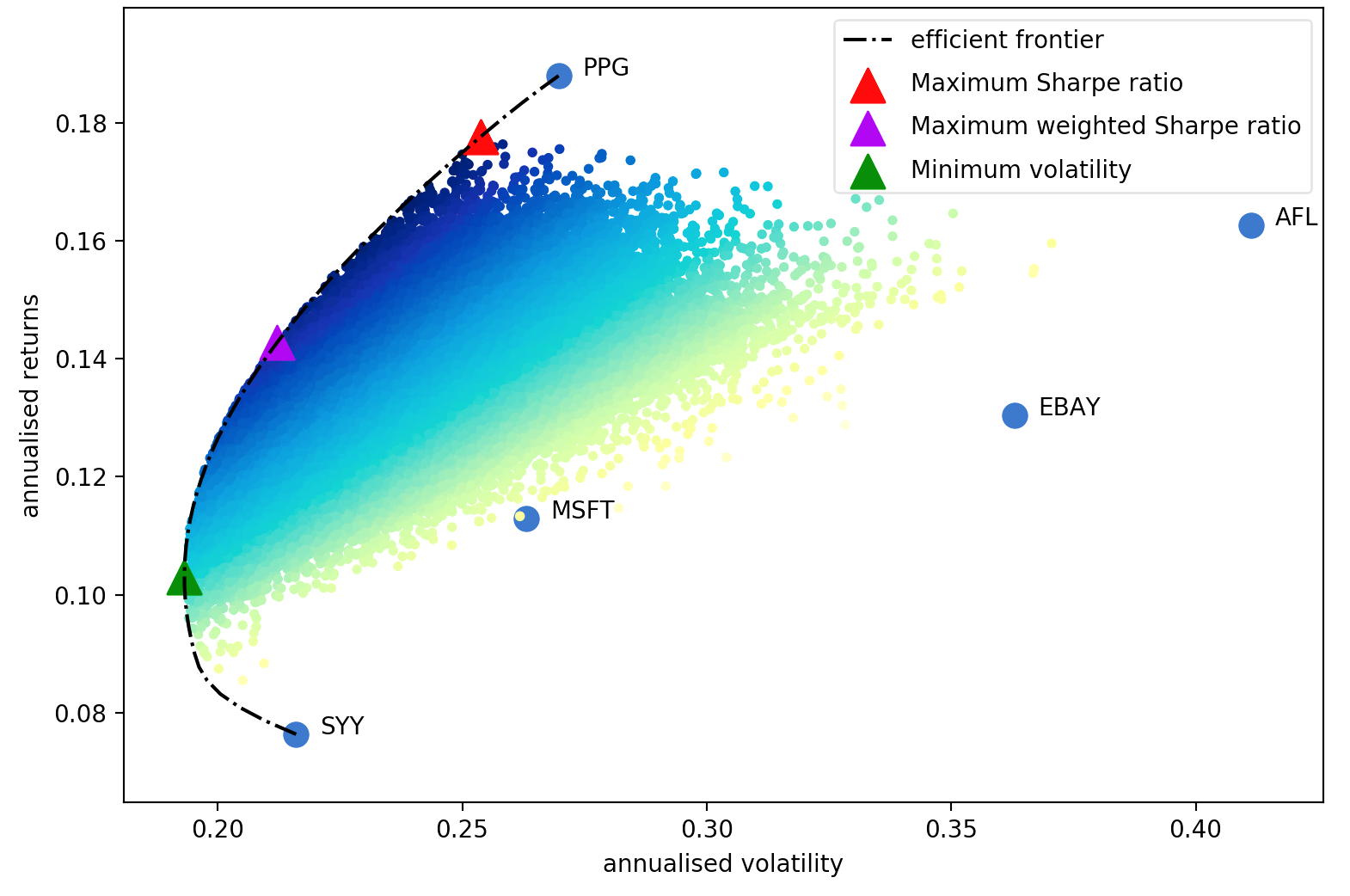
Obwohl es in diesem Bereich viele Fortschritte gegeben hat, sind die Kernideen von Markowitz auch mehr als ein halbes Jahrhundert später immer noch von grundlegender Bedeutung und werden in vielen Portfoliomanagementfirmen täglich angewendet. Der Hauptnachteil der Mittelwert-Varianz-Optimierung besteht darin, dass die theoretische Behandlung Kenntnisse über die erwarteten Renditen und die zukünftigen Risikoeigenschaften (Kovarianz) der Vermögenswerte erfordert. Wenn wir die erwarteten Renditen einer Aktienlaufzeit wüssten, wäre das natürlich viel einfacher, aber das Ganze ist, dass Aktienrenditen bekanntermaßen schwer vorherzusagen sind. Als Ersatz können wir Schätzungen der erwarteten Rendite und Kovarianz auf der Grundlage historischer Daten ableiten. Dabei verlieren wir zwar die theoretischen Garantien von Markowitz, aber je näher unsere Schätzungen an den tatsächlichen Werten liegen, desto besser wird unser Portfolio sein.
Somit bietet dieses Projekt vier Hauptfunktionen (obwohl sie natürlich eng miteinander verbunden sind).
Ein wichtiges Designziel von PyPortfolioOpt ist die Modularität – der Benutzer sollte in der Lage sein, seine Komponenten auszutauschen und gleichzeitig das von PyPortfolioOpt bereitgestellte Framework zu nutzen.
In diesem Abschnitt beschreiben wir einige der verfügbaren Funktionen von PyPortfolioOpt. Weitere Beispiele finden Sie in den Jupyter-Notizbüchern hier. Eine weitere gute Ressource sind die Tests.
Eine weitaus umfassendere Version davon sowie mögliche Erweiterungen für fortgeschrittenere Benutzer finden Sie auf ReadTheDocs.
Die Kovarianzmatrix kodiert nicht nur die Volatilität eines Vermögenswerts, sondern auch dessen Korrelation mit anderen Vermögenswerten. Dies ist wichtig, denn um die Vorteile der Diversifizierung zu nutzen (und damit die Rendite pro Risikoeinheit zu steigern), sollten die Vermögenswerte im Portfolio möglichst unkorreliert sein.
sklearn.covariance bereitgestellt werden.constant_variance , single_factor und constant_correlation .sklearn.covariance 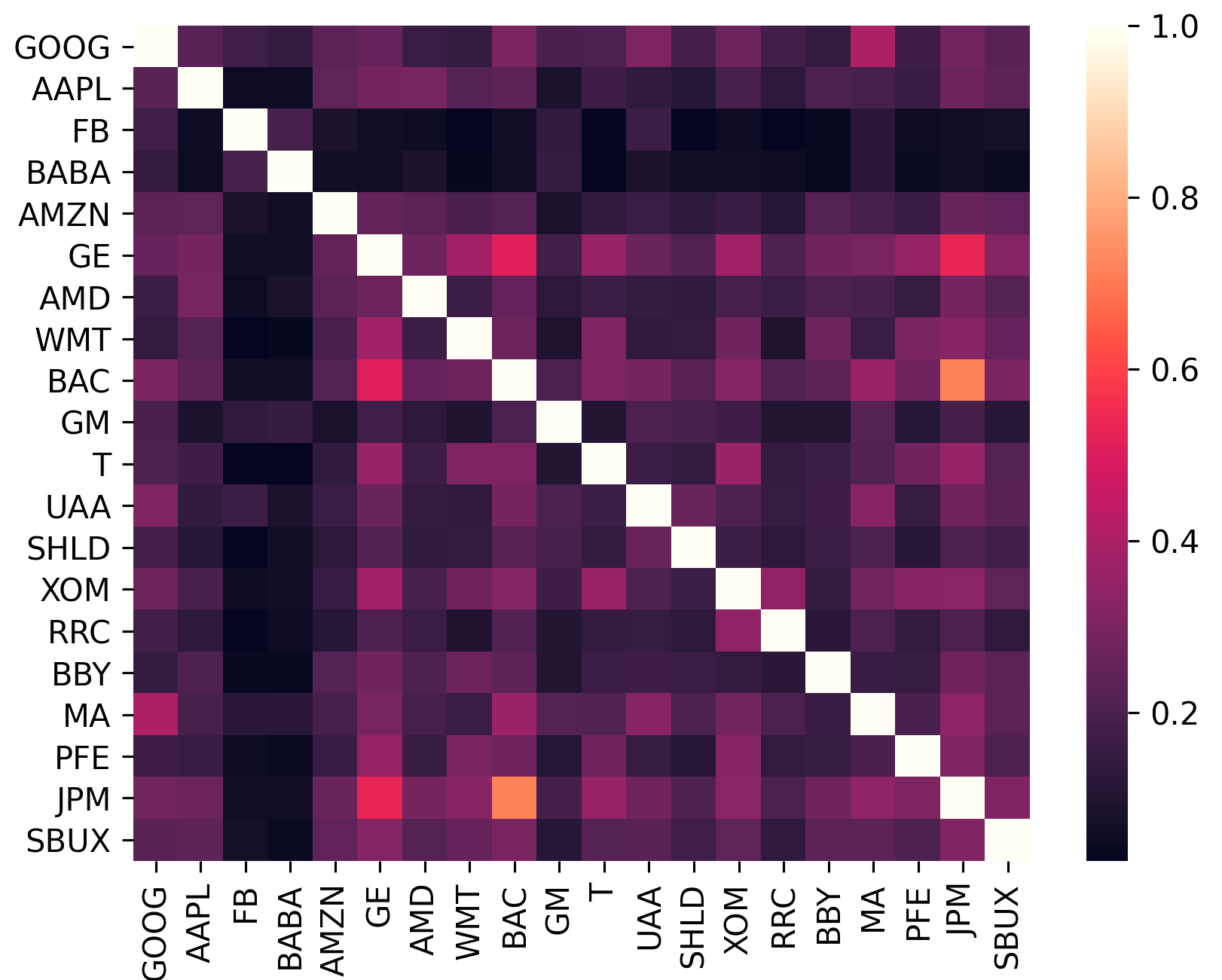
(Dieses Diagramm wurde mit plotting.plot_covariance erstellt)
ef = EfficientFrontier ( mu , S , weight_bounds = ( - 1 , 1 ))efficient_risk und efficient_return bietet PyPortfolioOpt eine Option zur Bildung eines marktneutralen Portfolios (d. h. die Gewichtungen summieren sich auf Null). Dies ist für das Max-Sharpe-Portfolio und das Min-Volatility-Portfolio nicht möglich, da sie in diesen Fällen in Bezug auf die Hebelwirkung nicht invariant sind. Marktneutralität erfordert negative Gewichte: ef = EfficientFrontier ( mu , S , weight_bounds = ( - 1 , 1 ))
ef . efficient_return ( target_return = 0.2 , market_neutral = True ) ef = EfficientFrontier ( mu , S , weight_bounds = ( 0 , 0.1 )) Ein Problem bei der Mittelwert-Varianz-Optimierung besteht darin, dass sie zu vielen Nullgewichten führt. Während diese innerhalb der Stichprobe „optimal“ sind, gibt es zahlreiche Untersuchungen, die zeigen, dass diese Eigenschaft dazu führt, dass Portfolios mit mittlerer Varianz schlechter abschneiden als außerhalb der Stichprobe. Zu diesem Zweck habe ich eine Zielfunktion eingeführt, die die Anzahl vernachlässigbarer Gewichte für jede der Zielfunktionen reduzieren kann. Im Wesentlichen fügt es eine Strafe (parametrisiert durch gamma ) für kleine Gewichte hinzu, mit einem Begriff, der genau wie die L2-Regularisierung beim maschinellen Lernen aussieht. Möglicherweise müssen mehrere gamma ausprobiert werden, um die gewünschte Anzahl nicht vernachlässigbarer Gewichtungen zu erreichen. Für das Testportfolio von 20 Wertpapieren ist gamma ~ 1 ausreichend
ef = EfficientFrontier ( mu , S )
ef . add_objective ( objective_functions . L2_reg , gamma = 1 )
ef . max_sharpe ()Ab Version 0.5.0 unterstützen wir nun die Vermögensallokation nach Black-Litterman, die es Ihnen ermöglicht, eine vorherige Renditeschätzung (z. B. die vom Markt implizierten Renditen) mit Ihren eigenen Ansichten zu kombinieren, um eine spätere Schätzung zu erstellen. Dies führt zu viel besseren Schätzungen der erwarteten Renditen als nur die Verwendung der durchschnittlichen historischen Rendite. Sehen Sie sich die Dokumente an, um eine Diskussion der Theorie sowie Ratschläge zur Formatierung von Eingaben zu erhalten.
S = risk_models . sample_cov ( df )
viewdict = { "AAPL" : 0.20 , "BBY" : - 0.30 , "BAC" : 0 , "SBUX" : - 0.2 , "T" : 0.131321 }
bl = BlackLittermanModel ( S , pi = "equal" , absolute_views = viewdict , omega = "default" )
rets = bl . bl_returns ()
ef = EfficientFrontier ( rets , S )
ef . max_sharpe () Die oben genannten Funktionen beziehen sich hauptsächlich auf die Lösung von Problemen der Mittelwert-Varianz-Optimierung mittels quadratischer Programmierung (obwohl dies von cvxpy übernommen wird). Wir bieten jedoch auch verschiedene Optimierer an:
Weitere Informationen finden Sie in der Dokumentation.
Tests werden in Pytest geschrieben (meiner Meinung nach viel intuitiver als unittest und die Varianten), und ich habe versucht, eine nahezu 100-prozentige Abdeckung sicherzustellen. Führen Sie die Tests aus, indem Sie zum Paketverzeichnis navigieren und einfach pytest in der Befehlszeile ausführen.
PyPortfolioOpt stellt einen Testdatensatz der täglichen Renditen für 20 Ticker bereit:
[ 'GOOG' , 'AAPL' , 'FB' , 'BABA' , 'AMZN' , 'GE' , 'AMD' , 'WMT' , 'BAC' , 'GM' ,
'T' , 'UAA' , 'SHLD' , 'XOM' , 'RRC' , 'BBY' , 'MA' , 'PFE' , 'JPM' , 'SBUX' ]Diese Ticker wurden informell ausgewählt, um mehrere Kriterien zu erfüllen:
Derzeit wurden in den Tests nicht alle Randfälle und Kombinationen von Zielfunktionen und Parametern untersucht. Es wurde jedoch getestet, dass jede Methode und jeder Parameter wie vorgesehen funktioniert.
Wenn Sie PyPortfolioOpt für veröffentlichte Arbeiten verwenden, zitieren Sie bitte das JOSS-Papier.
Zitatzeichenfolge:
Martin, R. A., (2021). PyPortfolioOpt: portfolio optimization in Python. Journal of Open Source Software, 6(61), 3066, https://doi.org/10.21105/joss.03066
BibTex::
@article { Martin2021 ,
doi = { 10.21105/joss.03066 } ,
url = { https://doi.org/10.21105/joss.03066 } ,
year = { 2021 } ,
publisher = { The Open Journal } ,
volume = { 6 } ,
number = { 61 } ,
pages = { 3066 } ,
author = { Robert Andrew Martin } ,
title = { PyPortfolioOpt: portfolio optimization in Python } ,
journal = { Journal of Open Source Software }
}Beiträge sind herzlich willkommen . Weitere Informationen finden Sie im Beitragsleitfaden.
Ich möchte allen Menschen danken, die seit der Veröffentlichung im Jahr 2018 zu PyPortfolioOpt beigetragen haben. Besonderer Dank geht an: