
Dies sind die Codierungsimplementierungen des DSA.js-Buchs und des Repos für das NPM-Paket.
In diesem Repository finden Sie die Implementierung von Algorithmen und Datenstrukturen in JavaScript. Dieses Material kann als Referenzhandbuch für Entwickler verwendet werden oder Sie können bestimmte Themen vor einem Interview auffrischen. Außerdem können Sie Ideen finden, um Probleme effizienter zu lösen.
Sie können das Repo klonen oder den Code von NPM installieren:
npm install dsa.jsund dann können Sie es in Ihre Programme oder CLI importieren
const { LinkedList , Queue , Stack } = require ( 'dsa.js' ) ;Eine Liste aller verfügbaren Datenstrukturen und Algorithmen finden Sie unter index.js.
Algorithmen sind ein unverzichtbarer Werkzeugkasten für jeden Programmierer.
Sie müssen auf die Laufzeit von Algorithmen achten, wenn Sie Daten sortieren, in einem großen Datensatz nach einem Wert suchen, Daten transformieren, Ihren Code für viele Benutzer skalieren müssen, um nur einige zu nennen. Algorithmen sind nur die Schritte, die Sie befolgen, um ein Problem zu lösen, während Datenstrukturen der Ort sind, an dem Sie die Daten für eine spätere Bearbeitung speichern. Beides zusammen ergibt Programme.
Algorithmen + Datenstrukturen = Programme.
Die meisten Programmiersprachen und Bibliotheken bieten tatsächlich Implementierungen für grundlegende Datenstrukturen und Algorithmen. Um Datenstrukturen jedoch richtig nutzen zu können, müssen Sie die Kompromisse kennen, um das beste Tool für die Aufgabe auszuwählen.
Dieses Material wird Ihnen Folgendes beibringen:
Der gesamte Code und die Erklärungen sind in diesem Repo verfügbar. Sie können die Links und Codebeispiele im Ordner (src) durchstöbern. Allerdings werden die Inline-Codebeispiele nicht erweitert (aufgrund der Asciidoc-Einschränkungen von Github), aber Sie können dem Pfad folgen und die Implementierung sehen.
Hinweis: Wenn Sie die Informationen lieber linearer konsumieren möchten, ist das Buchformat für Sie besser geeignet.
Die Themen sind in vier Hauptkategorien unterteilt, wie Sie unten sehen können:
Informatik-Nuggets ohne all den Hokuspokus. (Zum Vergrößern anklicken)
Informatik-Nuggets ohne all den Hokuspokus
Erfahren Sie anhand von Codebeispielen, wie Sie die Laufzeit berechnen
Erfahren Sie, wie Sie Algorithmen mithilfe der Big-O-Notation vergleichen. (Zum Vergrößern anklicken)
Erfahren Sie, wie Sie Algorithmen mithilfe der Big-O-Notation vergleichen.
Vergleich von Algorithmen mit Big-O-Notation
Nehmen wir an, Sie möchten die Duplikate in einem Array finden. Mit der Big-O-Notation können wir verschiedene Lösungen vergleichen, die das gleiche Problem lösen, aber einen großen Unterschied in der Dauer haben, die dafür benötigt wird.
- Optimale Lösung mithilfe einer Karte
- Duplikate in einem Array finden (naiver Ansatz)
8 Beispiele, um mit Code zu erklären, wie man die Zeitkomplexität berechnet. (Zum Vergrößern anklicken)
8 Beispiele, um mit Code zu erklären, wie man die Zeitkomplexität berechnet
Die häufigsten zeitlichen Komplexitäten
Zeitkomplexitätsdiagramm
Verstehen Sie die Besonderheiten der gängigsten Datenstrukturen. (Zum Vergrößern anklicken)
Verstehen Sie die Besonderheiten der gängigsten Datenstrukturen
Arrays: In den meisten Sprachen integriert, daher hier nicht implementiert. Array-Zeitkomplexität
Verknüpfte Liste: Jeder Datenknoten hat einen Link zum nächsten (und vorherigen). Code | Zeitkomplexität verknüpfter Listen
Warteschlange: Der Datenfluss erfolgt nach dem FIFO-Prinzip (First In, First Out). Code | Komplexität der Warteschlangenzeit
Stapel: Der Datenfluss erfolgt nach dem Last-In-First-Out-Prinzip (LIFO). Code | Komplexität der Stapelzeit
Wann sollte ein Array oder eine verknüpfte Liste verwendet werden? Kennen Sie die Kompromisse. (Zum Vergrößern anklicken)
Wann sollte ein Array oder eine verknüpfte Liste verwendet werden? Kennen Sie die Kompromisse
Verwenden Sie Arrays, wenn…
- Sie müssen schnell (mithilfe eines Index) auf Daten in zufälliger Reihenfolge zugreifen.
- Ihre Daten sind mehrdimensional (z. B. Matrix, Tensor).
Verwenden Sie verknüpfte Listen, wenn:
- Sie greifen nacheinander auf Ihre Daten zu.
- Sie möchten Speicher sparen und nur dann Speicher zuweisen, wenn Sie ihn benötigen.
- Sie benötigen eine konstante Zeit zum Entfernen/Hinzufügen von Extremen der Liste.
- wenn die Größenanforderung unbekannt ist – dynamischer Größenvorteil
Erstellen Sie eine Liste, einen Stapel und eine Warteschlange. (Zum Vergrößern anklicken)
Erstellen Sie eine Liste, einen Stapel und eine Warteschlange von Grund auf
Erstellen Sie eine dieser Datenstrukturen von Grund auf:
- Verlinkte Liste
- Stapel
- Warteschlange
Verstehen Sie eine der vielseitigsten Datenstrukturen überhaupt: Hash Maps. (Zum Vergrößern anklicken)
HashMaps
Erfahren Sie, wie Sie verschiedene Arten von Karten implementieren, z. B.:
- HashMap
- TreeMap
Erfahren Sie außerdem den Unterschied zwischen den verschiedenen Maps-Implementierungen:
HashMapist zeiteffizienter. EineTreeMapist platzsparender.- Die Komplexität
TreeMap-Suche beträgt O(log n) , während eine optimierteHashMapim Durchschnitt O(1) beträgt.- Die Schlüssel von
HashMapliegen in der Einfügereihenfolge vor (oder sind je nach Implementierung zufällig). Die Schlüssel vonTreeMapsind immer sortiert.TreeMapbietet einige statistische Daten kostenlos an, z. B. Minimum ermitteln, Maximum ermitteln, Median ermitteln, Schlüsselbereiche ermitteln.HashMapnicht.TreeMaphat garantiert immer ein O(log n) , währendHashMaps eine amortisierte Zeit von O(1) hat, aber im seltenen Fall eines erneuten Aufwärmens würde es ein O(n) erfordern.Kennen Sie die Eigenschaften von Diagrammen und Bäumen. (Zum Vergrößern anklicken)
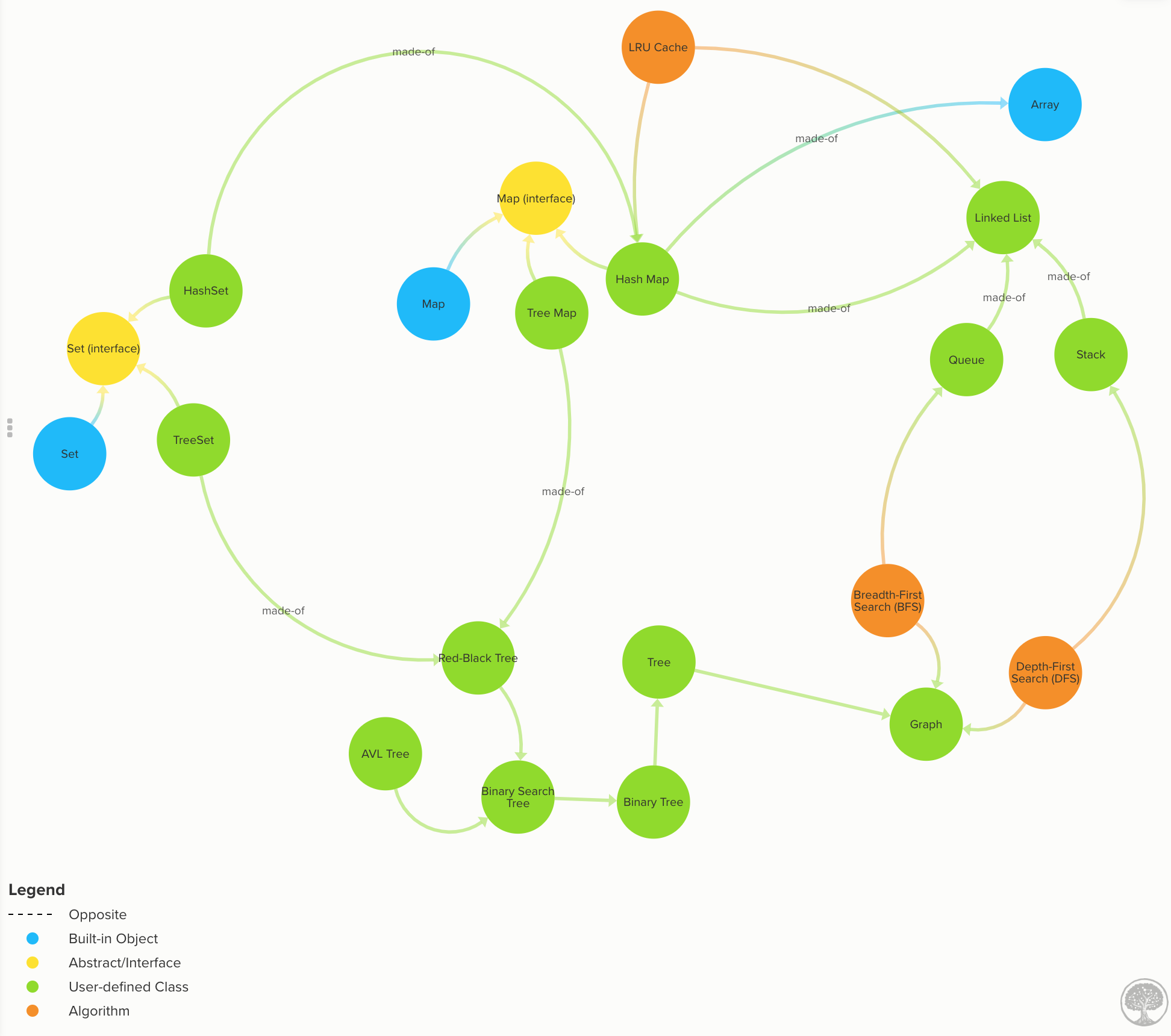
Kennen Sie die Eigenschaften von Diagrammen und Bäumen
Grafiken
Kennen Sie alle Diagrammeigenschaften mit vielen Bildern und Illustrationen.
Diagramme : Datenknoten , die eine Verbindung oder Kante zu null oder mehr benachbarten Knoten haben können. Im Gegensatz zu Bäumen können Knoten mehrere übergeordnete Knoten (Schleifen) haben. Code | Zeitkomplexität des Diagramms
Bäume
Lernen Sie alle verschiedenen Baumarten und ihre Eigenschaften kennen.
Bäume : Datenknoten haben null oder mehr benachbarte Knoten, auch untergeordnete Knoten genannt. Jeder Knoten kann nur einen übergeordneten Knoten haben, andernfalls handelt es sich um ein Diagramm und nicht um einen Baum. Code | Dokumente
Binärbäume : Wie ein Baum, können aber höchstens zwei Kinder haben. Code | Dokumente
Binäre Suchbäume (BST): wie ein Binärbaum, aber die Knotenwerte behalten die Reihenfolge
left < parent < rightbei. Code | BST ZeitkomplexitätAVL-Bäume : Selbstbalancierter BST zur Maximierung der Suchzeit. Code | AVL Tree-Dokumente | Dokumentation zum Selbstausgleich und zur Baumrotation
Rot-Schwarze Bäume : Selbstbalancierter BST, lockerer als AVL, um die Einfügungsgeschwindigkeit zu maximieren. Code
Implementieren Sie einen binären Suchbaum für schnelle Suchvorgänge.
Implementieren Sie einen binären Suchbaum für schnelle Suchvorgänge
Erfahren Sie, wie Sie Werte in einem Baum hinzufügen/entfernen/aktualisieren:
Wie bringt man einen Baum ins Gleichgewicht?
Von unausgeglichenem BST zu ausgeglichenem BST
1 2 / 2 => 1 3 3
Bleiben Sie mit 7 einfachen Schritten nie bei der Lösung eines Problems hängen. (Zum Vergrößern anklicken)
Bleiben Sie mit 8 einfachen Schritten nie stecken, wenn Sie ein Problem lösen
- Verstehe das Problem
- Erstellen Sie ein einfaches Beispiel (noch keine Randfälle)
- Brainstorming-Lösungen (gieriger Algorithmus, Divide and Conquer, Backtracking, Brute Force)
- Testen Sie Ihre Antwort anhand des einfachen Beispiels (mental)
- Optimieren Sie die Lösung
- Code schreiben. Ja, jetzt können Sie programmieren.
- Testen Sie Ihren geschriebenen Code
- Analysieren Sie die räumliche und zeitliche Komplexität und sorgen Sie für weitere Optimierungen.
Alle Details hier
Beherrschen Sie die gängigsten Sortieralgorithmen (Mergesort, Quicksort usw.) (Zum Vergrößern anklicken)
Beherrschen Sie die beliebtesten Sortieralgorithmen
Wir werden drei wesentliche Sortieralgorithmen O(n^2) untersuchen, die einen geringen Overhead haben:
Blasensortierung. Code | Dokumente
Einfügungssortierung. Code | Dokumente
Auswahlsortierung. Code | Dokumente
und diskutieren Sie dann effiziente Sortieralgorithmen O(n log n) wie:
Sortierung zusammenführen. Code | Dokumente
Quicksort. Code | Dokumente
Lernen Sie verschiedene Ansätze zur Lösung von Problemen wie „Teile und herrsche“, dynamische Programmierung, gierige Algorithmen und Backtracking. (Zum Vergrößern anklicken)
Lernen Sie verschiedene Ansätze zur Lösung algorithmischer Probleme kennen
Wir werden die folgenden Techniken zur Lösung von Algorithmenproblemen diskutieren:
- Gierige Algorithmen: Trifft gierige Entscheidungen mithilfe von Heuristiken, um die beste Lösung zu finden, ohne zurückzublicken.
- Dynamische Programmierung: eine Technik zur Beschleunigung rekursiver Algorithmen, wenn es viele überlappende Teilprobleme gibt. Es verwendet Memoisierung, um Doppelarbeiten zu vermeiden.
- Teilen und erobern: Teilen Sie Probleme in kleinere Teile, lösen Sie jedes Teilproblem und fügen Sie dann die Ergebnisse zusammen.
- Backtracking: Alle (oder einige) möglichen Pfade durchsuchen. Es stoppt jedoch und Sie kehren zurück, sobald Sie bemerken, dass die aktuelle Lösung nicht funktioniert.
- Brute Force : Generiert alle möglichen Lösungen und probiert sie alle aus. (Verwenden Sie es als letzten Ausweg oder als Ausgangspunkt).
Als Programmierer müssen wir jeden Tag Probleme lösen. Wenn Sie Probleme gut lösen wollen, ist es gut, über ein breites Lösungsspektrum Bescheid zu wissen. Oft ist es effizienter, sich mit vorhandenen Ressourcen vertraut zu machen, als selbst auf die Antwort zu stoßen. Je mehr Werkzeuge und Übung Sie haben, desto besser. Dieses Buch hilft Ihnen, die Kompromisse zwischen Datenstrukturen und die Gründe für die Leistung von Algorithmen zu verstehen.
Es gibt nicht viele Bücher über Algorithmen in JavaScript. Dieses Material füllt die Lücke. Außerdem ist es eine gute Übung :)
Ja, öffnen Sie ein Problem oder stellen Sie Fragen im [Slack-Kanal](https://dsajs-slackin.herokuapp.com).
Dieses Projekt ist auch als Buch erhältlich. Sie erhalten ein gut formatiertes PDF mit mehr als 180 Seiten + ePub- und Mobi-Version.
Kontaktieren Sie mich an einem der folgenden Orte!
@iAmAdrianMejiadsajs.slack.com