
und die Fiber-Aufgaben in React Bescheid wissen. Verschiedene Fiber-Aufgaben haben unterschiedliche Prioritäten, um Aufgaben mit hoher Priorität zuerst zu verarbeiten. Beispielsweise sind die Klicks und Eingaben des Benutzers Aufgaben mit hoher Priorität, da von den Vorgängen des Benutzers auf jeden Fall unmittelbare Auswirkungen erwartet werden, um das Benutzererlebnis zu verbessern. Beispielsweise muss die Priorität von Animationsereignissen niedriger sein. Nachdem eine neue Aufgabe mit hoher Priorität in die Warteschlange gelangt, muss React sie zuerst verarbeiten.
Um diese Aufgaben zu speichern, gibt es in React zwei Aufgabenpools.
// Aufgaben werden auf einem minimalen Heap gespeichert var taskQueue = []; var timerQueue = [];
taskQueue und timerQueue sind beide Arrays. Ersteres speichert Aufgaben, die sofort ausgeführt werden sollen, während letzteres Aufgaben speichert, die verzögert werden können.
var newTask = {
id: taskIdCounter++, // Aufgaben-ID markieren
Rückruf, // Rückruffunktion PriorityLevel, // Aufgabenpriorität startTime, // Aufgabenstartzeit, Zeitpunkt expirationTime, // Ablaufzeit, Zeitpunkt sortIndex: -1, // Aufgabensortierung, der Wert kommt aus der Ablaufzeit, also der Wert: Je kleiner der Wert, desto höher die Priorität}; Sobald eine neue Aufgabe in React eintrifft, wird zunächst currentTime verwendet, um die aktuelle Zeit aufzuzeichnen (performance.now() oder Date.now()). Verzögerungsparameter, dann beginnt die Ausführungszeit der Aufgabe startTime = currentTime + Verzögerung;. Wenn als nächstes startTime > currentTime festgelegt ist, beweist dies, dass die Aufgabe verschoben werden kann. Anschließend wird die Aufgabe in die timerQueue eingegeben, andernfalls in die taskQueue.
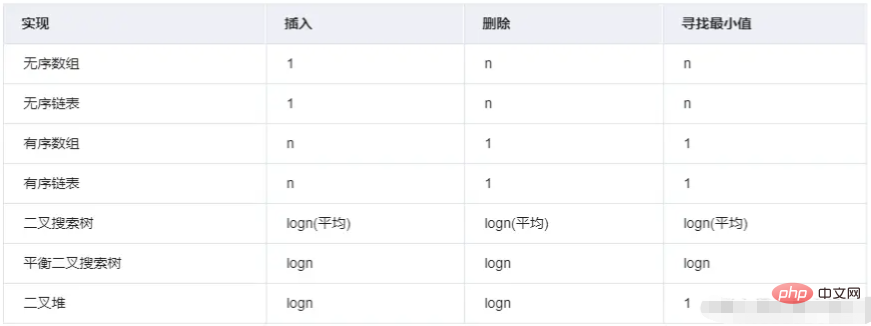
Wie findet React die Aufgabe mit der höchsten Priorität? Nehmen Sie taskQueue als Beispiel. Es handelt sich um einen dynamischen Aufgabenpool (Aufgabenwarteschlange) und die Datenform ist ein Array. Natürlich können Sie nach Priorität sortieren, d. h. Array.sort Wenn eine neue Aufgabe zur Warteschlange hinzugefügt wird, wird sie zuerst sortiert und dann wird die Aufgabe mit der höchsten Priorität gefunden und ausgeführt. Die durchschnittliche Zeitkomplexität von Array.sort beträgt jedoch O (nlogn), was nicht die beste Lösung ist.
SortIndex wird zum Sortieren in taskQueues newTask verwendet. Dies bedeutet, dass die Ablaufzeit umso kürzer ist, je höher die Priorität der Aufgabe ist Je kleiner die Zeit, desto kleiner ist natürlich auch der sortIndex. Tatsächlich handelt es sich hierbei um eine Prioritätswarteschlange .
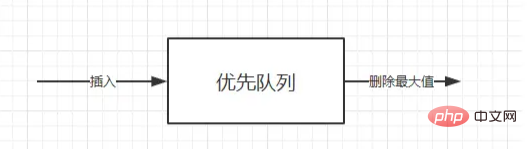
ist auch eine Art Warteschlange ( erstens ist es eine Warteschlange, und zweitens ist es eine Tail-in-first-out- Reihenfolge). Der einzige Unterschied besteht darin, dass die Reihenfolge der Warteschlangenentfernung in einigen Fällen auf der Priorität basiert Möglicherweise müssen Sie das minimale oder maximale Element im Elementsatz finden, indem Sie die Prioritätswarteschlange ADT verwenden. Die Prioritätswarteschlange ADT ist eine Datenstruktur, die das Einfügen und Löschen von Mindestwertoperationen (Zurückgeben und Löschen des Mindestelements) unterstützt Löschen des Maximalwertvorgangs (Zurückgeben und Löschen des minimalen Elements).
Wenn das Element mit dem kleinsten Schlüsselwert die höchste Priorität hat, wird diese Prioritätswarteschlange als aufsteigende Prioritätswarteschlange bezeichnet (d. h. das kleinste Element wird immer zuerst gelöscht). Wenn das Element mit dem größten Schlüsselwert die höchste Priorität hat, wird diese Art von Prioritätswarteschlange ebenfalls als absteigende Prioritätswarteschlange bezeichnet (dh das größte Element wird immer zuerst gelöscht, da diese beiden Typen symmetrisch sind). um sich auf eine davon zu konzentrieren, beispielsweise auf eine aufsteigende Prioritätswarteschlange.
Zum Beispiel : Als wir Tickets kauften, standen wir alle in der Warteschlange und hatten die gleiche Priorität, wer zuerst in der Warteschlange war. Aber dann kam ein Soldat und er hatte eine höhere Priorität und stand direkt in der Warteschlange . Die Vorderseite.
Um diese Funktion zu erreichen, wird in React ein minimaler Heap (kleiner Root-Heap, kleiner Top-Heap ...) verwendet. Das heißt, die TaskQueue wird in einen minimalen Heap umgewandelt, dann wird die oberste Aufgabe zur Ausführung herausgenommen, die TaskQueue wird gestapelt und als minimale Heap-Datenstruktur verwaltet. Beim Einfügen einer neuen Aufgabe in die TaskQueue muss diese ebenfalls gehäuft werden und immer als minimaler Heap beibehalten werden.
: An manchen Stellen wird der Heap als Prioritätswarteschlange bezeichnet (nicht korrekt). Erstens handelt es sich um eine Warteschlange mit den Merkmalen einer Warteschlange, d. h. „ First in, first out “. . Zweitens haben die Elemente in dieser Warteschlange Prioritäten, und diejenigen mit höheren Prioritäten werden zuerst eingestuft.
Genauer gesagt ist ein Heap eine Möglichkeit, eine Prioritätswarteschlange zu implementieren. Selbstverständlich können Priority Queues auch auf andere Art und Weise umgesetzt werden.
Wir haben zuvor gesagt, dass die Heap-Sortierung eine instabile Sortierung ist, aber taskQueue hofft, dass dieser Prozess stabil ist. Das heißt, wenn es möglich ist, dass die Ablaufzeit zweier Aufgaben gleich ist, hängt es davon ab, wer eintritt Erstens ist der Aufgabenpool der Wert der ID von newTask. Jedes Mal, wenn eine neue Aufgabe ankommt, wird die ID um 1 erhöht.
Funktion vergleichen(a, b) {
// Zuerst den Sortierindex und dann die Aufgaben-ID vergleichen.
const diff = a.sortIndex - b.sortIndex;
return diff !== 0 ? diff : a.id - b.id;
} Bevor wir den minimalen Heap verstehen, werfen wir einen Blick auf die Grundkenntnisse.
bezieht sich auf einen geordneten Baum, in dem der Grad der Knoten im Baum nicht größer als 2 ist. Es handelt sich um den einfachsten und wichtigsten Baum.
ist ein Binärbaum, in dem alle Knoten auf jeder Ebene zwei untergeordnete Knoten haben, mit Ausnahme der letzten Ebene, die keine untergeordneten Knoten hat.
Aus grafischer Sicht sieht ein vollständiger Binärbaum wie ein Dreieck aus.
Wenn die Anzahl der Ebenen eines Binärbaums K beträgt und die Gesamtzahl der Knoten (2^k) -1 beträgt, handelt es sich um einen vollständigen Binärbaum.
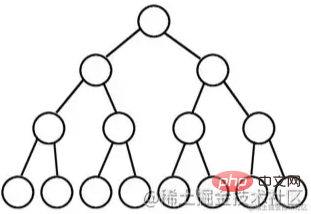
Ein vollständiger Binärbaum bedeutet „Töchter haben beide Seiten“ und ist sehr perfekt, daher wird er als vollständiger Binärbaum bezeichnet.
ohne Blattknoten beträgt der Grad aller Knoten 2. Mit anderen Worten: Der Grad aller Knoten kann nur 0 oder 2 sein.
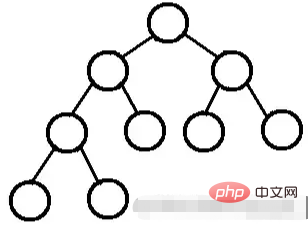
Ein perfekter Binärbaum hat entweder keine Kinder oder beide Kinder.
Der englische Originaltext von Full Binary Tree:
Ein vollständiger Binärbaum (FBT) ist ein Baum, in dem jeder Knoten außer den Blättern zwei untergeordnete Knoten hat.
Der englische Originaltext des perfekten Binärbaums:
Ein perfekter Binärbaum (PBT) ist ein Baum, bei dem sich alle Blattknoten in der gleichen Tiefe befinden Alle internen Knoten haben den Grad 2.
Alle ausländischen Bücher beziehen sich auf die frühesten übersetzten Lehrbücher zu vollständigen Binärbäumen und perfekten Binärbäumen, aber die frühesten übersetzten Artikel sind falsch übersetzt. Jetzt können wir in China nur dann Fehler machen, wenn sie falsch sind (jeder hat Unrecht, dann ist der Falsche auch richtig. Zum Beispiel Lobbyisten...). Wenn Sie diese beiden Konzepte mit ausländischen Freunden besprechen möchten, sollten Sie aufmerksam sein.
EinBinärbaum (CBT) ist ein Binärbaum, in dem jede Ebene, außer möglicherweise der letzten, vollständig gefüllt ist und alle Knoten so weit links wie möglich sind.
Ein Binärbaum mit n Knoten der Tiefe k, nummeriert die Knoten im Baum von oben nach unten und von links nach rechts. Wenn der Knoten mit der Nummer i (1≤i≤n) im Binärbaum mit dem Knoten mit der Nummer i im vollständigen Binärbaum ist, ist der Binärbaum gleich wird als vollständiger Binärbaum bezeichnet.
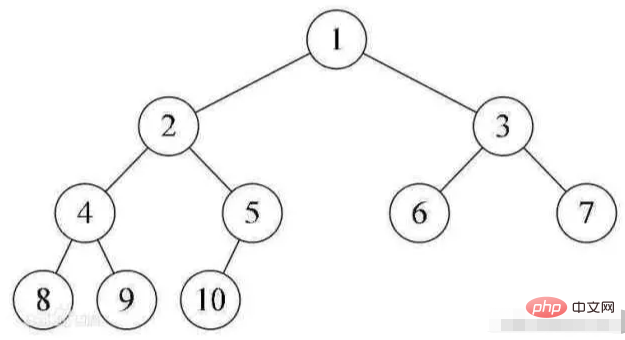
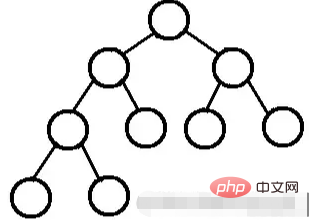
Der Heap erfüllt immer die folgenden Eigenschaften:
Knotens der kleine Root-Heap. In einem vollständigen Binärbaum sind alle Knoten größer (oder kleiner) als ihre untergeordneten Knoten, daher gibt es hier zwei Situationen: den maximalen Heap und den minimalen Heap.
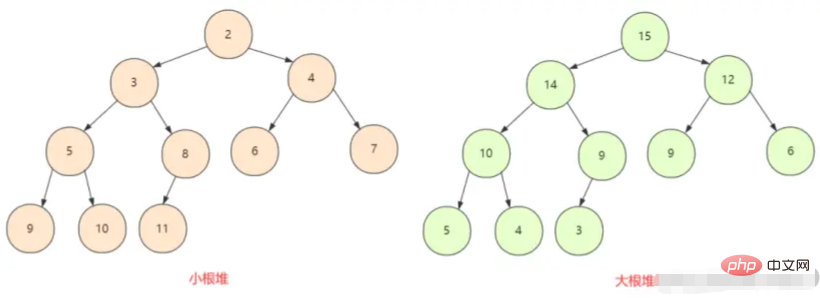
Der Heap ist normalerweise ein Array von Objekten, das als vollständiger Binärbaum betrachtet werden kann . Natürlich können Binärbäume auch durch Arrays dargestellt werden.
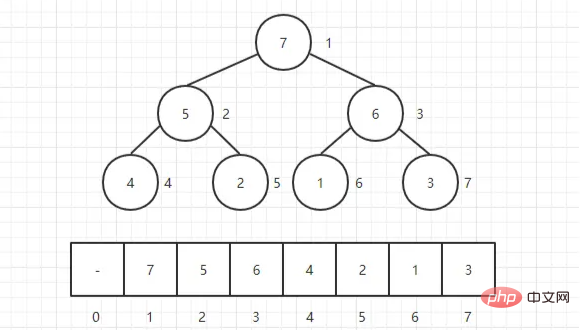
besteht darin, zuerst den Heap zu erstellen und ihn dann anzupassen.
Um einen Heapfür einen Binärbaum (Array-Darstellung)
Der Aufbau eines Heaps erfolgt nach O(n). ) Zeitkomplexitätsprozess.
① Beginnen Sie mit der Beurteilung des Austauschs nach unten (shiftDown), damit der aktuelle Knoten und das untergeordnete Element die Heap-Eigenschaften beibehalten können
. ② Ein gewöhnlicher Knotenaustausch stellt jedoch möglicherweise kein Problem dar, wenn der Austausch die Eigenschaften der Heap-Struktur zerstört des untergeordneten Knotens, dann muss der ausgetauschte Knoten erneut verschoben werden, bis er gestoppt wird.
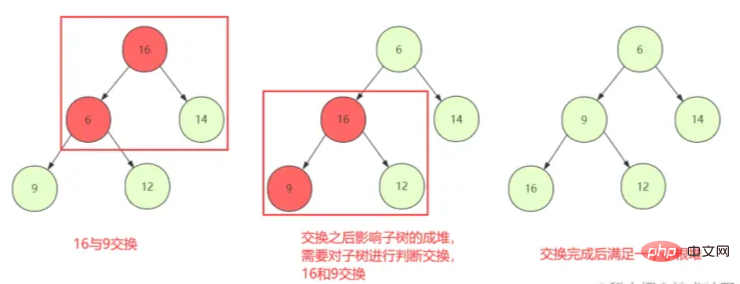
der Heap
-die Heap-Struktur zerstören.
① Setzen Sie also einfach das letzte Element an die erste Stelle. Auf diese Weise müssen Sie nur die Swap-Verschiebung (shiftDown) beurteilen, müssen jedoch beachten, dass sich zu diesem Zeitpunkt die Größe des gesamten Heaps geändert hat. Wir werden die verworfene Position logischerweise nicht verwenden, daher müssen wir einen Heap einschließen Größenparameter beim Entwerfen der Funktion.
② Wiederholen Sie den obigen Vorgang, bis alle Elemente im Heap erhalten sind.
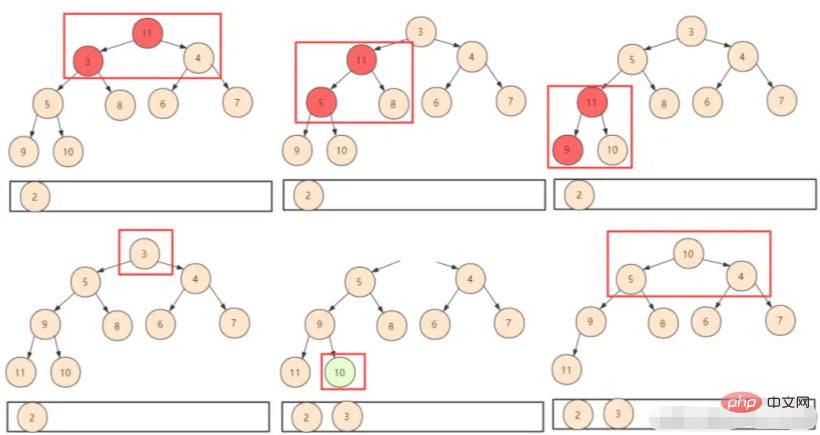
In Bezug auf die Analyse der Komplexität des Heap-Algorithmus betrug die Komplexität der vorherigen Heap-Erstellungszeit O (n). Jedes Mal, wenn der obere Teil des Heaps gelöscht und dann nach unten verschoben wird, wird die jeweilige Nummer protokolliert. Auf diese Weise beträgt die Komplexität O(nlogn) und die Gesamtzeitkomplexität beträgt O(n)+O(nlogn)=O(nlogn).
Heap eignet sich zur Aufrechterhaltung des maximalen Werts der Sammlung.
Nach dem Herausspringen eines Elements aus dem Heap sind die Kosten für eine erneute Anpassung zum Erhalten des obersten Elements des Heaps (dh des zweithöchsten Werts) relativ gering, da der Heap nach dem Herausspringen des Elements ein Halbwert ist -Fertigprodukt, und der zweithöchste Wert wird aus einem Halbzeug erhalten. Natürlich sind die Kosten relativ gering und die Zeitkomplexität beträgt O(logn), aber wenn es einmal durchlaufen wird, um den zweithöchsten Wert zu finden, Die Zeitkomplexität beträgt O(n).
ist in Javascript ES6 geschrieben.
Heap {
Konstruktor(Daten, Comp) {
this.data = data ? data : [];
// Vergleichsregeln: flexibler, Sie können Werte oder Objekte vergleichen this.compartor = comp ? comp : (ab) => ab;
// An Heap anpassen (Prioritätswarteschlange)
this.heapify();
}
heapify() {
if(this.size() <= 1) return;
// Beginnen Sie mit der Anpassung ab dem ersten Nicht-Blattknoten, oder Sie können die Anpassung ab dem letzten Element vornehmen for(let i=Math.floor((this.size()-2)/2); i>=0; i-- ) {
//Anpassen des Heaps kann auch durch Rekursion implementiert werden. Hier wird die Iteration verwendet, um this.shiftDown(i) zu implementieren.
}
}
// ShiftDown(i) nach unten anpassen {
let left = 2*i +1;
let right = 2*i +2;
let len = this.size();
while(i < len) {
let findIndex = i;
//Das linke Kind ist „größer“
if(left < len && this.compartor(this.data[left], this.data[findIndex]) < 0) {
findIndex = left;
}
// Das richtige Kind ist „größer“
if(right < len && this.compartor(this.data[right], this.data[findIndex]) < 0) {
findIndex = right;
}
if(i !== findIndex) {
//Den aktuellen Knoten gegen einen größeren Wert austauschen [this.data[i], this.data[findIndex]] = [this.data[findIndex], this.data[i]];
// Nach dem Anpassen dieser Ebene kann sich dies auf die Eigenschaften des Heaps der unteren Ebene auswirken. Passen Sie daher die untere Ebene weiter an (iterative Implementierung oder rekursiv).
i = findIndex;
links = 2*i +1;
rechts = 2*i +2;
}
anders {
// Wenn keine Anpassung erforderlich ist, springe heraus (muss herausspringen, sonst kann die Schleife nicht enden)
brechen;
}
}
}
// ShiftUp(i) nach oben anpassen
// Den Index des übergeordneten Elements finden let parentIndex = Math.floor((i-1)/2);
// Passen Sie das Maximum auf 0 an
while(parentIndex >=0 ) {
let findIndex = i;
if(this.compartor(this.data[parentIndex], this.data[findIndex]) > 0) {
findIndex = parentIndex;
}
if(findIndex !== i) {
[this.data[i], this.data[findIndex]] = [this.data[findIndex], this.data[i]];
i = findIndex;
parentIndex = Math.floor((i-1)/2);
}
anders {
brechen;
}
}
}
// Ermitteln Sie die Anzahl aller Elemente im Heap size(){
return this.data.length;
}
// Holen Sie sich das erste Element des Heaps peek(){
if(!this.size()) return null;
return this.data[0];
}
//Ein Element zum Heap hinzufügen push(x){
this.data.push(x);
this.shiftUp(this.data.length-1);
}
// Das erste Element aus dem Heap entfernen pop(){
if(!this.size()) return null;
let res = this.data[0];
if(this.size() == 1) {
this.data.pop();
}
anders {
this.data[0] = this.data[this.data.length-1];
this.data.length = this.data.length-1;
this.shiftDown(0);
}
res zurückgeben;
}
} let arr = [2,9,8,6,3,10,5,7,4,1];
sei comp = (a, b) => ab;
let heap = new Heap(arr, comp);
sei res = [];
while(heap.size()) {
res.push(heap.pop());
}
console.log(res); Das Element in arr kann auch ein Objekt sein.
Das Verzeichnis packets/scheduler im React-Quellcode ist der Code, der sich auf das Aufgabenplanungsmodul von React bezieht.
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src/Scheduler.js
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src /SchedulerMinHeap.js
/**
* Copyright (c) Facebook, Inc. und seine verbundenen Unternehmen.
*
* Dieser Quellcode ist unter der MIT-Lizenz lizenziert, die in der enthalten ist
* LICENSE-Datei im Stammverzeichnis dieses Quellbaums.
*
* @flow streng
*/
type Heap = Array<Node>;
Typ Node = {|
ID: Nummer,
sortIndex: Zahl,
|};
Exportfunktion push(heap: Heap, node: Node): void {
const index = heap.length;
heap.push(node);
siftUp(heap, node, index);
}
Exportfunktion peek(heap: Heap): Node |.
const first = heap[0];
return first === undefiniert ? null : first;
}
Exportfunktion pop(heap: Heap): Node |.
const first = heap[0];
if (first !== undefiniert) {
const last = heap.pop();
if (last !== first) {
heap[0] = last;
siftDown(heap, last, 0);
}
zuerst zurückkommen;
} anders {
null zurückgeben;
}
}
Funktion siftUp(heap, node, i) {
sei index = i;
while (wahr) {
const parentIndex = (index - 1) >>> 1;
const parent = heap[parentIndex];
if (parent !== undefiniert && Compare(parent, node) > 0) {
// Das übergeordnete Element ist größer.
heap[parentIndex] = node;
heap[index] = übergeordnetes Element;
index = parentIndex;
} anders {
// Das übergeordnete Element ist kleiner.
zurückkehren;
}
}
}
Funktion siftDown(heap, node, i) {
sei index = i;
const length = heap.length;
while (Index < Länge) {
const leftIndex = (index + 1) * 2 - 1;
const left = heap[leftIndex];
const rightIndex = leftIndex + 1;
const right = heap[rightIndex];
// Wenn der linke oder rechte Knoten kleiner ist, tausche ihn gegen den kleineren aus.
if (left !== undefiniert && Compare(left, node) < 0) {
if (right !== undefiniert && Compare(right, left) < 0) {
heap[index] = rechts;
heap[rightIndex] = node;
index = rightIndex;
} anders {
heap[index] = left;
heap[leftIndex] = node;
index = leftIndex;
}
} else if (right !== undefiniert && Compare(right, node) < 0) {
heap[index] = rechts;
heap[rightIndex] = node;
index = rightIndex;
} anders {
// Keines der Kinder ist kleiner.
zurückkehren;
}
}
}
Funktion vergleichen(a, b) {
// Zuerst den Sortierindex und dann die Aufgaben-ID vergleichen.
const diff = a.sortIndex - b.sortIndex;
return diff !== 0 ? diff : a.id - b.id;
} Der von uns implementierte minimale Heap unterscheidet sich geringfügig von der Implementierung in React, aber die Idee ist dieselbe, nur der Code ist anders geschrieben.
die Aufgabenplanung in React mithilfe des minimalen Heaps implementiert wird. Wenn wir zuvor ein gewisses Verständnis für den minimalen Heap haben, werden wir diesen Inhalt schneller lernen. Ich persönlich denke, wie wichtig es ist, Wissen in einem frühen Stadium anzusammeln, aber dieser Prozess kann langweilig sein. Glauben Sie, dass Sie zum jetzigen Zeitpunkt einige Algorithmen kennen? Tatsächlich handelt es sich dabei um Einsteigeralgorithmen, mit denen Sie noch nicht einmal begonnen haben. Denn im Aufgabenplanungsszenario von React sind die umzusetzenden Anforderungen sehr klar und auch die zu verwendenden Datenstrukturen und Algorithmen sind klar. In einigen tatsächlichen Szenarien kennen wir die spezifischen Anforderungen, wissen jedoch nicht, welche Datenergebnisse und Algorithmen wir verwenden sollen. Wir müssen die Anforderungen abstrahieren und spezifische Datenstrukturen und Algorithmen basierend auf dem abstrakten Datenmodell entwerfen . .