dsc 2 22 03 MLE gaussian lab bain trial jan19

MLE con Distribuciones Normales - Laboratorio

Introducción

En esta práctica de laboratorio, pondremos en práctica las fórmulas matemáticas que vimos en la lección anterior para ver cómo funciona MLE con distribuciones normales.

Objetivos

Podrás:

• Comprender y describir cómo funciona MLE con distribuciones normales.
• Ajustar una distribución normal a datos dados identificando la media y la varianza
• Compare visualmente la distribución ajustada con la distribución real

Nota: *En este sitio web se puede ver una derivación detallada de todas las ecuaciones MLE con pruebas. *

MLE en Python

Veamos a continuación un ejemplo de MLE y ajustes de distribución con Python. Aquí scipy.stats.norm.fit calcula los parámetros de distribución utilizando la estimación de máxima verosimilitud.

Importar bibliotecas necesarias

 from scipy . stats import norm # for generating sample data and fitting distributions
import matplotlib . pyplot as plt
plt . style . use ( 'seaborn' )
import numpy as np

Genere una matriz de 200 muestras aleatorias a partir de una dist normal con media 0 y stdv 1

 sample = None

Racor de distribución mediante MLE

- Utilice stats.norm.fit(data) para ajustar una distribución a los datos anteriores.

- Esto devuelve una lista de dos parámetros: (media: parámetros [0] y estándar: parámetros [1]) a través de un enfoque MLE

 param = None

#param[0], param[1]
# (0.08241224761452863, 1.002987490235812)

Calcule el PDF a partir de a) parámetros de datos reales b) parámetros ajustados con x = np.linspace(-5,5,100)

 x = np . linspace ( - 5 , 5 , 100 )

# Generate the pdf from fitted parameters (fitted distribution)
fitted_pdf = None
# Generate the pdf without fitting (normal distribution non fitted)
normal_pdf = None

Visualice ambos PDF

 # Your code here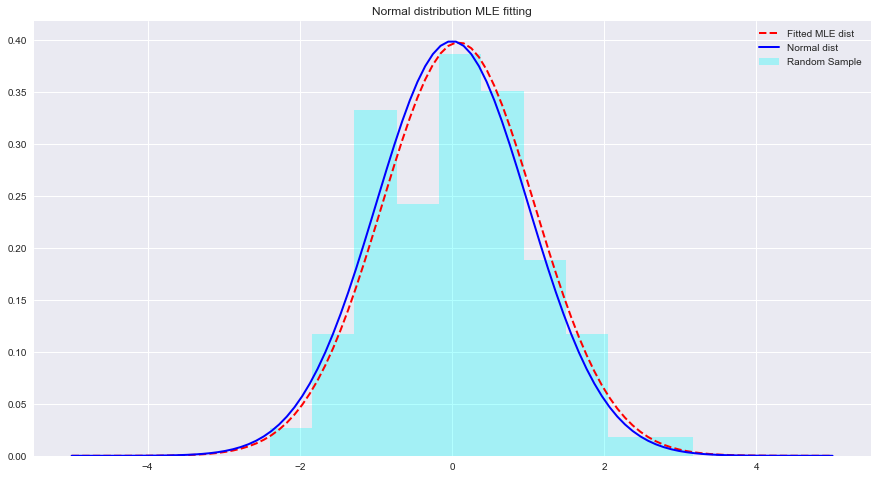 

 #  Your comments/observations 

Resumen

En esta breve práctica de laboratorio, analizamos la configuración bayesiana en un contexto gaussiano, es decir, cuando las variables aleatorias subyacentes se distribuyen normalmente. Aprendimos que MLE puede estimar los parámetros desconocidos de una distribución normal maximizando la probabilidad de la media esperada. La media esperada se acerca mucho a la media de una distribución normal no ajustada dentro de ese espacio de parámetros. Avanzaremos con esta comprensión para aprender cómo se realizan dichas estimaciones al estimar medias de varias clases presentes en la distribución de datos utilizando el Clasificador Naive Bayes.