

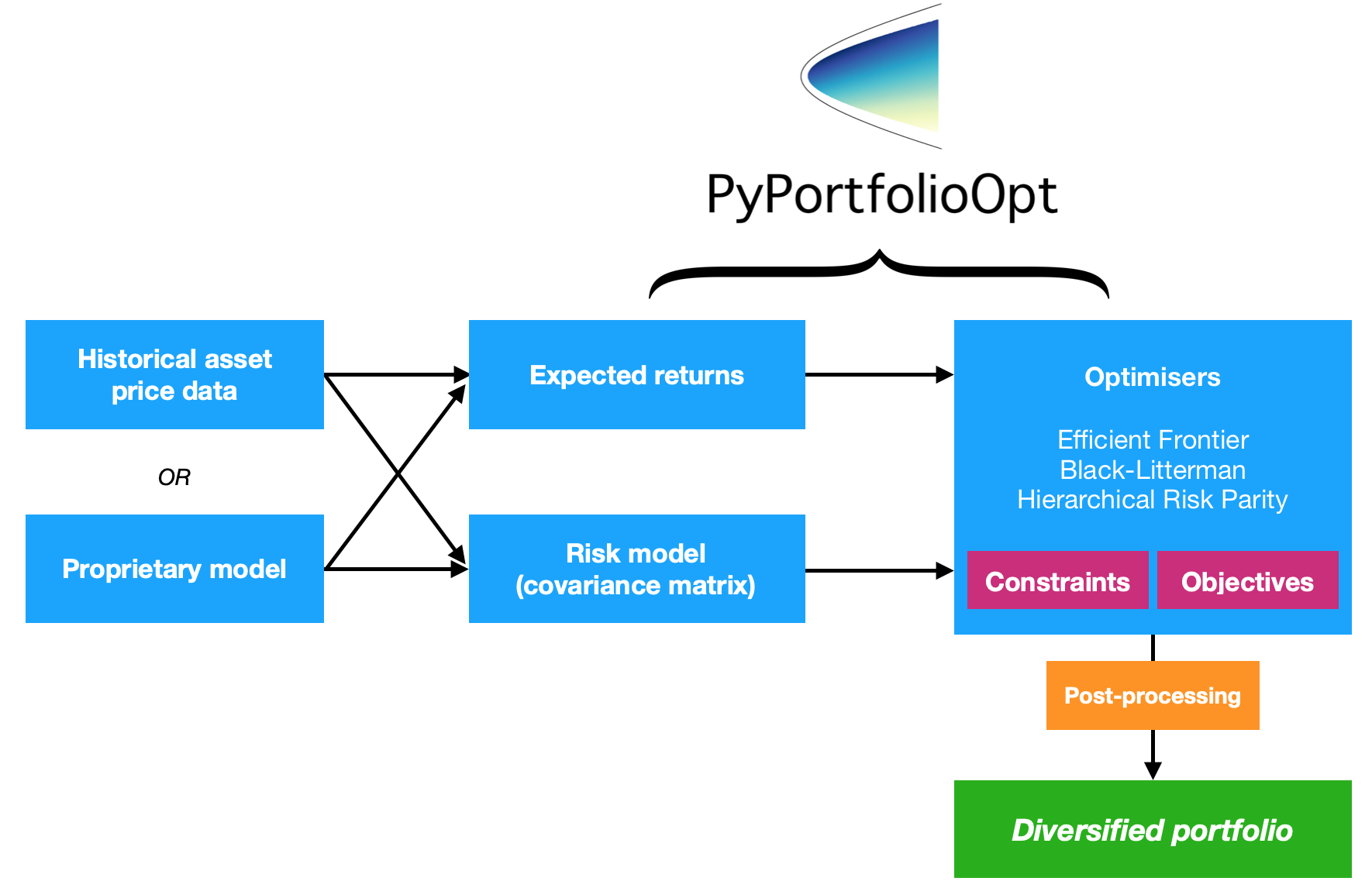
PyPortfolioOpt es una biblioteca que implementa métodos de optimización de cartera, incluidas técnicas clásicas de optimización de varianza media y asignación de Black-Litterman, así como desarrollos más recientes en el campo como la contracción y la paridad de riesgo jerárquico.
Es extenso pero fácilmente extensible y puede ser útil tanto para inversores ocasionales como para un profesional que busca una herramienta sencilla de creación de prototipos. Si usted es un inversor orientado a los fundamentos que ha identificado un puñado de opciones infravaloradas o un operador algorítmico que tiene una canasta de estrategias, PyPortfolioOpt puede ayudarlo a combinar sus fuentes alfa de una manera eficiente en cuanto al riesgo.
¿PyPortfolioOpt ha sido publicado en el Journal of Open Source Software?
Tuan Tran ahora mantiene PyPortfolioOpt.
Dirígete a la documentación en ReadTheDocs para ver en profundidad el proyecto, o consulta el libro de cocina para ver algunos ejemplos que muestran el proceso completo, desde la descarga de datos hasta la creación de un portafolio.
Si desea jugar con PyPortfolioOpt de forma interactiva en su navegador, puede iniciar Binder aquí. La configuración lleva un tiempo, pero le permite probar las recetas del libro de cocina sin tener que cumplir con todos los requisitos.
Nota: los usuarios de macOS deberán instalar herramientas de línea de comandos.
Nota: si estás en Windows, primero necesitas instalar C++. (descargar, instalar instrucciones)
Este proyecto está disponible en PyPI, lo que significa que puedes simplemente:
pip install PyPortfolioOpt(Es posible que deba seguir instrucciones de instalación independientes para cvxopt y cvxpy).
Sin embargo, se recomienda utilizar un administrador de dependencias dentro de un entorno virtual. Mi recomendación actual es que te prepares con poesía y luego simplemente ejecutes
poetry add PyPortfolioOptDe lo contrario, clone/descargue el proyecto y en el directorio del proyecto ejecute:
python setup.py install PyPortfolioOpt es compatible con Docker. Construya su primer contenedor con docker build -f docker/Dockerfile . -t pypfopt . Puede utilizar la imagen para ejecutar pruebas o incluso iniciar un servidor Jupyter.
# iPython interpreter:
docker run -it pypfopt poetry run ipython
# Jupyter notebook server:
docker run -it -p 8888:8888 pypfopt poetry run jupyter notebook --allow-root --no-browser --ip 0.0.0.0
# click on http://127.0.0.1:8888/?token=xxx
# Pytest
docker run -t pypfopt poetry run pytest
# Bash
docker run -it pypfopt bashPara obtener más información, lea esta guía.
Si desea realizar cambios importantes para integrarlo con su sistema propietario, probablemente tenga sentido clonar este repositorio y utilizar sólo el código fuente.
git clone https://github.com/robertmartin8/PyPortfolioOptAlternativamente, puedes intentar:
pip install -e git+https://github.com/robertmartin8/PyPortfolioOpt.gitA continuación se muestra un ejemplo de datos bursátiles de la vida real, que demuestra lo fácil que es encontrar la cartera a largo plazo que maximice el índice de Sharpe (una medida de los rendimientos ajustados al riesgo).
import pandas as pd
from pypfopt import EfficientFrontier
from pypfopt import risk_models
from pypfopt import expected_returns
# Read in price data
df = pd . read_csv ( "tests/resources/stock_prices.csv" , parse_dates = True , index_col = "date" )
# Calculate expected returns and sample covariance
mu = expected_returns . mean_historical_return ( df )
S = risk_models . sample_cov ( df )
# Optimize for maximal Sharpe ratio
ef = EfficientFrontier ( mu , S )
raw_weights = ef . max_sharpe ()
cleaned_weights = ef . clean_weights ()
ef . save_weights_to_file ( "weights.csv" ) # saves to file
print ( cleaned_weights )
ef . portfolio_performance ( verbose = True )Esto genera los siguientes pesos:
{'GOOG': 0.03835,
'AAPL': 0.0689,
'FB': 0.20603,
'BABA': 0.07315,
'AMZN': 0.04033,
'GE': 0.0,
'AMD': 0.0,
'WMT': 0.0,
'BAC': 0.0,
'GM': 0.0,
'T': 0.0,
'UAA': 0.0,
'SHLD': 0.0,
'XOM': 0.0,
'RRC': 0.0,
'BBY': 0.01324,
'MA': 0.35349,
'PFE': 0.1957,
'JPM': 0.0,
'SBUX': 0.01082}
Expected annual return: 30.5%
Annual volatility: 22.2%
Sharpe Ratio: 1.28Esto es interesante pero no útil en sí mismo. Sin embargo, PyPortfolioOpt proporciona un método que le permite convertir las ponderaciones continuas anteriores en una asignación real que podría comprar. Simplemente ingrese los precios más recientes y el tamaño de cartera deseado ($10,000 en este ejemplo):
from pypfopt . discrete_allocation import DiscreteAllocation , get_latest_prices
latest_prices = get_latest_prices ( df )
da = DiscreteAllocation ( weights , latest_prices , total_portfolio_value = 10000 )
allocation , leftover = da . greedy_portfolio ()
print ( "Discrete allocation:" , allocation )
print ( "Funds remaining: ${:.2f}" . format ( leftover ))12 out of 20 tickers were removed
Discrete allocation: {'GOOG': 1, 'AAPL': 4, 'FB': 12, 'BABA': 4, 'BBY': 2,
'MA': 20, 'PFE': 54, 'SBUX': 1}
Funds remaining: $ 11.89Descargo de responsabilidad: nada sobre este proyecto constituye un consejo de inversión y el autor no asume ninguna responsabilidad por sus decisiones de inversión posteriores. Consulte la licencia para obtener más información.
El artículo de Harry Markowitz de 1952 es un clásico innegable, que convirtió la optimización de carteras de un arte a una ciencia. La idea clave es que al combinar activos con diferentes rendimientos y volatilidades esperadas, se puede decidir una asignación matemáticamente óptima que minimice el riesgo de un rendimiento objetivo; el conjunto de todas esas carteras óptimas se denomina frontera eficiente .
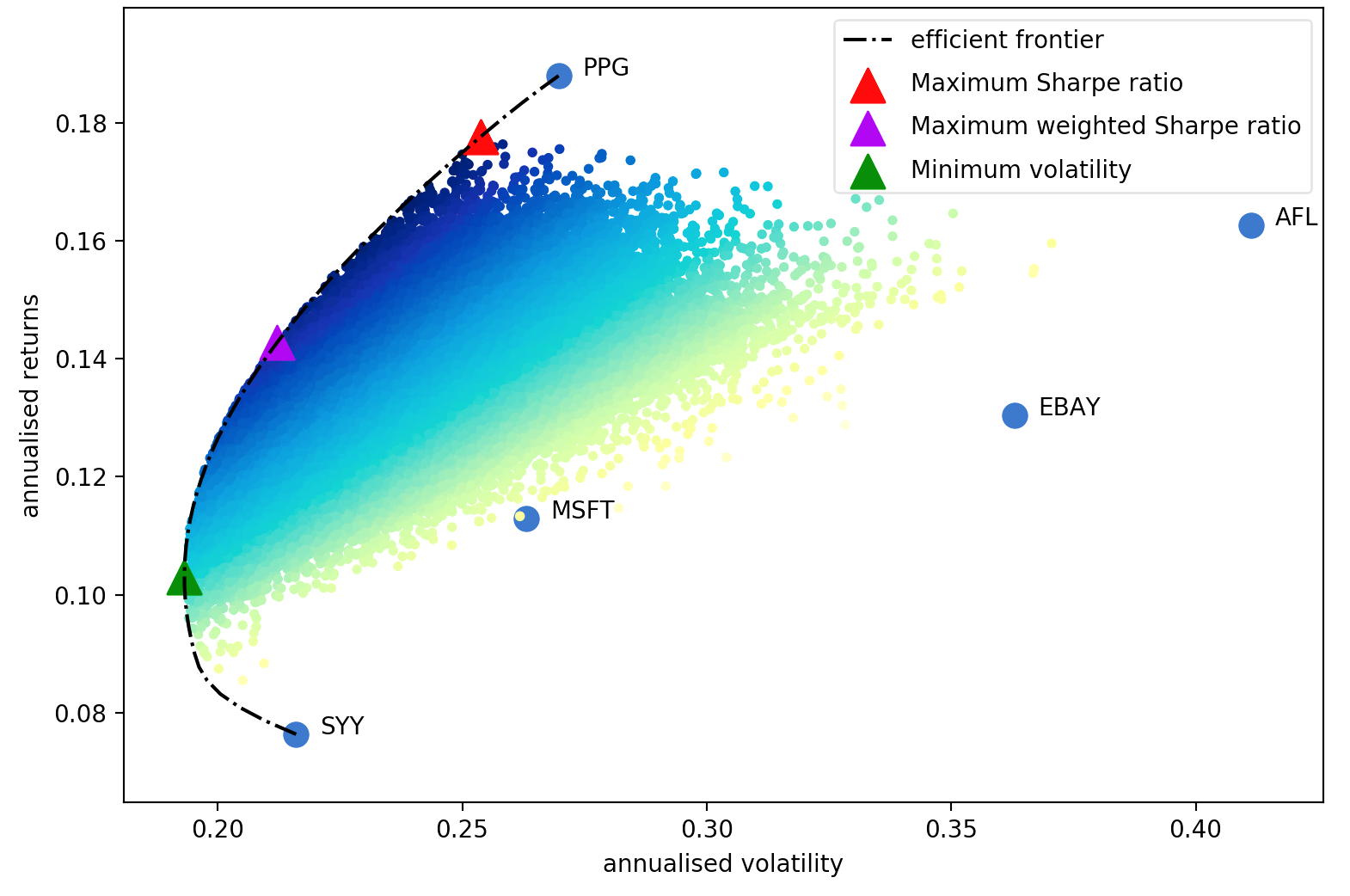
Aunque se ha avanzado mucho en el tema, más de medio siglo después, las ideas centrales de Markowitz siguen siendo de fundamental importancia y se utilizan a diario en muchas empresas de gestión de carteras. El principal inconveniente de la optimización de la varianza media es que el tratamiento teórico requiere conocimiento de los rendimientos esperados y las características de riesgo futuras (covarianza) de los activos. Obviamente, si supiéramos que los rendimientos esperados de las acciones serían mucho más fáciles, pero todo el juego es que los rendimientos de las acciones son notoriamente difíciles de pronosticar. Como sustituto, podemos derivar estimaciones del rendimiento esperado y la covarianza basadas en datos históricos; aunque perdemos las garantías teóricas proporcionadas por Markowitz, cuanto más se acerquen nuestras estimaciones a los valores reales, mejor será nuestra cartera.
Por lo tanto, este proyecto proporciona cuatro conjuntos principales de funcionalidades (aunque, por supuesto, están íntimamente relacionadas)
Un objetivo de diseño clave de PyPortfolioOpt es la modularidad : el usuario debería poder intercambiar sus componentes sin dejar de utilizar el marco que proporciona PyPortfolioOpt.
En esta sección, detallamos algunas de las funciones disponibles de PyPortfolioOpt. Se ofrecen más ejemplos en los cuadernos de Jupyter aquí. Otro buen recurso son los tests.
Puede encontrar una versión mucho más completa de esto en ReadTheDocs, así como posibles extensiones para usuarios más avanzados.
La matriz de covarianza codifica no sólo la volatilidad de un activo, sino también cómo se correlaciona con otros activos. Esto es importante porque para aprovechar los beneficios de la diversificación (y así aumentar el rendimiento por unidad de riesgo), los activos de la cartera deben estar lo menos correlacionados posible.
sklearn.covariance .constant_variance , single_factor y constant_correlation .sklearn.covariance 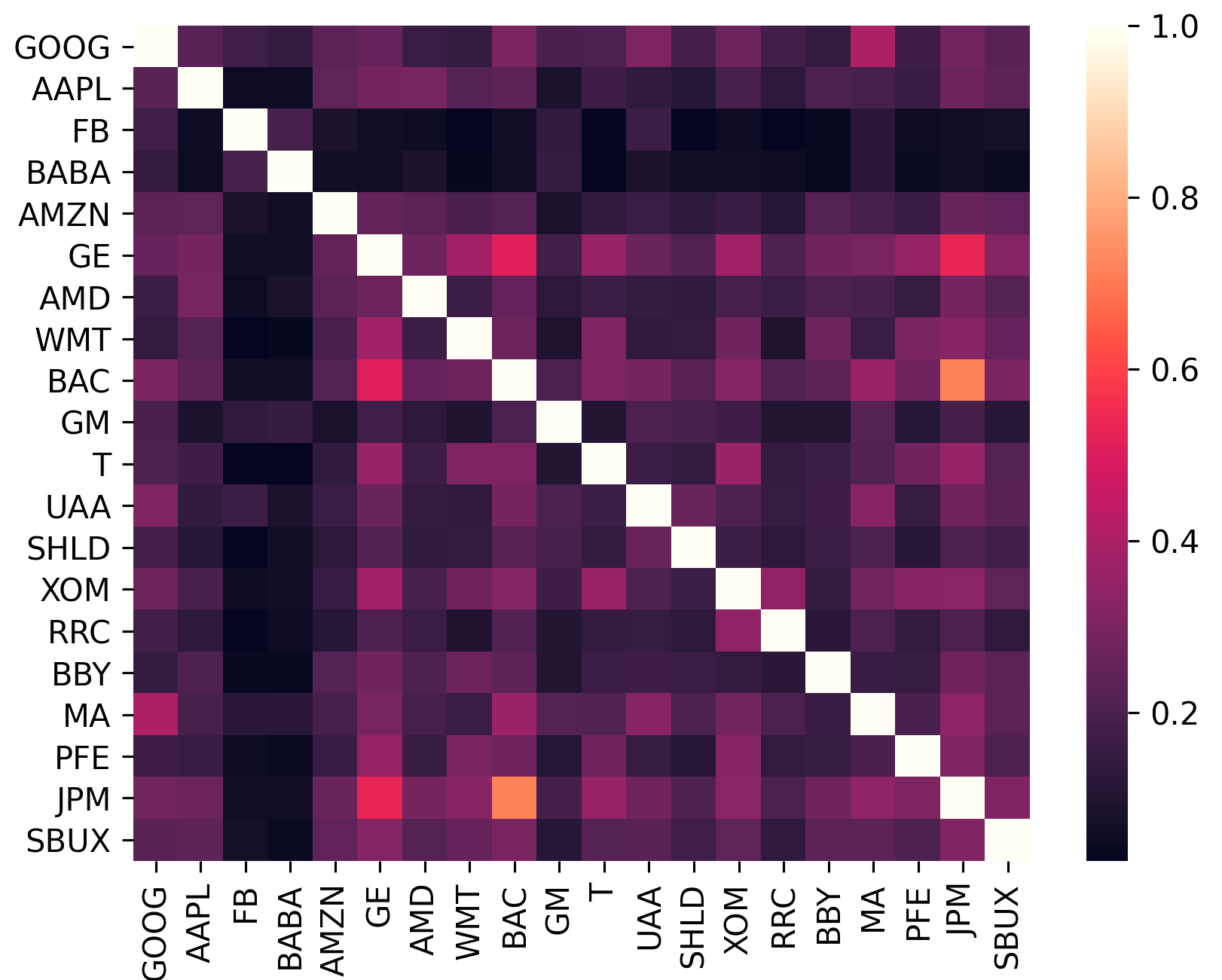
(Este gráfico se generó usando plotting.plot_covariance )
ef = EfficientFrontier ( mu , S , weight_bounds = ( - 1 , 1 ))efficient_risk y efficient_return , PyPortfolioOpt ofrece una opción para formar una cartera neutral al mercado (es decir, las ponderaciones suman cero). Esto no es posible para la cartera máxima de Sharpe y la cartera de volatilidad mínima porque en esos casos no son invariantes con respecto al apalancamiento. La neutralidad del mercado requiere ponderaciones negativas: ef = EfficientFrontier ( mu , S , weight_bounds = ( - 1 , 1 ))
ef . efficient_return ( target_return = 0.2 , market_neutral = True ) ef = EfficientFrontier ( mu , S , weight_bounds = ( 0 , 0.1 )) Un problema con la optimización de media-varianza es que conduce a muchas ponderaciones cero. Si bien estos son "óptimos" dentro de la muestra, hay una gran cantidad de investigaciones que muestran que esta característica hace que las carteras de varianza media tengan un rendimiento inferior fuera de la muestra. Con ese fin, he introducido una función objetivo que puede reducir el número de pesos insignificantes para cualquiera de las funciones objetivo. Esencialmente, agrega una penalización (parametrizada por gamma ) en pesos pequeños, con un término que se parece a la regularización L2 en el aprendizaje automático. Puede que sea necesario probar varios valores gamma para lograr el número deseado de pesos no despreciables. Para la cartera de prueba de 20 valores, gamma ~ 1 es suficiente
ef = EfficientFrontier ( mu , S )
ef . add_objective ( objective_functions . L2_reg , gamma = 1 )
ef . max_sharpe ()A partir de la versión 0.5.0, ahora admitimos la asignación de activos de Black-Litterman, que le permite combinar una estimación previa de los rendimientos (por ejemplo, los rendimientos implícitos en el mercado) con sus propios puntos de vista para formar una estimación posterior. Esto da como resultado estimaciones mucho mejores de los rendimientos esperados que simplemente utilizar el rendimiento histórico medio. Consulte los documentos para obtener una discusión sobre la teoría, así como consejos sobre el formato de las entradas.
S = risk_models . sample_cov ( df )
viewdict = { "AAPL" : 0.20 , "BBY" : - 0.30 , "BAC" : 0 , "SBUX" : - 0.2 , "T" : 0.131321 }
bl = BlackLittermanModel ( S , pi = "equal" , absolute_views = viewdict , omega = "default" )
rets = bl . bl_returns ()
ef = EfficientFrontier ( rets , S )
ef . max_sharpe () Las características anteriores se refieren principalmente a la resolución de problemas de optimización de varianza media mediante programación cuadrática (aunque cvxpy se encarga de esto). Sin embargo, también ofrecemos diferentes optimizadores:
Consulte la documentación para obtener más información.
Las pruebas están escritas en pytest (en mi opinión, mucho más intuitivas que unittest y sus variantes) y he tratado de garantizar una cobertura cercana al 100%. Ejecute las pruebas navegando al directorio del paquete y simplemente ejecutando pytest en la línea de comando.
PyPortfolioOpt proporciona un conjunto de datos de prueba de rendimientos diarios para 20 tickers:
[ 'GOOG' , 'AAPL' , 'FB' , 'BABA' , 'AMZN' , 'GE' , 'AMD' , 'WMT' , 'BAC' , 'GM' ,
'T' , 'UAA' , 'SHLD' , 'XOM' , 'RRC' , 'BBY' , 'MA' , 'PFE' , 'JPM' , 'SBUX' ]Estos tickers han sido seleccionados informalmente para cumplir con varios criterios:
Actualmente, las pruebas no han explorado todos los casos extremos y combinaciones de funciones y parámetros objetivos. Sin embargo, cada método y parámetro ha sido probado para que funcione según lo previsto.
Si utiliza PyPortfolioOpt para trabajos publicados, cite el artículo JOSS.
Cadena de citas:
Martin, R. A., (2021). PyPortfolioOpt: portfolio optimization in Python. Journal of Open Source Software, 6(61), 3066, https://doi.org/10.21105/joss.03066
BibTex::
@article { Martin2021 ,
doi = { 10.21105/joss.03066 } ,
url = { https://doi.org/10.21105/joss.03066 } ,
year = { 2021 } ,
publisher = { The Open Journal } ,
volume = { 6 } ,
number = { 61 } ,
pages = { 3066 } ,
author = { Robert Andrew Martin } ,
title = { PyPortfolioOpt: portfolio optimization in Python } ,
journal = { Journal of Open Source Software }
}Las contribuciones son muy bienvenidas . Eche un vistazo a la Guía de contribuciones para obtener más información.
Me gustaría agradecer a todas las personas que han contribuido a PyPortfolioOpt desde su lanzamiento en 2018. Un agradecimiento especial a: