ai simplest network
1.0.0
Esta es la red neuronal artificial más simple posible explicada y demostrada.
Las redes neuronales artificiales se inspiran en el cerebro al tener neuronas artificiales interconectadas que almacenan patrones y se comunican entre sí. La forma más simple de una neurona artificial tiene una o múltiples entradas. 
cada uno tiene un peso específico 
y una salida 
.
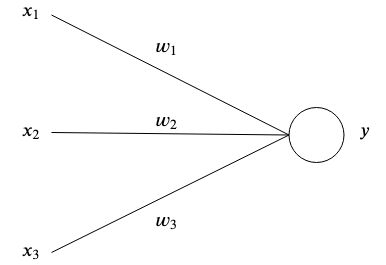
En el nivel más simple, la salida es la suma de sus entradas multiplicada por sus pesos.
El propósito de una red es aprender una determinada salida. dadas ciertas entradas 
aproximando una función compleja con muchos parámetros 
que no pudimos lograrlo nosotros mismos.
Digamos que tenemos una red con dos entradas. 
y 
y dos pesas 
y 
.
La idea es ajustar los pesos de tal manera que las entradas dadas produzcan el resultado deseado.
Los pesos normalmente se inicializan aleatoriamente ya que no podemos conocer su valor óptimo de antemano; sin embargo, para simplificar, los inicializaremos a ambos para 
.
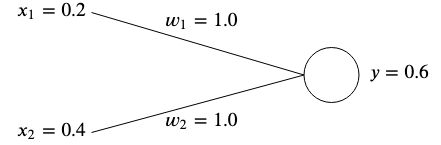
Si calculamos la salida de esta red, obtendremos
Si la salida no coincide con el valor objetivo esperado, entonces tenemos un error.
Por ejemplo, si quisiéramos obtener un valor objetivo de 
Entonces tendríamos una diferencia de
Una forma común de medir el error (también conocida como función de costo) es utilizar el error cuadrático medio:
Si tuviéramos múltiples asociaciones de entradas y valores objetivo, entonces el error se convierte en la suma promedio de cada asociación.
Usamos el error cuadrático medio para medir qué tan lejos están los resultados de nuestro objetivo deseado. La cuadratura elimina los signos negativos y da más peso a las diferencias más grandes entre la producción y la meta.
Para rectificar el error, necesitaríamos ajustar los pesos de manera que la salida coincida con nuestro objetivo. En nuestro ejemplo, bajando de 
a 
funcionaría, ya que
Sin embargo, para ajustar los pesos de nuestras redes neuronales para muchas entradas y valores objetivo diferentes, necesitamos un algoritmo de aprendizaje que lo haga automáticamente.
La idea es utilizar el error para comprender cómo se debe ajustar cada peso para minimizar el error, pero primero debemos aprender sobre los gradientes.
Es esencialmente un vector que apunta a la dirección del ascenso más pronunciado de una función. El gradiente se denota con 
y es simplemente la derivada parcial de cada variable de una función expresada como un vector.
Se ve así para una función de dos variables:
Inyectemos algunos números y calculemos el gradiente con un ejemplo simple. Digamos que tenemos una función 
, entonces el gradiente sería
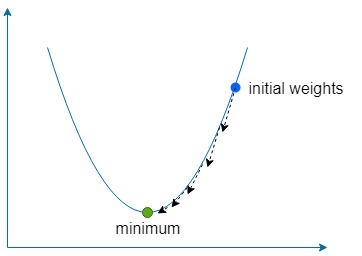
La parte de descenso simplemente significa usar el gradiente para encontrar la dirección del ascenso más pronunciado de nuestra función y luego ir en la dirección opuesta una pequeña cantidad muchas veces para encontrar el mínimo global (o a veces local) de la función.
Usamos una constante llamada tasa de aprendizaje , denotada con 
para definir qué pequeño paso dar en esa dirección.
Si es demasiado grande, entonces corremos el riesgo de sobrepasar el mínimo de la función, pero si es demasiado bajo, la red tardará más en aprender y corremos el riesgo de quedarnos atrapados en un mínimo local poco profundo.
Para nuestros dos pesos y Necesitamos encontrar el gradiente de esos pesos con respecto a la función de error. 
para ambos y , podemos encontrar el gradiente usando la regla de la cadena
De ahora en adelante denotaremos el 
como el 
término por simplicidad.
Una vez que tenemos el gradiente, podemos actualizar nuestros pesos restando el gradiente calculado multiplicado por la tasa de aprendizaje.
Y repetimos este proceso hasta que el error se minimice y se acerque lo suficiente a cero.
El ejemplo incluido enseña el siguiente conjunto de datos a una red neuronal con dos entradas y una salida mediante descenso de gradiente:
Una vez aprendido, la red debería generar ~0 cuando se le dan dos s y ~ cuando se le da un y un 
.
docker build -t simplest-network .
docker run --rm simplest-network
