dsc 2 22 03 MLE gaussian lab bain trial jan19

MLE avec distributions normales - Laboratoire

Introduction

Dans ce laboratoire, nous mettrons en pratique les formules mathématiques que nous avons vues dans la leçon précédente pour voir comment MLE fonctionne avec des distributions normales.

Objectifs

Vous pourrez :

• Comprendre et décrire comment MLE fonctionne avec les distributions normales
• Ajuster une distribution normale à des données données en identifiant la moyenne et la variance
• Comparez visuellement la distribution ajustée par rapport à la distribution réelle

Remarque : *Une dérivation détaillée de toutes les équations MLE avec preuves peut être consultée sur ce site Web. *

MLE en Python

Voyons ci-dessous un exemple de raccords MLE et de distribution avec Python. Ici, scipy.stats.norm.fit calcule les paramètres de distribution à l'aide de l'estimation du maximum de vraisemblance.

Importer les bibliothèques nécessaires

 from scipy . stats import norm # for generating sample data and fitting distributions
import matplotlib . pyplot as plt
plt . style . use ( 'seaborn' )
import numpy as np

Générer un tableau de 200 échantillons aléatoires à partir d'une distribution normale avec une moyenne de 0 et stdv 1

 sample = None

Montage de distribution via MLE

- Utilisez stats.norm.fit(data) pour ajuster une distribution aux données ci-dessus.

- Ceci renvoie une liste de deux paramètres : (mean,: settings[0] et std: settings[1]) via une approche MLE

 param = None

#param[0], param[1]
# (0.08241224761452863, 1.002987490235812)

Calculez le PDF à partir de a) les paramètres de données réels b) les paramètres ajustés avec x = np.linspace(-5,5,100)

 x = np . linspace ( - 5 , 5 , 100 )

# Generate the pdf from fitted parameters (fitted distribution)
fitted_pdf = None
# Generate the pdf without fitting (normal distribution non fitted)
normal_pdf = None

Visualisez les deux PDF

 # Your code here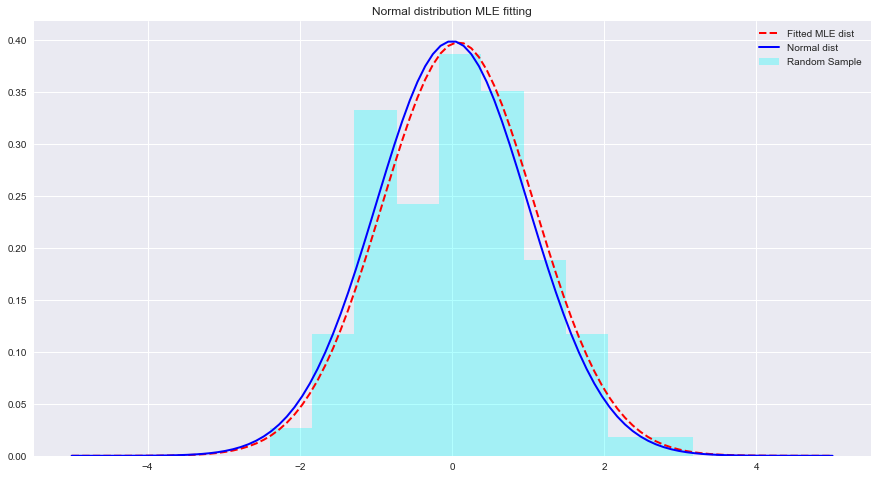 

 #  Your comments/observations 

Résumé

Dans ce court laboratoire, nous avons examiné le contexte bayésien dans un contexte gaussien, c'est-à-dire lorsque les variables aléatoires sous-jacentes sont normalement distribuées. Nous avons appris que MLE peut estimer les paramètres inconnus d'une distribution normale, en maximisant la probabilité de la moyenne attendue. La moyenne attendue est très proche de la moyenne d'une distribution normale non ajustée dans cet espace de paramètres. Nous allons poursuivre cette compréhension en apprenant comment de telles estimations sont effectuées pour estimer les moyennes d'un certain nombre de classes présentes dans la distribution de données à l'aide du classificateur Naive Bayes.