

PyPortfolioOpt est une bibliothèque qui implémente des méthodes d'optimisation de portefeuille, y compris les techniques classiques d'optimisation de la variance moyenne et l'allocation Black-Litterman, ainsi que des développements plus récents dans le domaine comme le rétrécissement et la parité des risques hiérarchiques.
Il est complet mais facilement extensible et peut être utile soit aux investisseurs occasionnels, soit aux professionnels à la recherche d'un outil de prototypage simple. Que vous soyez un investisseur axé sur les fondamentaux qui a identifié une poignée de choix sous-évalués ou un trader algorithmique disposant d'un panier de stratégies, PyPortfolioOpt peut vous aider à combiner vos sources d'alpha de manière efficace en termes de risque.
PyPortfolioOpt a été publié dans le Journal of Open Source Software ?
PyPortfolioOpt est désormais maintenu par Tuan Tran.
Rendez-vous sur la documentation sur ReadTheDocs pour obtenir un aperçu approfondi du projet, ou consultez le livre de recettes pour voir quelques exemples illustrant le processus complet, du téléchargement des données à la création d'un portefeuille.
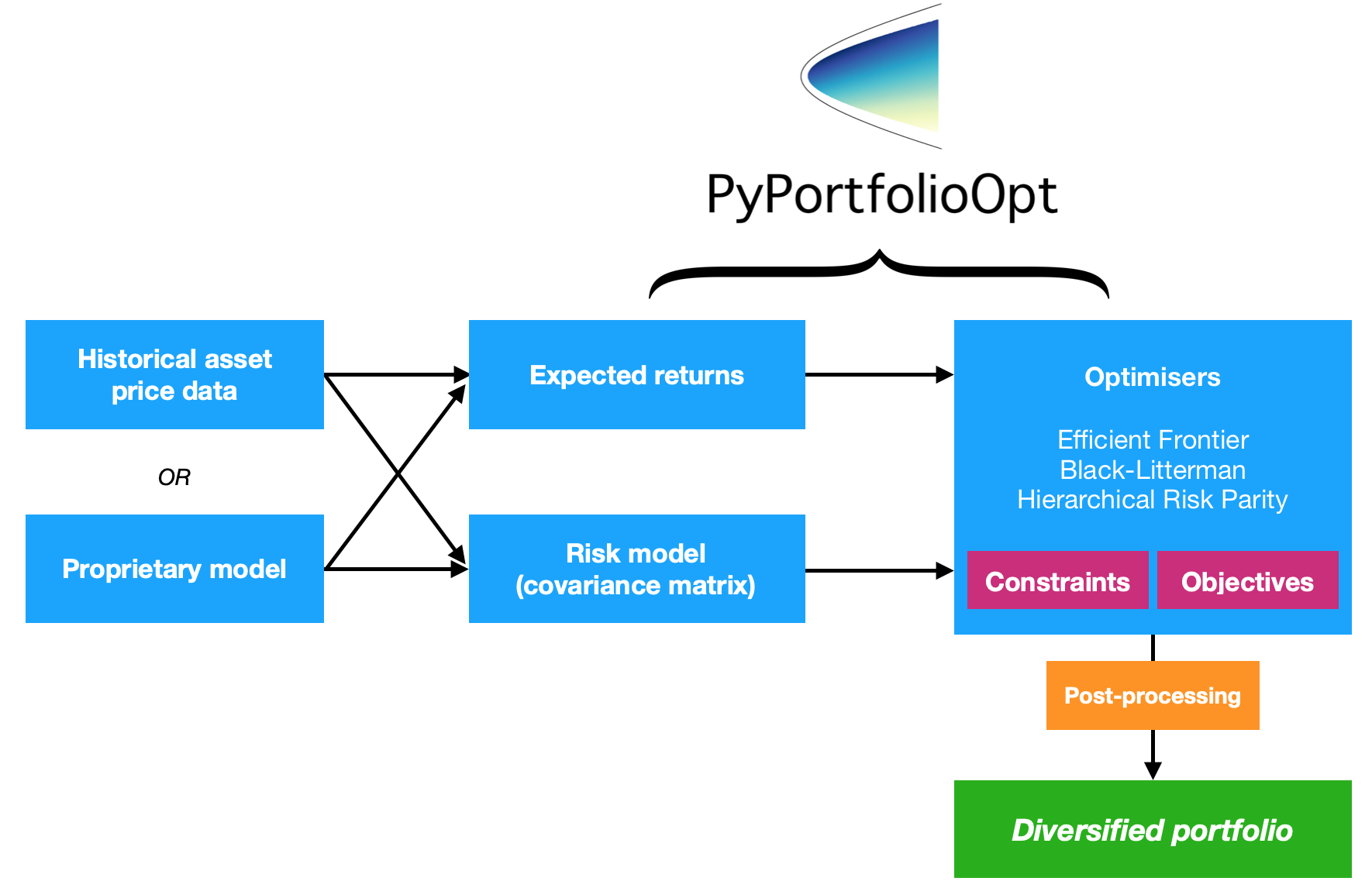
Si vous souhaitez jouer avec PyPortfolioOpt de manière interactive dans votre navigateur, vous pouvez lancer Binder ici. La configuration prend un certain temps, mais cela vous permet d'essayer les recettes du livre de recettes sans avoir à répondre à toutes les exigences.
Remarque : les utilisateurs de macOS devront installer les outils de ligne de commande.
Remarque : si vous êtes sous Windows, vous devez d'abord installer C++. (télécharger, instructions d'installation)
Ce projet est disponible sur PyPI, ce qui signifie que vous pouvez simplement :
pip install PyPortfolioOpt(vous devrez peut-être suivre des instructions d'installation distinctes pour cvxopt et cvxpy).
Cependant, il est préférable d'utiliser un gestionnaire de dépendances dans un environnement virtuel. Ma recommandation actuelle est de vous familiariser avec la poésie, puis de courir
poetry add PyPortfolioOptSinon, clonez/téléchargez le projet et dans le répertoire du projet exécutez :
python setup.py install PyPortfolioOpt prend en charge Docker. Créez votre premier conteneur avec docker build -f docker/Dockerfile . -t pypfopt . Vous pouvez utiliser l'image pour exécuter des tests ou même lancer un serveur Jupyter.
# iPython interpreter:
docker run -it pypfopt poetry run ipython
# Jupyter notebook server:
docker run -it -p 8888:8888 pypfopt poetry run jupyter notebook --allow-root --no-browser --ip 0.0.0.0
# click on http://127.0.0.1:8888/?token=xxx
# Pytest
docker run -t pypfopt poetry run pytest
# Bash
docker run -it pypfopt bashPour plus d’informations, veuillez lire ce guide.
Si vous souhaitez apporter des modifications majeures pour l'intégrer à votre système propriétaire, il est probablement logique de cloner ce référentiel et d'utiliser uniquement le code source.
git clone https://github.com/robertmartin8/PyPortfolioOptAlternativement, vous pouvez essayer :
pip install -e git+https://github.com/robertmartin8/PyPortfolioOpt.gitVoici un exemple basé sur des données boursières réelles, démontrant à quel point il est facile de trouver le portefeuille long-only qui maximise le ratio de Sharpe (une mesure des rendements ajustés au risque).
import pandas as pd
from pypfopt import EfficientFrontier
from pypfopt import risk_models
from pypfopt import expected_returns
# Read in price data
df = pd . read_csv ( "tests/resources/stock_prices.csv" , parse_dates = True , index_col = "date" )
# Calculate expected returns and sample covariance
mu = expected_returns . mean_historical_return ( df )
S = risk_models . sample_cov ( df )
# Optimize for maximal Sharpe ratio
ef = EfficientFrontier ( mu , S )
raw_weights = ef . max_sharpe ()
cleaned_weights = ef . clean_weights ()
ef . save_weights_to_file ( "weights.csv" ) # saves to file
print ( cleaned_weights )
ef . portfolio_performance ( verbose = True )Cela génère les poids suivants :
{'GOOG': 0.03835,
'AAPL': 0.0689,
'FB': 0.20603,
'BABA': 0.07315,
'AMZN': 0.04033,
'GE': 0.0,
'AMD': 0.0,
'WMT': 0.0,
'BAC': 0.0,
'GM': 0.0,
'T': 0.0,
'UAA': 0.0,
'SHLD': 0.0,
'XOM': 0.0,
'RRC': 0.0,
'BBY': 0.01324,
'MA': 0.35349,
'PFE': 0.1957,
'JPM': 0.0,
'SBUX': 0.01082}
Expected annual return: 30.5%
Annual volatility: 22.2%
Sharpe Ratio: 1.28C’est intéressant mais pas utile en soi. Cependant, PyPortfolioOpt fournit une méthode qui vous permet de convertir les pondérations continues ci-dessus en une allocation réelle que vous pourriez acheter. Entrez simplement les prix les plus récents et la taille de portefeuille souhaitée (10 000 $ dans cet exemple) :
from pypfopt . discrete_allocation import DiscreteAllocation , get_latest_prices
latest_prices = get_latest_prices ( df )
da = DiscreteAllocation ( weights , latest_prices , total_portfolio_value = 10000 )
allocation , leftover = da . greedy_portfolio ()
print ( "Discrete allocation:" , allocation )
print ( "Funds remaining: ${:.2f}" . format ( leftover ))12 out of 20 tickers were removed
Discrete allocation: {'GOOG': 1, 'AAPL': 4, 'FB': 12, 'BABA': 4, 'BBY': 2,
'MA': 20, 'PFE': 54, 'SBUX': 1}
Funds remaining: $ 11.89Avertissement : rien dans ce projet ne constitue un conseil en investissement et l'auteur n'assume aucune responsabilité pour vos décisions d'investissement ultérieures. Veuillez vous référer à la licence pour plus d'informations.
L'article de Harry Markowitz de 1952 est le classique indéniable qui a fait de l'optimisation de portefeuille un art en une science. L’idée clé est qu’en combinant des actifs avec des rendements et des volatilités attendus différents, on peut décider d’une allocation mathématiquement optimale qui minimise le risque pour un rendement cible – l’ensemble de tous ces portefeuilles optimaux est appelé frontière efficace .
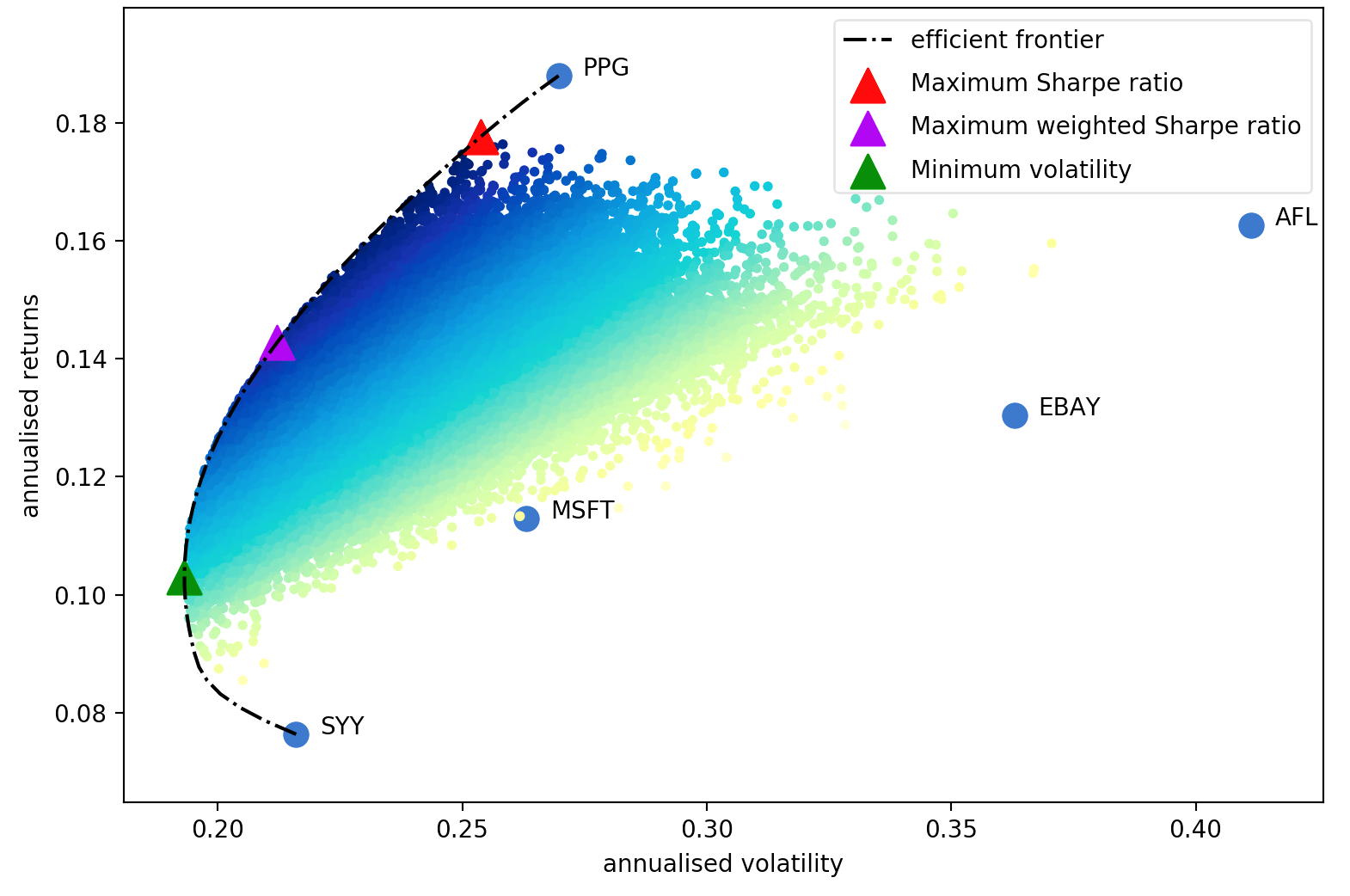
Bien que le sujet ait beaucoup évolué, plus d'un demi-siècle plus tard, les idées fondamentales de Markowitz restent fondamentales et sont utilisées quotidiennement dans de nombreuses sociétés de gestion de portefeuille. Le principal inconvénient de l’optimisation moyenne-variance est que le traitement théorique nécessite la connaissance des rendements attendus et des caractéristiques de risque futures (covariance) des actifs. Évidemment, si nous connaissions les rendements attendus d’une action, ce serait beaucoup plus facile, mais le problème est que les rendements boursiers sont notoirement difficiles à prévoir. Au lieu de cela, nous pouvons dériver des estimations du rendement attendu et de la covariance sur la base de données historiques – même si nous perdons les garanties théoriques fournies par Markowitz, plus nos estimations sont proches des valeurs réelles, meilleur sera notre portefeuille.
Ainsi, ce projet fournit quatre ensembles majeurs de fonctionnalités (bien qu'elles soient bien sûr intimement liées)
L'un des objectifs clés de la conception de PyPortfolioOpt est la modularité : l'utilisateur doit pouvoir échanger ses composants tout en continuant à utiliser le cadre fourni par PyPortfolioOpt.
Dans cette section, nous détaillons certaines des fonctionnalités disponibles de PyPortfolioOpt. D'autres exemples sont proposés dans les notebooks Jupyter ici. Les tests sont une autre bonne ressource.
Une version beaucoup plus complète de celui-ci peut être trouvée sur ReadTheDocs, ainsi que des extensions possibles pour les utilisateurs plus avancés.
La matrice de covariance code non seulement la volatilité d'un actif, mais également sa corrélation avec d'autres actifs. Ceci est important car pour bénéficier des avantages de la diversification (et ainsi augmenter le rendement par unité de risque), les actifs du portefeuille doivent être aussi décorrélés que possible.
sklearn.covariance .constant_variance , single_factor et constant_correlation .sklearn.covariance 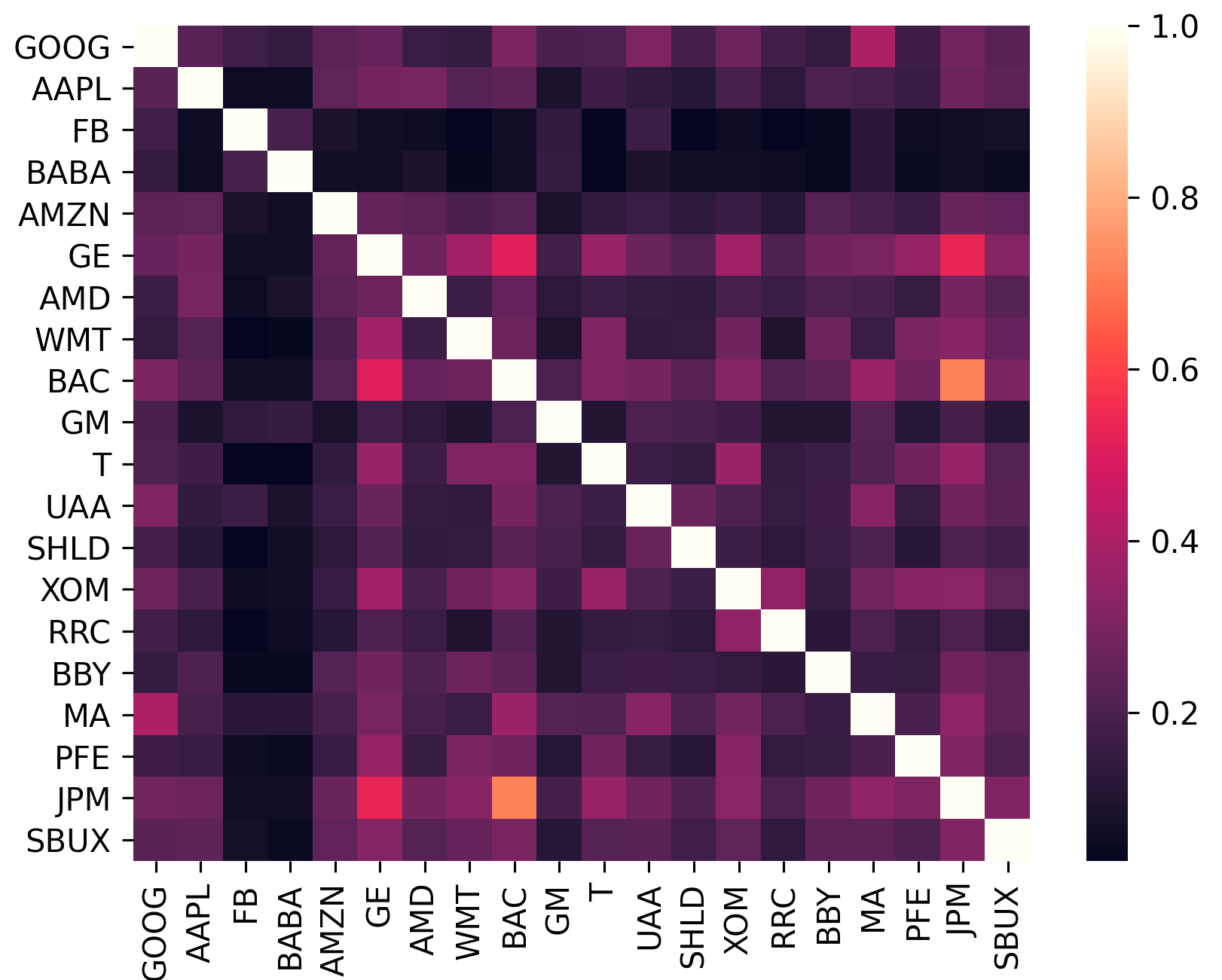
(Ce tracé a été généré à l'aide de plotting.plot_covariance )
ef = EfficientFrontier ( mu , S , weight_bounds = ( - 1 , 1 ))efficient_risk et efficient_return , PyPortfolioOpt offre la possibilité de former un portefeuille neutre par rapport au marché (c'est-à-dire que la somme des pondérations est égale à zéro). Cela n'est pas possible pour le portefeuille Max Sharpe et le portefeuille Min Volatilité car dans ces cas, ils ne sont pas invariants en termes d'effet de levier. La neutralité du marché nécessite des pondérations négatives : ef = EfficientFrontier ( mu , S , weight_bounds = ( - 1 , 1 ))
ef . efficient_return ( target_return = 0.2 , market_neutral = True ) ef = EfficientFrontier ( mu , S , weight_bounds = ( 0 , 0.1 )) L’un des problèmes de l’optimisation moyenne-variance est qu’elle conduit à de nombreux poids nuls. Bien que ceux-ci soient « optimaux » au sein de l’échantillon, de nombreuses recherches montrent que cette caractéristique conduit les portefeuilles à variance moyenne à sous-performer hors échantillon. À cette fin, j'ai introduit une fonction objectif qui peut réduire le nombre de poids négligeables pour chacune des fonctions objectives. Essentiellement, cela ajoute une pénalité (paramétrée par gamma ) sur les petits poids, avec un terme qui ressemble à la régularisation L2 en machine learning. Il peut être nécessaire d'essayer plusieurs valeurs gamma pour obtenir le nombre de poids non négligeable souhaité. Pour le portefeuille test de 20 titres, gamma ~ 1 suffit
ef = EfficientFrontier ( mu , S )
ef . add_objective ( objective_functions . L2_reg , gamma = 1 )
ef . max_sharpe ()Depuis la version 0.5.0, nous prenons désormais en charge l'allocation d'actifs Black-Litterman, qui vous permet de combiner une estimation préalable des rendements (par exemple les rendements implicites du marché) avec vos propres opinions pour former une estimation a posteriori. Cela donne lieu à de bien meilleures estimations des rendements attendus que la simple utilisation du rendement historique moyen. Consultez la documentation pour une discussion de la théorie, ainsi que des conseils sur le formatage des entrées.
S = risk_models . sample_cov ( df )
viewdict = { "AAPL" : 0.20 , "BBY" : - 0.30 , "BAC" : 0 , "SBUX" : - 0.2 , "T" : 0.131321 }
bl = BlackLittermanModel ( S , pi = "equal" , absolute_views = viewdict , omega = "default" )
rets = bl . bl_returns ()
ef = EfficientFrontier ( rets , S )
ef . max_sharpe () Les fonctionnalités ci-dessus concernent principalement la résolution de problèmes d'optimisation de la variance moyenne via la programmation quadratique (bien que cela soit pris en charge par cvxpy ). Cependant, nous proposons également différents optimiseurs :
Veuillez vous référer à la documentation pour en savoir plus.
Les tests sont écrits en pytest (beaucoup plus intuitif que unittest et les variantes à mon avis), et j'ai essayé d'assurer une couverture proche de 100 %. Exécutez les tests en accédant au répertoire du package et en exécutant simplement pytest sur la ligne de commande.
PyPortfolioOpt fournit un ensemble de données de test des rendements quotidiens pour 20 tickers :
[ 'GOOG' , 'AAPL' , 'FB' , 'BABA' , 'AMZN' , 'GE' , 'AMD' , 'WMT' , 'BAC' , 'GM' ,
'T' , 'UAA' , 'SHLD' , 'XOM' , 'RRC' , 'BBY' , 'MA' , 'PFE' , 'JPM' , 'SBUX' ]Ces tickers ont été sélectionnés de manière informelle pour répondre à plusieurs critères :
Actuellement, les tests n’ont pas exploré tous les cas extrêmes et toutes les combinaisons de fonctions et de paramètres objectifs. Cependant, chaque méthode et paramètre a été testé pour fonctionner comme prévu.
Si vous utilisez PyPortfolioOpt pour des travaux publiés, veuillez citer l'article JOSS.
Chaîne de citation :
Martin, R. A., (2021). PyPortfolioOpt: portfolio optimization in Python. Journal of Open Source Software, 6(61), 3066, https://doi.org/10.21105/joss.03066
BibTex ::
@article { Martin2021 ,
doi = { 10.21105/joss.03066 } ,
url = { https://doi.org/10.21105/joss.03066 } ,
year = { 2021 } ,
publisher = { The Open Journal } ,
volume = { 6 } ,
number = { 61 } ,
pages = { 3066 } ,
author = { Robert Andrew Martin } ,
title = { PyPortfolioOpt: portfolio optimization in Python } ,
journal = { Journal of Open Source Software }
}Les contributions sont les bienvenues . Jetez un œil au Guide de contribution pour en savoir plus.
Je tiens à remercier toutes les personnes qui ont contribué à PyPortfolioOpt depuis sa sortie en 2018. Un merci spécial à :