Inverser Matrix à l'aide d'un réseau neuronal.
Les matrices inversées présentent des défis uniques pour les réseaux de neurones, principalement en raison de limitations inhérentes à effectuer des opérations arithmétiques précises telles que la multiplication et la division des activations. Les réseaux denses traditionnels ont souvent besoin d'aide avec ces tâches, car elles ne sont pas explicitement conçues pour gérer les complexités impliquées dans l'inversion de la matrice. Les expériences menées avec des réseaux de neurones denses simples ont montré des difficultés importantes à réaliser des inversions de matrice précises. Malgré diverses tentatives pour optimiser l'architecture et le processus de formation, les résultats nécessitent souvent une amélioration. Cependant, la transition vers une architecture plus complexe - un réseau résiduel à 7 couches (RESNET) - peut entraîner des améliorations marquées des performances.
L'architecture Resnet, connue pour sa capacité à apprendre des représentations profondes à travers des connexions résiduelles, s'est avérée efficace pour lutter contre l'inversion de la matrice. Avec des millions de paramètres, ce réseau peut capturer des modèles complexes dans les données que les modèles plus simples ne peuvent pas. Cependant, cette complexité a un coût: des données de formation substantielles sont nécessaires pour une généralisation efficace.
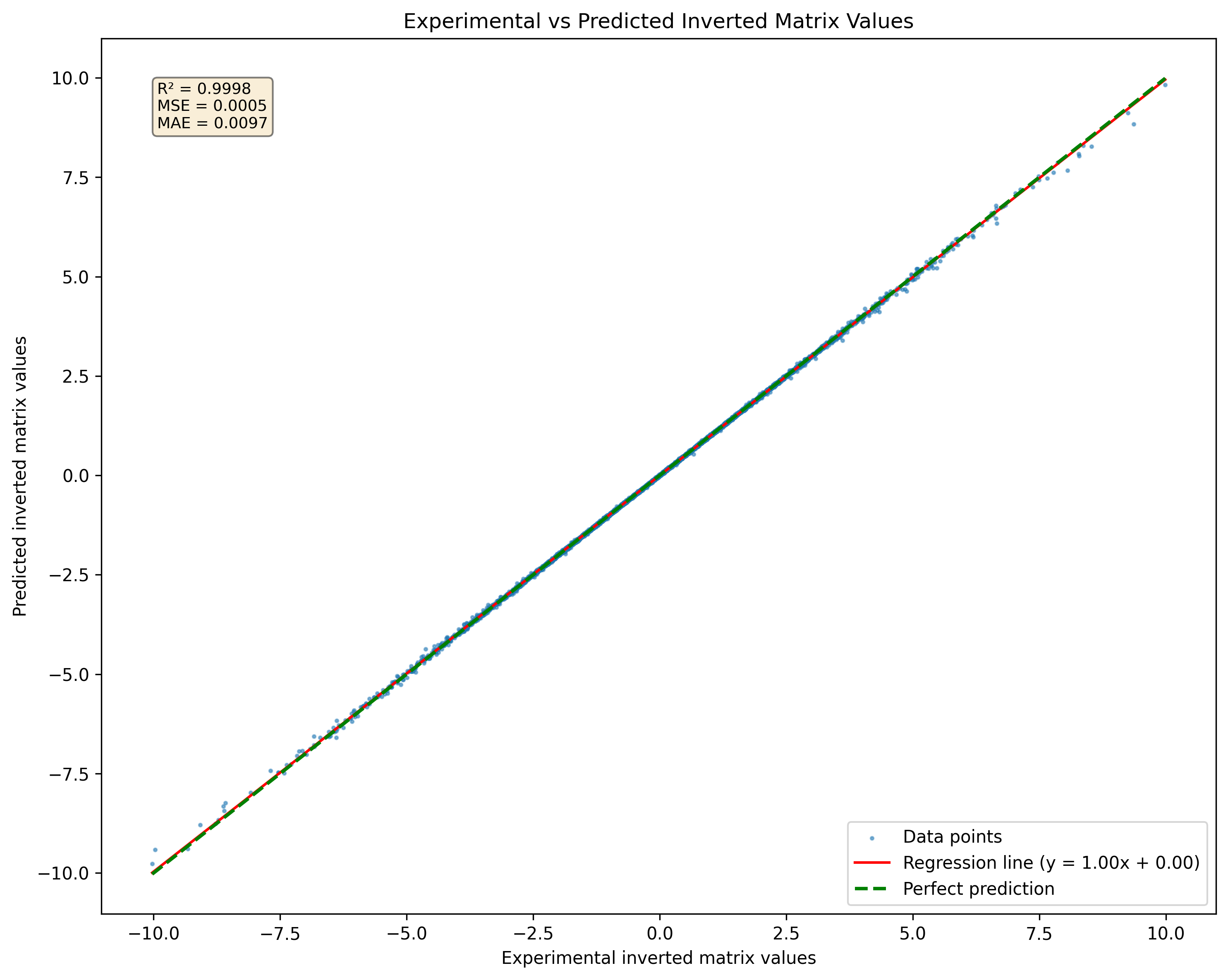Figure 1: La visualisation d'un réseau neuronal a prédit une matrice inversée pour un ensemble de matrices 3x3 jamais vues dans l'ensemble de données
Pour évaluer les performances du réseau neuronal pour prédire les inversions de la matrice, une fonction de perte spécifique est utilisée:
Dans cette équation:
L'objectif est de minimiser la différence entre la matrice d'identité et le produit de la matrice d'origine et son inverse prévu. Cette fonction de perte mesure efficacement à quel point l'inverse prédit est proche d'être précis.
De plus, si
Cette fonction de perte offre des avantages distincts par rapport aux fonctions de perte traditionnelles telles que l'erreur quadratique moyenne (MSE) ou l'erreur absolue moyenne (MAE).
Mesure directe de la précision de l'inversion L'objectif principal de l'inversion de la matrice est de garantir que le produit d'une matrice et son inverse donne la matrice d'identité. La fonction de perte capture directement cette exigence en mesurant l'écart par rapport à la matrice d'identité. En revanche, MSE et MAE se concentrent sur les différences entre les valeurs prédites et les valeurs réelles sans aborder explicitement la propriété fondamentale de l'inversion de la matrice.
L'accent mis sur l'intégrité structurelle en utilisant une fonction de perte qui évalue à quel point le produit AA - 1AA-1 est proche de II, il met l'accent sur le maintien de l'intégrité structurelle des matrices impliquées. Ceci est particulièrement important dans les applications où la préservation des relations linéaires est cruciale. Les fonctions de perte traditionnelles comme MSE et MAE ne tiennent pas compte de cet aspect structurel, conduisant potentiellement à des solutions qui minimisent l'erreur mais qui ne satisfont pas aux exigences mathématiques de l'inversion de la matrice.
Applicabilité aux matrices non singulières Cette fonction de perte suppose intrinsèquement que les matrices inversées sont non singulaires (c'est-à-dire inversibles). Dans les scénarios où des matrices singulières sont présentes, les fonctions de perte traditionnelles peuvent donner des résultats trompeurs car ils ne tiennent pas compte de l'impossibilité d'obtenir une inverse valide. La fonction de perte proposée met en évidence cette limitation en produisant des erreurs plus importantes lors de la tentative d'inversion des matrices singulières.
Une limitation significative lors de l'utilisation de réseaux de neurones pour l'inversion matricielle est leur incapacité à gérer efficacement les matrices singulières. Une matrice singulière n'a pas d'inverse; Ainsi, toute tentative d'un réseau neuronal de prédire un inverse pour de telles matrices donnera des résultats incorrects. En pratique, si une matrice singulière est présentée lors de la formation ou de l'inférence, le réseau peut toujours produire un résultat, mais cette sortie ne sera pas valide ou significative. Cette limitation souligne l'importance de garantir que les données de formation se compose de matrices non singulaires chaque fois que possible.
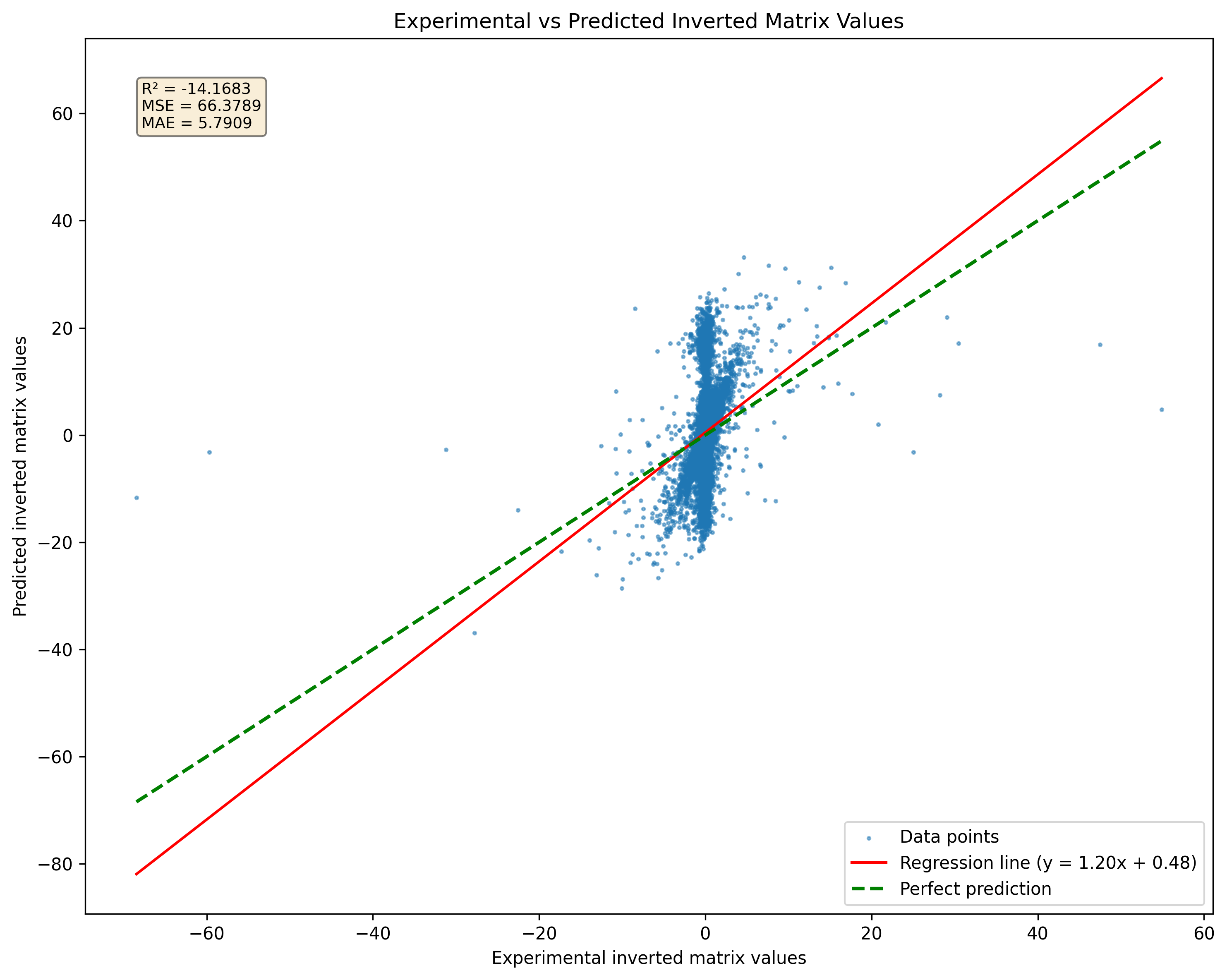Figure 2: Comparaison de la prédiction du modèle pour les matrices singulières par rapport aux pseudoinversions. Notez que le modèle produira des résultats quelle que soit la singularité matricielle.
La recherche indique qu'un modèle RESNET peut mémoriser une bonne quantité d'échantillons sans perte de précision significative. Cependant, l'augmentation de la taille de l'ensemble de données à 10 millions d'échantillons peut entraîner une sur-ajustement sévère. Ce sur-ajustement se produit malgré le grand volume de données, soulignant que la simple augmentation de la taille de l'ensemble de données ne garantit pas une meilleure généralisation pour les modèles complexes. Pour relever ce défi, une stratégie de génération de données continue peut être adoptée. Au lieu de s'appuyer sur un ensemble de données statique, des échantillons peuvent être générés à la volée et transmis au réseau lorsqu'ils sont créés. Cette approche, qui est cruciale pour atténuer le sur-ajustement, fournit non seulement une gamme diversifiée d'exemples de formation, mais garantit également que le modèle est exposé à un ensemble de données en constante évolution.
En résumé, alors que l'inversion de la matrice est intrinsèquement difficile pour les réseaux de neurones en raison de limitations des opérations arithmétiques, la mise à profit d'architectures avancées comme Resnet peut donner de meilleurs résultats. Cependant, une attention particulière doit être accordée aux exigences de données et aux risques sur l'ajustement. La génération continue d'échantillons de formation peut améliorer le processus d'apprentissage du modèle et améliorer les performances des tâches d'inversion de la matrice. Cette version maintient un ton impersonnel tout en discutant des défis et des stratégies dans la formation des réseaux de neurones pour l'inversion de la matrice.
DeepMatrixinversion est distribué sous licence LGPLV3
Pour en savoir plus, comment les licences fonctionnent, veuillez lire le dossier "Licence" ou accéder à "http://www.gnu.org/licenses/lgpl-3.0.html"
DeepMatrixinversion est actuellement la propriété de Giuseppe Marco Randazzo.
Pour installer le référentiel DeepMatrixinversion, vous pouvez choisir entre l'utilisation de la poésie, PIP ou PIPX ci-dessous les instructions pour les deux méthodes.
git clone https://github.com/gmrandazzo/DeepMatrixInversion.git
cd DeepMatrixInversion
python3 -m venv .venv
. .venv/bin/activate
pip install poetry
poetry install
Cela mettra en place votre environnement avec tous les packages nécessaires pour exécuter DeepMatrixinversion.
Créer un environnement virtuel et installer DeppMatrixinversion avec PIP
python3 -m venv .venv
. .venv/bin/activate
pip install git+https://github.com/gmrandazzo/DeepMatrixInversion.git
Si vous préférez utiliser PIPX, qui vous permet d'installer des applications Python dans des environnements isolés, suivez ces étapes:
python3 -m pip install --user pipx
apt-get install pipx
brew install pipx
sudo dnf install pipx
pipx install git + https: //github.com/gmrandazzo/deepmatrixinversion.git
Pour former un modèle qui peut effectuer une inversion matricielle, vous utiliserez la commande dmxtrain. Cette commande vous permet de spécifier divers paramètres qui contrôlent le processus de formation, tels que la taille des matrices, la plage de valeurs et la durée de formation.
dmxtrain --msize < matrix_size > --rmin < min_value > --rmax < max_value > --epochs < number_of_epochs > --batch_size < size_of_batches > --n_repeats < number_of_repeats > --mout < output_model_path > dmxtrain --msize --rmin -1 --rmax 1 --epochs 5000 --batch_size 1024 --n_repeats 3 --mout ./Model_3x3
--msize <matrix_size>: Specifies the size of the square matrices to be generated for training. For example, 3 for 3x3 matrices.
--rmin <min_value>: Sets the minimum value for the random elements in the matrices. For instance, -1 will allow negative values.
--rmax <max_value>: Sets the maximum value for the random elements in the matrices. For example, 1 will limit values to a maximum of 1.
--epochs <number_of_epochs>: Defines how many epochs (complete passes through the training dataset) to run during training. A higher number typically leads to better performance; in this case, 5000.
--batch_size <size_of_batches>: Determines how many samples are processed before the model is updated. A batch size of 1024 means that 1024 samples are used in each iteration.
--n_repeats <number_of_repeats>: Indicates how many times to repeat the training process with different random seeds or initializations. This can help ensure robustness; for instance, repeating 3 times.
--mout <output_model_path>: Specifies where to save the trained model. In this example, it saves to ./Model_3x3.
Une fois que vous avez formé votre modèle, vous pouvez l'utiliser pour effectuer une inversion de matrice sur de nouvelles matrices d'entrée. La commande pour l'inférence est DMXinvert, qui prend une matrice d'entrée et sortira son inverse.
AVERTISSEMENT: DMXinvert peut inverser une matrice plus grande que celle utilisée pour former le modèle à travers la formule d'inversion de la matrice Sherman-Morrison-Woodbury. Cette fonction ne fonctionne qu'avec des matrices dont la taille du bloc peut être divisée par la taille du bloc d'entraînement du modèle sans rappel. La fonctionnalité est très expérimentale et peut devoir être révisée.
dmxinvert --inputmx <input_matrix_file> --inverseout <output_csv_file> --model <model_path>
dmxinvert --inputmx input_matrix.csv --inverseout output_inverse.csv --model ./Model_3x3_*
--inputmx <input_matrix_file>: Specifies the path to the input matrix file that you want to invert. This file should contain a valid matrix format (e.g., CSV).
--inverseout <output_csv_file>: Indicates where to save the resulting inverted matrix. The output will be saved in CSV format.
--model <model_path>: Provides the path to the trained model that will be used for performing the inversion.
Générer un ensemble de données artificielles avec matrice d'entrée et sortie inversée se fait trought dmx dmxdatasetGenerator
dmxdatasetgenerator 3 10 -1 1 test_3x3_range_-1+1
Cela générera 10 matrices de taille 3x3 avec des nombres dans une plage de -1 à +1.
dmxdatasetgenerator [matrix size] [number of samples] [range min] [range max] [outname_prefix]
Ensuite, l'ensemble de données peut être validé à l'aide de dmxdatasetverify
dmxdatasetverify test_3x3_range_-1+1_matrices_3x3.mx test_3x3_range_-1+1_matrices_inverted_3x3.mx invertible
Dataset valid.
dmxdatasetverify [dataset matrix to invert] [dataset matrix inverted] [type: invertible or singular]
Le fichier de matrice d'entrée doit être formaté comme suit:
0.24077047370124594,-0.5012474139608847,-0.5409542929032876
-0.6257864520097793,-0.030705148203584942,-0.13723920334288975
-0.48095686716222064,0.19220406568380666,-0.34750000491973854
END
0.4575368007107925,0.9627977617090073,-0.4115240560547333
0.5191433428806012,0.9391491187187144,-0.000952683255491138
-0.17757763984424968,-0.7696584771443977,-0.9619759413623306
END
-0.49823271153034154,0.31993947803488587,0.9380291202366384
0.443652116558352,0.16745965310481048,-0.267270356721347
0.7075720067281346,-0.3310912886946993,-0.12013367141105102
END
Chaque bloc de nombres représente une matrice séparée suivie d'un marqueur final indiquant la fin de cette matrice.
