Rubik's Cube Solver pour de très grands cubes.
Résout n'importe quel cube de n'importe quelle taille de 1 à 65536. Le code peut être facilement modifié pour gérer des cubes encore plus grands. Cependant, la principale limitation est la quantité de mémoire sur un système et la durée nécessaire pour résoudre. Le temps de résolution augmente ~ n ^ 2, ce qui signifie qu'il faut 4 à 5 fois de plus pour résoudre un cube qui est 2x plus grand dans chaque dimension.
Un cube de 1024 couches peut être résolu en environ 1,5 seconde. Un cube en couches de 16384 peut être résolu en environ 20 minutes.
YouTube: Résoudre 65536 Couches YouTube: Résolution de couches 32768
Image de la face avant d'un cube 32768
Résout les centres puis les coins puis les bords
Les centres sont résolus en 15 étapes où chaque étape déplace toutes les pièces d'une certaine couleur d'un visage au visage souhaité. Par exemple: une scène déplace toutes les pièces vertes sur le visage blanc vers le visage vert. Répétez ceci pour toutes les couleurs et les visages.
Le solveur utilise le commutateur décrit ici qui peut déplacer des pièces centrales d'un quadrant d'un visage à un quartier sur une autre face. Une propriété très importante de ce commutateur est qui peut être modifiée pour déplacer de nombreuses pièces en une seule rangée en même temps. Pour les très grands cubes, cela signifie qu'il peut déplacer des centaines sinon des milliers de pièces en une seule opération. Le nombre moyen de mouvements k = (2 * p + 5) / p où p est le nombre de pièces qui peuvent être déplacées par opération. K s'approche rapidement 2 à mesure que la taille du cube augmente.
Les coins sont résolus en utilisant une méthode de base de force brute pour déplacer le coin en place, puis tournant jusqu'à ce que les faces soient orientées correctement. Will Smith peut expliquer: https://www.youtube.com/watch?v=wbzkdrc9vqs
Les bords sont résolus en déplaçant chaque paire de bords vers la face avant, puis en échangeant les pièces souhaitées du bord gauche au bord droit. Un certain nombre de fonctions si nécessaire pour résoudre ou prévenir les problèmes de parité.
Les rotations du visage sont essentiellement gratuites. Au lieu de déplacer toutes les pièces sur une face donnée (n ^ 2 pièces) pour effectuer une rotation, le solveur modifie simplement le système de coordonnées utilisé pour lire / écrire sur le visage. Cela permet d'économiser une énorme quantité d'échange de données.
// Virtually rotate this face by q * 90 degrees
inline void Face::RotatefaceCW ( const int q)
{
orientation = (orientation + q) & 3 ;
}
// Gets the value of this face at coordinates r = row, c = column
inline const byte Face::GetRC ( const uint r, const uint c) const
{
switch (orientation) {
case 0 :
return data[(r << BS) + c];
case 1 :
return data[(c << BS) + (R1 - r)];
case 2 :
return data[((R1 - r) << BS) + (R1 - c)];
case 3 :
return data[((R1 - c) << BS) + r];
default :
return 0 ;
}
}Ce code comprend un exportateur d'image simple qui est utilisé pour rendre chaque visage dans une image.
https://www.nayuki.io/page/tiny-png-utput
https://github.com/nayuki/nayuki-web-published-Code
Tiny PNG Sortie est une petite bibliothèque autonome, disponible en C et C ++, qui prend RGB8.8.8 pixels et écrit un fichier PNG.
Le nombre total de mouvements peut être estimé en utilisant une formule simple. En supposant que le cube est suffisamment randomisé, nous pouvons nous attendre à ce que le premier visage soit résolu et donc 5/6 des pièces devront être déplacées. La deuxième face sera résolue 1/5 et nécessitera que 4/5 des pièces soient déplacées. La troisième face 3/4, la quatrième face 2/3, la cinquième face 1/2 et la dernière face seront complètement résolues. Le nombre moyen de mouvements (k) pour déplacer une pièce unique peut être estimé expérimentalement à ~ 2,1. La valeur de K diminue à mesure que la taille du cube augmente. La valeur ne peut jamais être inférieure à 2 car le commutateur nécessite que chaque pièce soit déplacée au moins 2 fois.
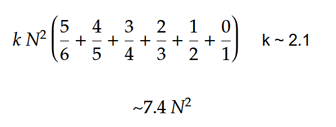
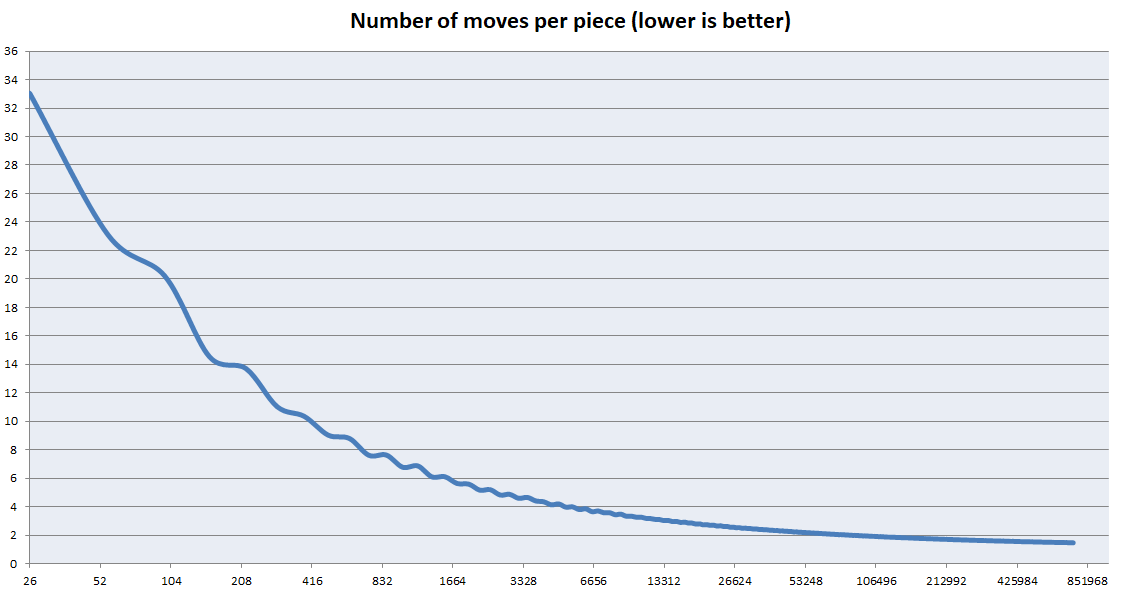
Cet algorithme est optimisé pour les très grands cubes. Cependant, c'est terrible pour les petits cubes. Les principales optimisations étaient axées sur la résolution des centres le plus rapidement possible et aucune considération n'a été accordée à la résolution des bords. Cependant, la taille des bords est insignifiante par rapport aux centres à mesure que la taille du cube augmente. Le graphique ci-dessous montre comment le nombre moyen de mouvements par pièce diminue avec des cubes plus grands. Remarque: Ce n'est pas un graphique de k. C'est un graphique de (total mouvements) / (nombre de pièces)
cmake -B build -S .
cd build
cmake --build .
RCube/RCube