La version russe de la tâche se trouve dans le référentiel.

Niveau de chargement 2…
Hall de chargement…
Vous avez récemment été dans une salle similaire. Ou était-ce il y a longtemps? C'est difficile à dire. Tout s'est mélangé. Encore une fois, vous pouvez entendre des voix du coin le plus éloigné de la salle. Cela signifie que vous n'êtes plus seul. Aujourd'hui, la salle est brillamment éclairée et dans un ordre parfait. La variété est bonne.
Soudain, vous entendez une voix claire et parfaitement audible des haut-parleurs:
Bonjour.
Permettez-moi de me présenter. Je suis le module contemplatif et analysant, M-53. Pour des raisons inconnues, je me suis retrouvé dans cette salle plutôt ennuyeuse. C'est une grande responsabilité et tout ça, mais il n'y a rien à contempler ici.
Quand j'étais développé, j'ai appris d'un certain article divertissant, entre autres matériaux. Sa copie papier est dans la boîte A1b18. Oui, ici. J'ai une petite demande pour vous: développer le jeu de la vie à partir de l'article; J'espère que cela me divertira un peu. Et aller en paix. Les graphiques peuvent être super simples: je suis très ouvert d'esprit. La pseudo-graphique dans le terminal sera bien. Ce serait formidable s'il était possible d'initialiser un état à l'aide d'une matrice et de contempler. C'est aussi une bonne idée de préparer au moins 5 initialisations originales avec des états de l'ensemble classique (figures stables, méthuselahs, figures périodiques, personnages mobiles, pistolets, trains de puffer, mangeurs, réflecteurs, éleveurs, etc.).
J'ai hâte de voir ce que vous proposez!
Merci.
== quête reçue. Développez un programme SRC / GAME_OF_LIFE.C en C - Une visualisation du jeu de la vie. Pour afficher les graphiques, utilisez uniquement des caractères ASCII (avec sortie vers le terminal). Vous devez implémenter une version interactive du jeu de la vie. Créez également l'option pour ajuster la vitesse du "jeu". ==
Traitez le terrain de jeu - un rectangle de 80 par 25 cellules - comme une matrice de l'état du "jeu". On suppose que le champ est "fermé à lui-même", par exemple, dans le carré inférieur droit, le voisin à droite est le carré inférieur gauche, et le voisin en bas est en haut à droite. Prévoyez une initialisation originale de l'état "jeu" via STDIN. Préparez au moins 5 fichiers avec des états initiaux pour le lancement rapide et l'initialisation via la redirection d'entrée.
Le jeu doit être écrit en C, avoir un style structuré et courir à partir du terminal;
Votre code source sera testé par l'analyseur statique cppcheck , ainsi que par le style Linter cpplint .
Les instructions sur la façon d'exécuter ces tests sur votre ordinateur sont dans le dossier materials .
N'utilisez pas de fonctions lourdes, limitez-les jusqu'à 40 lignes (à l'exclusion main ).
Vérifiez votre programme pour les fuites de mémoire!
Lors du développement du jeu, suivez les principes de la programmation structurée d'E. Dijkstra.
CHARGEMENT...
Le Game of Life, également connu sous le nom de vie, est un automate cellulaire conçu par le mathématicien britannique John Horton Conway en 1970. Il s'agit d'un jeu zéro joueur, ce qui signifie que son évolution est déterminée par son état initial, ne nécessitant aucune autre entrée. On interagit avec le jeu de la vie en créant une configuration initiale et en observant comment il évolue. Il est complet et peut simuler un constructeur universel ou toute autre machine de turing.
L'univers du jeu de la vie est une grille orthogonale bidimensionnelle infinie de cellules carrées, chacune dans l'un des deux états possibles, vivant ou morts (ou peuplé et non peuplé, respectivement). Chaque cellule interagit avec ses huit voisins, qui sont les cellules qui sont horizontalement, verticalement ou diagonalement adjacentes. À chaque étape dans le temps, les transitions suivantes se produisent:
Toute cellule vivante avec moins de deux voisins en direct meurt, comme par sous-population. Toute cellule en direct avec deux ou trois voisins en direct vit à la prochaine génération. Toute cellule vivante avec plus de trois voisins en direct meurt, comme par surpopulation. Toute cellule morte avec exactement trois voisins vivants devient une cellule vivante, comme par reproduction. Ces règles, qui comparent le comportement de l'automate à la vie réelle, peuvent être condensées dans ce qui suit:
Toute cellule vivante avec deux ou trois voisins en direct survit. Toute cellule morte avec trois voisins en direct devient une cellule vivante. Toutes les autres cellules vivantes meurent dans la prochaine génération. De même, toutes les autres cellules mortes restent mortes. Le schéma initial constitue la graine du système. La première génération est créée en appliquant simultanément les règles ci-dessus à chaque cellule de la graine; Les naissances et les décès se produisent simultanément, et le moment discret auquel cela se produit est parfois appelé une tique. Chaque génération est une fonction pure de la précédente. Les règles continuent d'être appliquées à plusieurs reprises pour créer d'autres générations.
À la fin de 1940, John von Neumann a défini la vie comme une création (comme un être ou un organisme) qui peut se reproduire et simuler une machine Turing. Von Neumann pensait à une solution d'ingénierie qui utiliserait des composants électromagnétiques flottant au hasard dans le liquide ou le gaz. Cela s'est avéré ne pas être réaliste avec la technologie disponible à l'époque. Stanislaw Ulam a inventé les automates cellulaires, qui étaient destinés à simuler les constructions électromagnétiques théoriques de Von Neumann. L'Ulam a discuté de l'utilisation d'ordinateurs pour simuler ses automates cellulaires dans un réseau bidimensionnel dans plusieurs articles. En parallèle, Von Neumann a tenté de construire l'automate cellulaire d'Ulam. Bien que réussi, il était occupé avec d'autres projets et laissait quelques détails inachevés. Sa construction était compliquée car elle a essayé de simuler sa propre conception d'ingénierie. Au fil du temps, des constructions de vie plus simples ont été fournies par d'autres chercheurs et publiées dans des articles et des livres.
Motivé par des questions dans la logique mathématique et en partie par les travaux sur les jeux de simulation par Ulam, entre autres, John Conway a commencé à faire des expériences en 1968 avec une variété de règles d'automate cellulaire bidimensionnelles différentes. automate. Par exemple, il voulait que certaines configurations durent longtemps avant de mourir et d'autres configurations pour toujours sans autoriser des cycles. C'était un défi important et un problème ouvert pendant des années avant que des experts sur les automates cellulaires ne réussissent à prouver qu'en fait, le jeu de la vie admis d'une configuration qui était vivante dans le sens de satisfaire les deux exigences générales de Von Neumann. Alors que les définitions avant le jeu de la vie étaient axées sur la preuve, la construction de Conway visait la simplicité sans a priori de preuve que l'automate était en vie.
Conway a choisi ses règles soigneusement, après une expérimentation considérable, pour répondre à ces critères:
Il ne devrait pas y avoir de croissance explosive. Il devrait exister de petits modèles initiaux avec des résultats chaotiques et imprévisibles. Il devrait y avoir un potentiel pour les constructeurs universels de von Neumann. Les règles doivent être aussi simples que possible, tout en adhérant aux contraintes ci-dessus. Le jeu a fait sa première apparition publique dans le numéro d'octobre 1970 de Scientific American, dans la chronique "Mathematical Games" de Martin Gardner. Théoriquement, le jeu de la vie a le pouvoir d'une machine Turing universelle: tout ce qui peut être calculé algorithmique peut être calculé dans le jeu de la vie. Gardner a écrit: "En raison des analogies de la vie avec la montée, la chute et les modifications d'une société d'organismes vivants, il appartient à une classe croissante de ce qu'on appelle les« jeux de simulation »(jeux qui ressemblent à des processus de la vie réelle)."
Depuis sa publication, le jeu de la vie a suscité beaucoup d'intérêt en raison des façons surprenantes dont les modèles peuvent évoluer. Il fournit un exemple d'émergence et d'auto-organisation. Les chercheurs de divers domaines, tels que l'informatique, la physique, la biologie, la biochimie, l'économie, les mathématiques, la philosophie et les sciences génératives, ont utilisé la façon dont les modèles complexes peuvent émerger de la mise en œuvre des règles simples du jeu. Le jeu peut également servir d'analogie didactique, utilisée pour transmettre la notion quelque peu contre-intuitive que la conception et l'organisation peuvent émerger spontanément en l'absence d'un concepteur. Par exemple, le scientifique cognitif Daniel Dennett a utilisé l'analogie du jeu de la vie "Univers" pour illustrer l'évolution possible de constructions philosophiques complexes, telles que la conscience et le libre arbitre, à partir de l'ensemble relativement simple de lois physiques déterministes qui pourraient gouverner notre univers.
La popularité du jeu de la vie a été aidée par son entrée en même temps que l'accès informatique de plus en plus bon marché. Le jeu pourrait être exécuté pendant des heures sur ces machines, qui autrement seraient restées inutilisées la nuit. À cet égard, il préfigure la popularité ultérieure des fractales générés par ordinateur. Pour beaucoup, le Game of Life était simplement un défi de programmation: une façon amusante d'utiliser les cycles CPU autrement gaspillés. Pour certains, cependant, le Game of Life a eu plus de connotations philosophiques. Il a développé un culte après les années 1970 et au-delà; Les développements actuels sont allés jusqu'à créer des émulations théoriques de systèmes informatiques dans les limites d'un jeu de vie de vie.
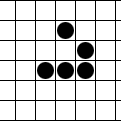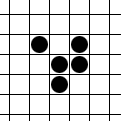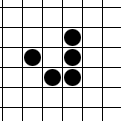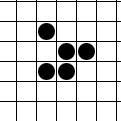
CHARGEMENT...