
et les tâches Fibre dans React, et différentes tâches Fibre ont des priorités différentes pour traiter en premier les tâches avec une priorité élevée. Par exemple, les clics et les saisies de l'utilisateur sont des tâches hautement prioritaires, car les opérations de l'utilisateur espèrent certainement avoir des effets immédiats, afin d'améliorer l'expérience utilisateur. Par exemple, la priorité des événements d'animation doit être inférieure. Une fois qu’une nouvelle tâche hautement prioritaire entre dans la file d’attente, React doit d’abord la traiter.
Pour stocker ces tâches, il existe deux pools de tâches dans React.
// Les tâches sont stockées sur un tas min var taskQueue = []; var timerQueue = [];
taskQueue et timerQueue sont tous deux des tableaux. Le premier stocke les tâches à exécuter immédiatement, tandis que le second stocke les tâches qui peuvent être retardées.
var nouvelleTâche = {
id : taskIdCounter++, // Marquer l'identifiant de la tâche
callback, // fonction de rappel prioritéLevel, // priorité de la tâche startTime, // heure de début de la tâche, point temporel expirationTime, // heure d'expiration, point temporel sortIndex : -1, // tri des tâches, la valeur provient de l'heure d'expiration, donc la valeur Plus la valeur est petite, plus la priorité est élevée}; Une fois qu'une nouvelle tâche arrive dans React, elle utilisera d'abord currentTime pour enregistrer l'heure actuelle (performance.now() ou Date.now()). paramètre delay, alors la tâche démarre le temps d'exécution startTime = currentTime + delay ;. Ensuite, si startTime > currentTime est établi, cela prouve que la tâche peut être reportée, alors la tâche entre dans timerQueue, sinon elle entre dans taskQueue.
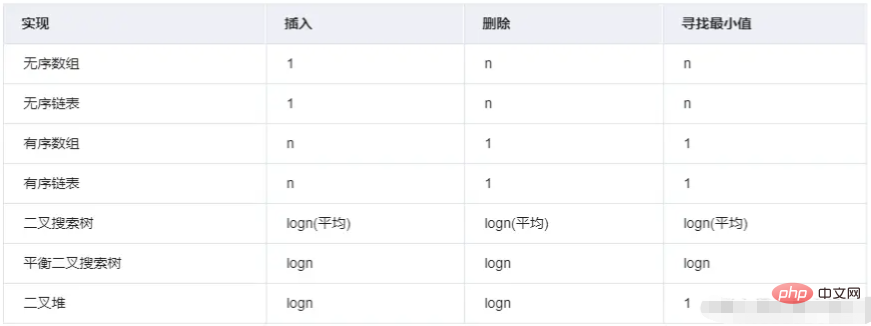
Comment React trouve-t-il la tâche avec la priorité la plus élevée ? Prenons taskQueue comme exemple. Il s'agit d'un pool de tâches dynamique (file d'attente des tâches) et le formulaire de données est un tableau. Bien sûr, vous pouvez trier par priorité, c'est-à-dire Array.sort Lorsqu'une nouvelle tâche est ajoutée à la file d'attente, elle est triée en premier, puis la tâche ayant la priorité la plus élevée est trouvée et exécutée. Mais la complexité temporelle moyenne d'Array.sort est O(nlogn), ce qui n'est pas la meilleure solution.
SortIndex est utilisé pour trier dans newTask de taskQueue. Cette valeur est tirée du délai d'expiration, ce qui signifie que plus la tâche prioritaire est élevée, plus elle doit être comprise et exécutée, donc le délai d'expiration sera plus petit. plus la priorité est élevée, plus le délai d'expiration est court, plus le sortIndex sera naturellement petit. En fait, c'est une file d'attente prioritaire .
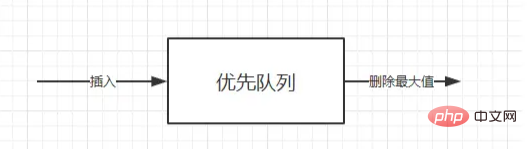
La file d'attente prioritaire est également une sorte de file d'attente ( tout d'abord, c'est une file d'attente, et deuxièmement, tail in, first out ). La seule différence est que l'ordre de retrait de la file d'attente prioritaire est basé sur la priorité dans certains cas ; , vous devrez peut-être rechercher L'élément minimum ou maximum dans l'ensemble d'éléments peut être exploité en utilisant la file d'attente prioritaire ADT La file d'attente prioritaire ADT est une structure de données qui prend en charge les opérations d'insertion et de suppression de valeur minimale (renvoi et suppression de l'élément minimum) ou. suppression de l'opération de valeur maximale (retour et suppression de l'élément minimum).
Si l'élément avec la plus petite valeur de clé a la priorité la plus élevée, alors cette file d'attente prioritaire est appelée file d'attente à priorité ascendante (c'est-à-dire que le plus petit élément est toujours supprimé en premier). De même, si l'élément avec la plus grande valeur de clé a la priorité la plus élevée, alors ce type de file d'attente prioritaire est appelé file d'attente à priorité décroissante (c'est-à-dire que l'élément le plus grand est toujours supprimé en premier puisque ces deux types sont symétriques, vous n'en avez besoin que) ; pour se concentrer sur l'un d'entre eux, comme la file d'attente prioritaire ascendante.
Par exemple : lorsque nous achetions des billets, nous faisions tous la queue et avions la même priorité. Celui qui était devant la file d'attente achetait le billet en premier. Mais ensuite un soldat est arrivé et il avait une priorité plus élevée et était directement dans la file d'attente. .Le devant.
Le tas minimum (petit tas racine, petit tas supérieur...) est utilisé dans React pour réaliser cette fonction. Cela consiste à transformer la taskQueue en un tas minimum, puis à supprimer la tâche principale pour l'exécution, à empiler la taskQueue et à la conserver en tant que structure de données de tas minimum. Lors de l'insertion d'une nouvelle tâche dans taskQueue, elle doit également être tassée et toujours conservée comme tas minimum.
: À certains endroits, le tas est appelé file d'attente prioritaire (ce n'est pas précis). Tout d'abord, il s'agit d'une file d'attente et a les caractéristiques d'une file d'attente, c'est-à-dire « premier entré, premier sorti ». . Deuxièmement, les éléments de cette file d'attente ont des priorités, et ceux ayant des priorités plus élevées seront classés en premier.
Pour être précis, un tas est un moyen d'implémenter une file d'attente prioritaire. Bien entendu, les files d’attente prioritaires peuvent également être mises en œuvre d’autres manières.
Nous avons déjà dit que le tri par tas est un tri instable, mais taskQueue espère que ce processus est stable, c'est-à-dire que s'il est possible que le délai d'expiration de deux tâches soit le même, alors cela dépend de qui entre. d'abord. Le pool de tâches est la valeur de l'identifiant de newTask. Chaque fois qu'une nouvelle tâche arrive, l'identifiant sera augmenté de 1.
fonction comparer (a, b) {
// Comparez d'abord l'index de tri, puis l'identifiant de la tâche.
const diff = a.sortIndex - b.sortIndex;
return diff !== 0 ? diff : a.id - b.id;
} Avant de comprendre le tas minimum, passons en revue les connaissances de base.
fait référence à un arbre ordonné dans lequel le degré des nœuds de l'arbre n'est pas supérieur à 2. C'est l'arbre le plus simple et le plus important.
est un arbre binaire dans lequel tous les nœuds de chaque niveau ont deux nœuds enfants, à l'exception du dernier niveau qui n'a aucun nœud enfant.
D'un point de vue graphique, un arbre binaire complet ressemble à un triangle.
Si le nombre de niveaux d'un arbre binaire est K et le nombre total de nœuds est (2^k) -1, alors c'est un arbre binaire complet.
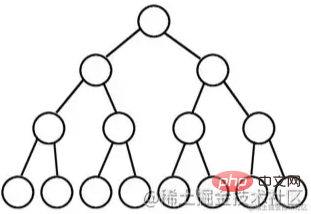
Un arbre binaire complet signifie « les filles ont les deux côtés » et est très parfait, c'est pourquoi on l'appelle un arbre binaire complet.
à l'exclusion des nœuds feuilles, le degré de tous les nœuds est 2. En d’autres termes, le degré de tous les nœuds ne peut être que 0 ou 2.
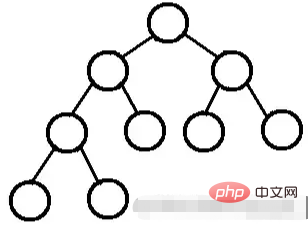
Un arbre binaire parfait n’a soit aucun enfant, soit les deux enfants.
Le texte anglais original de l'arbre binaire complet :
Un arbre binaire complet (FBT) est un arbre dans lequel chaque nœud autre que les feuilles a deux enfants.
Le texte anglais original de l'arbre binaire parfait :
Un arbre binaire parfait (PBT) est un arbre avec tous les nœuds feuilles à la même profondeur. Tous les nœuds internes ont le degré 2.
Tous les livres étrangers font référence aux premiers manuels traduits sur les arbres binaires complets et les arbres binaires parfaits, mais les premiers articles traduits sont mal traduits. Or, en Chine, on ne peut faire des erreurs que lorsqu’ils ont tort (tout le monde a tort, alors celui qui a tort a aussi raison. Par exemple, les lobbyistes…). Si vous souhaitez discuter de ces deux concepts avec des amis étrangers, vous devez y prêter attention.
Un arbre binaire(CBT) est un arbre binaire dans lequel chaque niveau, sauf éventuellement le dernier, est complètement rempli et tous les nœuds sont aussi à gauche que possible.
Un arbre binaire avec n nœuds de profondeur k, numérote les nœuds dans le. arbre de haut en bas et de gauche à droite. Si le nœud numéroté i (1≤i≤n) est dans l'arbre binaire avec le nœud numéroté i dans l'arbre binaire complet, si les positions sont les mêmes, l'arbre binaire est appelé un arbre binaire complet.
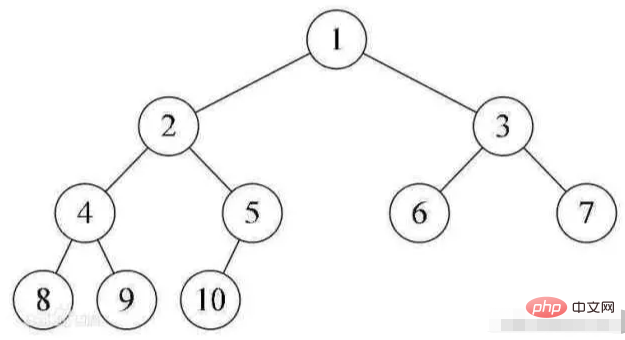
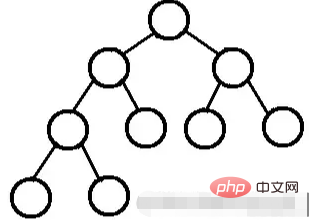
Le tas satisfait toujours les propriétés suivantes :
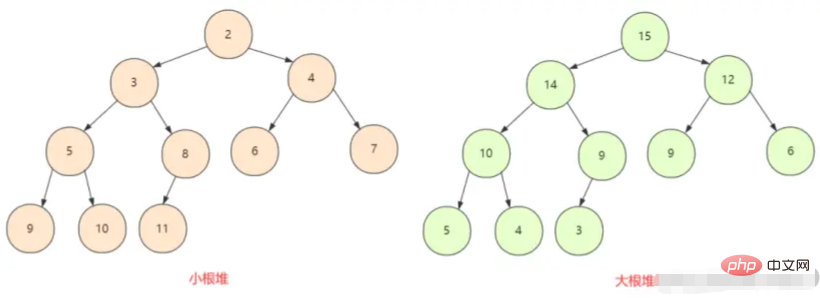
le tas esttoujours
le petit tas racine. Dans un arbre binaire complet, tous les nœuds sont plus grands (ou plus petits) que leurs nœuds enfants, il y a donc deux situations ici, le tas maximum et le tas minimum.
Le tas est généralement un tableau d'objets qui peut être considéré comme un arbre binaire complet . Bien entendu, les arbres binaires peuvent également être représentés par des tableaux.
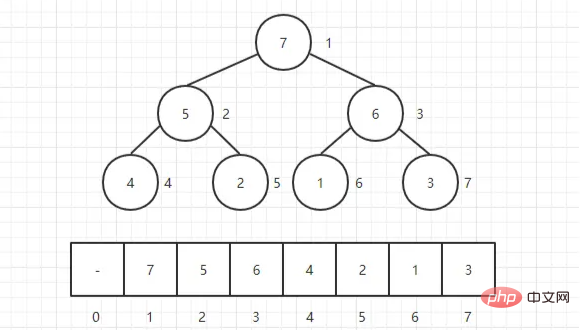
est de construire d'abord le tas, puis de l'ajuster.
, pour un arbre binaire (représentation matricielle), nous ajustons de bas en haut, en commençant par le "premier nœud non-feuille" et en ajustant vers l'avant. Les règles d'ajustement sont les suivantes :
La construction d'un tas est O(n). ) processus de complexité temporelle.
① Commencez par le premier nœud non-feuille pour juger le swap (shiftDown), afin que le nœud actuel et l'enfant puissent conserver les propriétés du tas
. ② Cependant, le remplacement ordinaire du nœud peut ne pas être un problème si l'échange casse les propriétés de la structure du tas. de l'enfant, il doit alors être re- ShiftDown le nœud échangé jusqu'à ce qu'il soit arrêté.
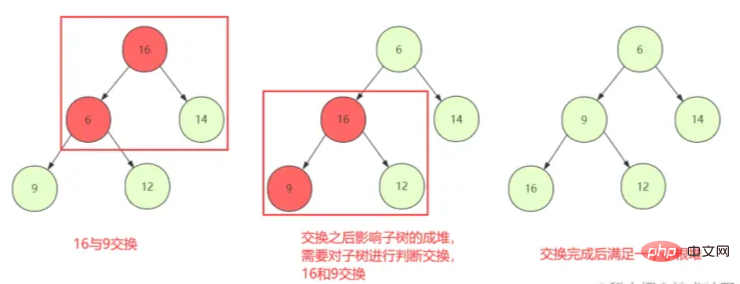
la structure du tas
détruire la structure du tas.
① Alors mettez simplement le dernier élément en premier. De cette façon, il vous suffit de juger le décalage d'échange (shiftDown), mais vous devez noter que la taille du tas entier a changé à ce moment-là. Nous n'utiliserons logiquement pas la position supprimée, nous devons donc inclure un tas. paramètre size lors de la conception de la fonction.
② Répétez l'opération ci-dessus jusqu'à ce que tous les éléments du tas soient obtenus.
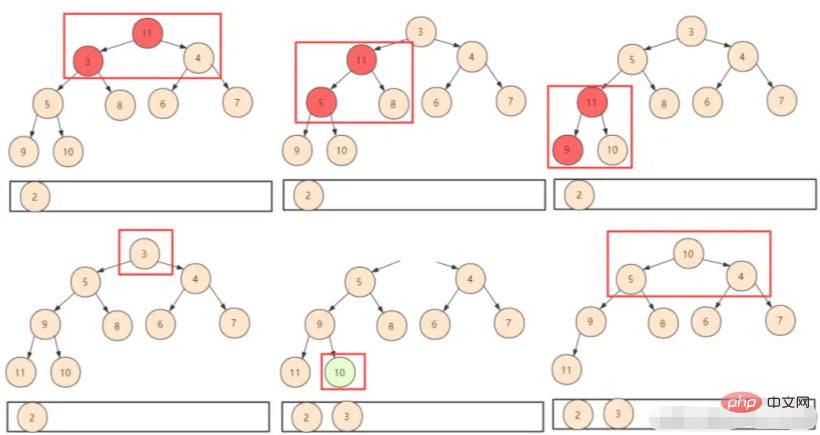
En termes d'analyse de la complexité de l'algorithme du tas, la complexité temporelle de construction du tas précédente était O(n). Chaque fois que le haut du tas est supprimé puis permuté vers le bas, le numéro de chacun est enregistré. De cette façon, la complexité est O(nlogn) et la complexité temporelle totale est O(n)+O(nlogn)=O(nlogn).
Heap conviennent pour maintenir la valeur maximale de la collection.
Une fois qu'un élément est sorti du tas, le coût de réajustement pour obtenir l'élément supérieur du tas (c'est-à-dire la deuxième valeur la plus élevée) est relativement faible, car une fois l'élément sorti, le tas est un semi-élément. -produit fini, et la deuxième valeur la plus élevée est obtenue à partir d'un produit semi-fini. Bien sûr, le coût est relativement faible et la complexité temporelle est O(logn), mais si elle est parcourue une fois pour trouver la deuxième valeur la plus élevée, la complexité temporelle est O(n).
code d'implémentation du code est écrit en Javascript ES6.
classeTas {
constructeur (données, composition) {
this.data = données ? données : [];
// Règles de comparaison : plus flexible, vous pouvez comparer des valeurs ou des objets this.compartor = comp comp ?
// Ajustement au tas (file d'attente prioritaire)
this.heapify();
}
tasifier() {
if(this.size() <= 1) return;
// Commencez l'ajustement à partir du premier nœud non-feuille, ou vous pouvez ajuster à partir du dernier élément for(let i=Math.floor((this.size()-2)/2); i>=0; i-- ) {
//Ajuster le tas. L'ajustement vers le bas peut également être implémenté en utilisant la récursion. Ici, l'itération est utilisée pour implémenter this.shiftDown(i);
}
}
// Ajustement vers le bas shiftDown(i) {
soit gauche = 2*i +1 ;
soit à droite = 2*i +2 ;
let len = this.size();
tandis que(i < len) {
laissez findIndex = i;
//L'enfant de gauche est "plus grand"
if(left < len && this.compartor(this.data[left], this.data[findIndex]) < 0) {
findIndex = gauche ;
}
// Le bon enfant est "plus grand"
if(right < len && this.compartor(this.data[right], this.data[findIndex]) < 0) {
findIndex = droite ;
}
si(je !== findIndex) {
//Échangez le nœud actuel avec une valeur plus grande [this.data[i], this.data[findIndex]] = [this.data[findIndex], this.data[i]];
// Après avoir ajusté cette couche, cela peut affecter les caractéristiques du tas de la couche inférieure, continuez donc à ajuster la couche inférieure (implémentation itérative ou récursive)
je = findIndex;
gauche = 2*i +1 ;
à droite = 2*i +2 ;
}
autre {
// Si aucun ajustement n'est nécessaire, sautez (doit sauter, sinon la boucle ne peut pas se terminer)
casser;
}
}
}
// Ajuster vers le haut shiftUp(i){
// Recherche l'indice du parent let parentIndex = Math.floor((i-1)/2);
// Ajuste le maximum à 0
while(parentIndex >=0 ) {
soit findIndex = i;
if(this.compartor(this.data[parentIndex], this.data[findIndex]) > 0) {
findIndex = parentIndex;
}
si(findIndex !== i) {
[this.data[i], this.data[findIndex]] = [this.data[findIndex], this.data[i]];
je = findIndex;
parentIndex = Math.floor((i-1)/2);
}
autre {
casser;
}
}
}
// Récupère le nombre de tous les éléments dans la taille du tas(){
renvoie this.data.length;
}
// Récupère le premier élément du tas peek(){
if(!this.size()) renvoie null ;
renvoie this.data[0] ;
}
//Ajouter un élément au tas push(x){
this.data.push(x);
this.shiftUp(this.data.length-1);
}
// Pop le premier élément du tas pop(){
if(!this.size()) renvoie null ;
laissez res = this.data[0];
si(this.size() == 1) {
this.data.pop();
}
autre {
this.data[0] = this.data[this.data.length-1];
this.data.length = this.data.length-1;
this.shiftDown(0);
}
retourner la résolution ;
}
} let arr = [2,9,8,6,3,10,5,7,4,1];
soit comp = (a, b) => ab;
let tas = new Heap(arr, comp);
soit res = [];
while(heap.size()) {
res.push(heap.pop());
}
console.log(res); L'élément dans arr peut également être un objet.
Le répertoire packages/scheduler dans le code source de React est le code lié au module de planification des tâches de React.
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src/Scheduler.js
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src /SchedulerMinHeap.js
/**
* Copyright (c) Facebook, Inc. et ses sociétés affiliées.
*
* Ce code source est sous licence MIT trouvée dans le
* Fichier LICENSE dans le répertoire racine de cette arborescence source.
*
* @flow strict
*/
tapez Heap = Array<Node> ;
tapez Noeud = {|
Identifiant : numéro,
sortIndex : nombre,
|};
fonction d'exportation push (tas : tas, nœud : nœud) : void {
const index = tas.longueur;
tas.push(nœud);
siftUp (tas, nœud, index);
}
fonction d'exportation coup d'oeil (tas : Heap) : Noeud |
const premier = tas[0];
return first === non défini ? null : first;
}
fonction d'exportation pop (tas : tas) : nœud null {
const premier = tas[0];
if (premier !== non défini) {
const dernier = tas.pop();
if (dernier !== premier) {
tas[0] = dernier ;
tamiser(tas, dernier, 0);
}
revenez d'abord;
} autre {
renvoie null ;
}
}
function siftUp (tas, nœud, i) {
soit index = i ;
tandis que (vrai) {
const parentIndex = (index - 1) >>> 1;
const parent = tas[parentIndex];
if (parent !== non défini && compare(parent, nœud) > 0) {
// Le parent est plus grand. Échangez les positions.
tas[parentIndex] = nœud ;
tas[index] = parent ;
index = parentIndex ;
} autre {
// Le parent est plus petit.
retour;
}
}
}
fonction siftDown (tas, nœud, i) {
soit index = i ;
const longueur = tas.longueur ;
while (index < longueur) {
const leftIndex = (index + 1) * 2 - 1;
const left = tas[leftIndex];
const rightIndex = leftIndex + 1 ;
const right = tas[rightIndex];
// Si le nœud gauche ou droit est plus petit, échangez avec le plus petit d'entre eux.
if (left !== non défini && compare(left, node) < 0) {
if (right !== non défini && compare(right, left) < 0) {
tas[index] = droite ;
tas[rightIndex] = nœud ;
index = rightIndex;
} autre {
tas[index] = gauche ;
tas[leftIndex] = nœud ;
index = indexgauche ;
}
} else if (right !== non défini && compare(right, node) < 0) {
tas[index] = droite ;
tas[rightIndex] = nœud ;
index = rightIndex;
} autre {
// Aucun des deux enfants n'est plus petit.
retour;
}
}
}
fonction comparer(a, b) {
// Comparez d'abord l'index de tri, puis l'identifiant de la tâche.
const diff = a.sortIndex - b.sortIndex;
return diff !== 0 ? diff : a.id - b.id;
} Le tas minimum que nous avons implémenté est légèrement différent de l'implémentation dans React, mais l'idée est la même, seul le code est écrit différemment.
la planification des tâches dans React est implémentée en utilisant le tas minimum. Si nous avons une certaine compréhension du tas minimum auparavant, nous apprendrons ce contenu plus rapidement. Personnellement, je pense à quel point il est important d’accumuler des connaissances dès le début, mais ce processus peut être ennuyeux. À l’heure actuelle, pensez-vous connaître certains algorithmes ? En fait, ces algorithmes sont d’entrée de gamme, et vous n’avez même pas encore commencé. Parce que dans le scénario de planification des tâches de React, les exigences à mettre en œuvre sont très claires, et les structures de données et les algorithmes à utiliser sont également clairs. Dans certains scénarios réels, nous connaissons les exigences spécifiques, mais nous ne savons pas quels résultats de données et quels algorithmes utiliser. Nous devons faire abstraction des exigences et concevoir des structures de données et des algorithmes spécifiques basés sur le modèle de données abstrait. .