MLE dengan Distribusi Normal - Lab

Perkenalan

Di lab ini, kita akan mempraktikkan rumus matematika yang kita lihat di pelajaran sebelumnya untuk melihat cara kerja MLE dengan distribusi normal.

Tujuan

Anda akan dapat:

Memahami dan menjelaskan cara kerja MLE dengan distribusi normal
Sesuaikan distribusi normal dengan data tertentu yang mengidentifikasi mean dan varians
Bandingkan secara visual distribusi pas vs. distribusi nyata

Catatan: *Derivasi detail seluruh persamaan MLE beserta pembuktiannya dapat dilihat di website ini. *

MLE dengan Python

Mari kita lihat contoh MLE dan perlengkapan distribusi dengan Python di bawah ini. Di sini scipy.stats.norm.fit menghitung parameter distribusi menggunakan Estimasi Kemungkinan Maksimum.

Impor perpustakaan yang diperlukan

 from scipy . stats import norm # for generating sample data and fitting distributions
import matplotlib . pyplot as plt
plt . style . use ( 'seaborn' )
import numpy as np

Hasilkan array 200 sampel acak dari dist normal dengan mean 0 dan stdv 1

 sample = None

Pemasangan distribusi melalui MLE

- Gunakan `stats.norm.fit(data)` untuk menyesuaikan distribusi dengan data di atas.

- Ini mengembalikan daftar dua parameter: (mean,: parameter[0] dan std: parameter[1]) melalui pendekatan MLE

 param = None

#param[0], param[1]
# (0.08241224761452863, 1.002987490235812)

Hitung PDF dari a) parameter data aktual b) parameter yang dipasang dengan `x = np.linspace(-5,5,100)`

 x = np . linspace ( - 5 , 5 , 100 )

# Generate the pdf from fitted parameters (fitted distribution)
fitted_pdf = None
# Generate the pdf without fitting (normal distribution non fitted)
normal_pdf = None

Visualisasikan kedua PDF

 # Your code here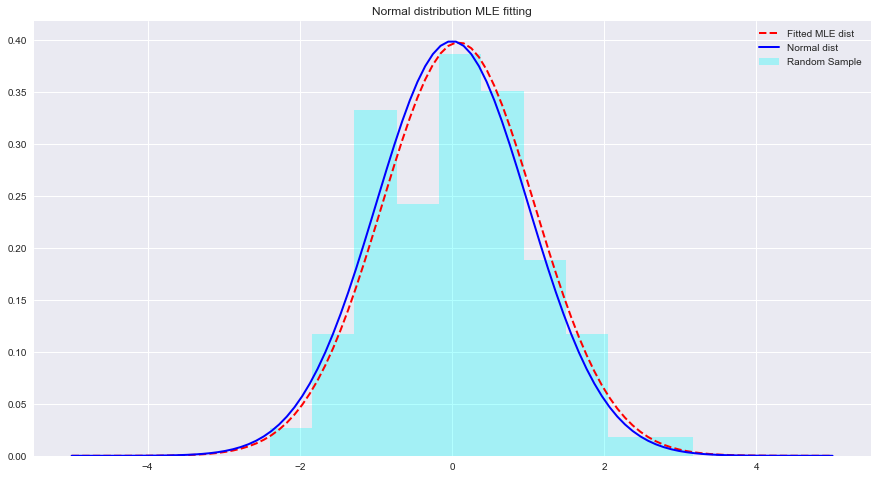

png

 #  Your comments/observations

Ringkasan

Dalam lab singkat ini, kita melihat pengaturan Bayesian dalam konteks Gaussian, yaitu ketika variabel acak yang mendasarinya terdistribusi normal. Kami mempelajari bahwa MLE dapat memperkirakan parameter distribusi normal yang tidak diketahui, dengan memaksimalkan kemungkinan rata-rata yang diharapkan. Rata-rata yang diharapkan mendekati rata-rata distribusi normal yang tidak dilengkapi dalam ruang parameter tersebut. Pemahaman ini akan kita lanjutkan dengan mempelajari bagaimana estimasi tersebut dilakukan dalam memperkirakan sarana sejumlah kelas yang ada dalam distribusi data menggunakan Naive Bayes Classifier.

Memperluas

Informasi Tambahan