Beranda>Terkait pemrograman>Kode sumber lainnya
Unduh

gambar

Struktur Data dan Algoritma dalam JavaScript

Ini adalah implementasi pengkodean buku DSA.js dan repo untuk paket NPM.

Di repositori ini, Anda dapat menemukan implementasi algoritma dan struktur data dalam JavaScript. Materi ini dapat digunakan sebagai panduan referensi bagi pengembang, atau Anda dapat menyegarkan topik tertentu sebelum wawancara. Selain itu, Anda juga dapat menemukan ide untuk memecahkan masalah dengan lebih efisien.

Struktur Data Interaktif

Daftar isi

  • Instalasi
  • Fitur
  • Apa yang ada di dalamnya
    • ? Analisis Algoritma
    • ? Struktur Data Linier
    • ? Struktur Data Non-Linear
    • ⚒ Teknik Algoritma
  • Buku
  • Pertanyaan Umum
  • Mendukung
  • Lisensi

Instalasi

Anda dapat mengkloning repo atau menginstal kode dari NPM: 

npm install dsa.js

dan kemudian Anda dapat mengimpornya ke program atau CLI Anda 

 const { LinkedList , Queue , Stack } = require ( 'dsa.js' ) ;

Untuk daftar semua struktur data dan algoritme yang tersedia, lihat index.js.

Fitur

Algoritma adalah kotak peralatan penting bagi setiap programmer.

Anda perlu memikirkan waktu proses algoritme ketika Anda harus mengurutkan data, mencari nilai dalam kumpulan data besar, mengubah data, menskalakan kode Anda ke banyak pengguna, dan masih banyak lagi. Algoritma hanyalah langkah yang Anda ikuti untuk menyelesaikan masalah, sedangkan struktur data adalah tempat Anda menyimpan data untuk manipulasi nanti. Keduanya digabungkan membuat program.

Algoritma + Struktur Data = Program.

Sebagian besar bahasa pemrograman dan perpustakaan memang menyediakan implementasi untuk struktur data dasar dan algoritma. Namun, untuk memanfaatkan struktur data dengan benar, Anda harus mengetahui pengorbanannya untuk memilih alat terbaik untuk pekerjaan itu.

Materi ini akan mengajarkan Anda untuk:

  • ? Terapkan strategi untuk menjawab pertanyaan algoritma. Jangan pernah terjebak lagi. Selesaikan wawancara itu!
  • ✂️ Bangun algoritma yang efisien. Pelajari cara memecah masalah menjadi bagian-bagian yang bisa ditangani.
  • ? Tingkatkan keterampilan pemecahan masalah Anda dan jadilah pengembang yang berpengalaman dengan memahami konsep dasar ilmu komputer.
  • ? Mencakup topik-topik penting, seperti waktu O yang besar, struktur data, dan algoritma yang harus diketahui. Terapkan 10+ struktur data dari awal.

Apa yang ada di dalamnya

Semua kode dan penjelasan tersedia di repo ini. Anda dapat menggali tautan dan contoh kode dari (folder src). Namun, contoh kode sebaris tidak diperluas (karena keterbatasan asciidoc Github), tetapi Anda dapat mengikuti jalurnya dan melihat implementasinya.

Catatan: Jika Anda lebih suka mengonsumsi informasi secara lebih linier, maka format buku akan lebih sesuai untuk Anda.

Topiknya dibagi menjadi empat kategori utama, seperti yang Anda lihat di bawah:

? Analisis Algoritma

Nugget Ilmu Komputer tanpa semua omong kosong. (Klik untuk memperluas)

Nugget Ilmu Komputer tanpa semua omong kosong

Pelajari cara menghitung waktu proses dari contoh kode

Menerjemahkan baris kode ke perkiraan jumlah operasi

Pelajari cara membandingkan algoritma menggunakan notasi Big O. (Klik untuk memperluas)

Pelajari cara membandingkan algoritma menggunakan notasi Big O.

Membandingkan algoritma menggunakan notasi Big O

Katakanlah Anda ingin mencari duplikat pada sebuah array. Dengan menggunakan notasi Big O, kita dapat membandingkan solusi berbeda yang memecahkan masalah yang sama namun memiliki perbedaan besar dalam waktu yang dibutuhkan untuk menyelesaikannya.

  • Solusi optimal menggunakan peta
  • Menemukan duplikat dalam array (pendekatan naif)
8 contoh untuk dijelaskan dengan kode cara menghitung kompleksitas waktu. (Klik untuk memperluas)

8 contoh untuk dijelaskan dengan kode cara menghitung kompleksitas waktu

Kompleksitas waktu yang paling umum

gambar

Grafik kompleksitas waktu

Kompleksitas waktu yang paling umum

? Struktur Data Linier

Pahami seluk beluk struktur data yang paling umum. (Klik untuk memperluas)

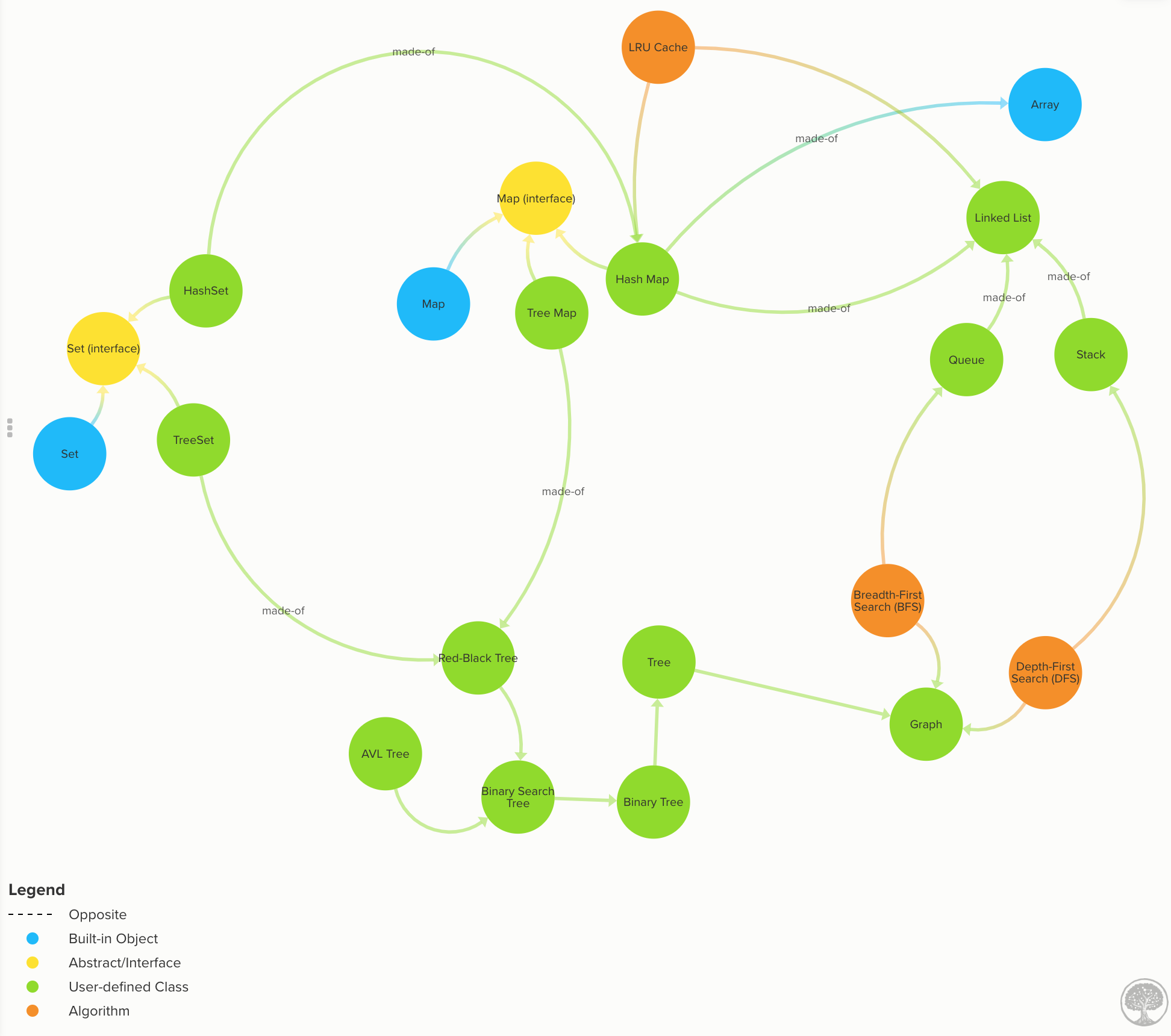
Pahami seluk beluk struktur data yang paling umum

  • Array: Terintegrasi di sebagian besar bahasa sehingga tidak diterapkan di sini. Kompleksitas Waktu Array

  • Daftar Tertaut: setiap node data memiliki tautan ke node berikutnya (dan sebelumnya). Kode | Kompleksitas Waktu Daftar Tertaut

  • Antrian: aliran data dengan cara "masuk pertama, keluar pertama" (FIFO). Kode | Kompleksitas Waktu Antrian

  • Tumpukan: data mengalir dengan cara "masuk terakhir, keluar pertama" (LIFO). Kode | Kompleksitas Waktu Tumpukan

Kapan menggunakan Array atau Linked List. Ketahui pengorbanannya. (Klik untuk memperluas)

Kapan menggunakan Array atau Linked List. Ketahui pengorbanannya

Gunakan Array ketika…

  • Anda perlu mengakses data dalam urutan acak dengan cepat (menggunakan indeks).
  • Data Anda multidimensi (misalnya matriks, tensor).

Gunakan Daftar Tertaut ketika:

  • Anda akan mengakses data Anda secara berurutan.
  • Anda ingin menghemat memori dan hanya mengalokasikan memori sesuai kebutuhan.
  • Anda ingin waktu yang konstan untuk menghapus/menambahkan dari daftar ekstrem.
  • ketika persyaratan ukuran tidak diketahui - keunggulan ukuran dinamis
Buat Daftar, Tumpukan, dan Antrean. (Klik untuk memperluas)

Buat Daftar, Tumpukan, dan Antrean dari awal

Bangun salah satu struktur data berikut dari awal:

  • Daftar Tertaut
  • Tumpukan
  • Antre

? Struktur Data Non-Linear

Pahami salah satu struktur data paling serbaguna: Hash Maps. (Klik untuk memperluas)

Peta Hash

Pelajari cara menerapkan berbagai jenis Maps seperti:

  • Peta Hash
  • Peta Pohon

Pelajari juga perbedaan antara berbagai penerapan Maps:

  • HashMap lebih hemat waktu. TreeMap lebih hemat ruang.
  • Kompleksitas pencarian TreeMap adalah O(log n) , sedangkan HashMap yang dioptimalkan rata-rata adalah O(1) .
  • Kunci HashMap berada dalam urutan penyisipan (atau acak tergantung pada implementasinya). Kunci TreeMap selalu diurutkan.
  • TreeMap menawarkan beberapa data statistik secara gratis seperti: dapatkan minimum, dapatkan maksimum, median, temukan rentang kunci. HashMap tidak.
  • TreeMap selalu memiliki jaminan O(log n) , sedangkan HashMap s memiliki waktu diamortisasi sebesar O(1) tetapi dalam kasus pengulangan yang jarang terjadi, diperlukan O(n) .
Mengetahui sifat-sifat Grafik dan Pohon. (Klik untuk memperluas)

Mengetahui sifat-sifat Grafik dan Pohon

Grafik

Ketahui semua properti grafik dengan banyak gambar dan ilustrasi.

contoh grafik dengan bandara AS

Grafik : node data yang dapat memiliki koneksi atau tepi ke nol atau lebih node yang berdekatan. Tidak seperti pohon, node dapat memiliki banyak orang tua, loop. Kode | Kompleksitas Waktu Grafik

Pohon

Pelajari semua jenis pohon dan sifat-sifatnya.

properti struktur data pohon

  • Pohon : node data memiliki nol atau lebih node yang berdekatan alias anak. Setiap node hanya dapat memiliki satu node induk, sebaliknya merupakan grafik, bukan pohon. Kode | dokumen

    • Pohon Biner : sama seperti pohon tetapi hanya dapat memiliki paling banyak dua anak. Kode | dokumen

    • Pohon Pencarian Biner (BST): sama seperti pohon biner, tetapi nilai node tetap menjaga urutan ini left < parent < right . Kode | Kompleksitas Waktu BST

    • Pohon AVL : BST yang seimbang untuk memaksimalkan waktu pencarian. Kode | Dokumen Pohon AVL | Dokumen penyeimbangan diri & rotasi pohon

    • Pohon Merah-Hitam : BST yang seimbang lebih longgar dibandingkan AVL untuk memaksimalkan kecepatan penyisipan. Kode

Terapkan pohon pencarian biner untuk pencarian cepat.

Terapkan pohon pencarian biner untuk pencarian cepat

  • Pelajari cara menambah/menghapus/memperbarui nilai di pohon: memasukkan simpul ke dalam pohon

  • Bagaimana cara membuat pohon seimbang?

Dari BST tidak seimbang hingga BST seimbang 

 1                           2
                         /   
   2        =>           1     3
    
     3

⚒ Kotak Alat Algoritma

Jangan pernah terjebak memecahkan masalah dengan 7 langkah sederhana. (Klik untuk memperluas)

Jangan pernah terjebak memecahkan masalah dengan 8 langkah sederhana

  1. Pahami masalahnya
  2. Buat contoh sederhana (belum ada kasus edge)
  3. Solusi brainstorming (algoritma serakah, Divide and Conquer, Backtracking, brute force)
  4. Uji jawaban Anda pada contoh sederhana (secara mental)
  5. Optimalkan solusinya
  6. Tulis kode. Ya, sekarang Anda bisa membuat kode.
  7. Uji kode tertulis Anda
  8. Analisis kompleksitasnya, baik ruang maupun waktu, dan pastikan untuk mengoptimalkan lebih lanjut.

Detail selengkapnya di sini

Kuasai algoritma pengurutan paling populer (pengurutan gabungan, pengurutan cepat, dll.) (Klik untuk memperluas)

Kuasai algoritma pengurutan paling populer

Kita akan mengeksplorasi tiga algoritma pengurutan penting O(n^2), yang memiliki overhead rendah:

  • Sortir Gelembung. Kode | dokumen

  • Sortir Penyisipan. Kode | dokumen

  • Sortir Seleksi. Kode | dokumen

dan kemudian mendiskusikan algoritma pengurutan yang efisien O(n log n) seperti:

  • Gabungkan Sortir. Kode | dokumen

  • Sortir cepat. Kode | dokumen

Pelajari berbagai pendekatan untuk memecahkan masalah seperti membagi dan menaklukkan, pemrograman dinamis, algoritma serakah, dan kemunduran. (Klik untuk memperluas)

Pelajari berbagai pendekatan untuk memecahkan masalah algoritmik

Kita akan membahas teknik berikut untuk menyelesaikan masalah algoritma:

  • Algoritma Greedy: membuat pilihan serakah menggunakan heuristik untuk menemukan solusi terbaik tanpa melihat ke belakang.
  • Pemrograman Dinamis: teknik untuk mempercepat algoritma rekursif ketika terdapat banyak submasalah yang tumpang tindih . Ini menggunakan memoisasi untuk menghindari duplikasi pekerjaan.
  • Divide and Conquer (Membagi dan Menaklukkan): membagi masalah menjadi bagian-bagian yang lebih kecil, menaklukkan setiap submasalah, dan kemudian menggabungkan hasilnya.
  • Backtracking: mencari semua (atau beberapa) jalur yang mungkin. Namun, ini berhenti, dan kembali lagi segera setelah menyadari bahwa solusi saat ini tidak berfungsi.
  • Brute Force : menghasilkan semua solusi yang mungkin dan mencoba semuanya. (Gunakan ini sebagai pilihan terakhir atau sebagai titik awal).

Pertanyaan Umum

Bagaimana saya menerapkannya dalam pekerjaan saya sehari-hari? (Klik untuk memperluas)

Sebagai seorang programmer, kita harus menyelesaikan masalah setiap hari. Jika Anda ingin menyelesaikan masalah dengan baik, ada baiknya mengetahui berbagai macam solusi. Seringkali, mempelajari sumber daya yang ada lebih efisien daripada menemukan jawabannya sendiri. Semakin banyak alat dan latihan yang Anda miliki, semakin baik. Buku ini membantu Anda memahami trade-off antara struktur data dan alasan tentang kinerja algoritma.

Mengapa Anda membuat repo/buku ini?

Tidak banyak buku tentang Algoritma dalam JavaScript. Bahan ini mengisi kekosongan tersebut. Juga, ini latihan yang bagus :)

Apakah ada orang yang dapat saya hubungi jika saya memiliki pertanyaan tentang sesuatu yang khusus?

Ya, buka terbitan atau ajukan pertanyaan di [slack channel](https://dsajs-slackin.herokuapp.com).

Buku

Proyek ini juga tersedia dalam sebuah buku. Anda akan mendapatkan PDF yang diformat dengan baik dengan 180+ halaman + versi ePub dan Mobi.

Mendukung

Hubungi saya di salah satu tempat berikut!

  • Twitter di @iAmAdrianMejia
  • Ngobrol di dsajs.slack.com

Lisensi

Memperluas
Informasi Tambahan
Aplikasi Terkait
Direkomendasikan untuk Anda
Informasi Terkait Semua