Memecahkan teka-teki Menara Hanoi dengan pembelajaran penguatan.
Di lingkungan Python dengan Numpy dan Pandas terinstal, jalankan skrip hanoi.py untuk menghasilkan tiga plot yang ditampilkan di bagian Hasil. Script dapat dengan mudah diadaptasi untuk memainkan game dengan jumlah disk N yang berbeda, misalnya.
Pembelajaran penguatan baru-baru ini mendapat minat baru dengan pemukulan pemain Go manusia profesional oleh AlphaGo Google Deepmind. Di sini, teka-teki yang lebih sederhana terpecahkan: permainan Menara Hanoi. Implementasinya mengikuti algoritma Q-learning seperti yang dikemukakan oleh Watkins & Dayan [1].
Permainan Tower of Hanoi terdiri dari tiga pasak dan sejumlah piringan dengan ukuran berbeda yang dapat digeser ke pasak tersebut. Teka-teki dimulai dengan semua disk ditumpuk pada pasak pertama dalam urutan menaik, dengan yang terbesar di bawah dan yang terkecil di atas. Tujuan permainan ini adalah memindahkan semua disk ke pasak ketiga. Satu-satunya perpindahan yang sah adalah memindahkan disk paling atas dari satu pasak ke pasak lainnya, dengan batasan bahwa disk tidak boleh ditempatkan pada disk yang lebih kecil. Gambar 1 menunjukkan solusi optimal untuk 4 disk.

Gambar 1. Solusi animasi teka-teki Menara Hanoi untuk 4 disk. (Sumber: Wikipedia).
Mengikuti Anderson [2], kami mewakili keadaan permainan dengan tupel, di mana elemen ke -i menunjukkan pada pasak mana disk ke -i berada. Disk diberi label berdasarkan ukuran yang bertambah. Jadi, keadaan awal adalah (111), dan keadaan akhir yang diinginkan adalah (333) (Gambar 2).
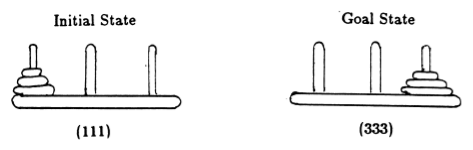
Gambar 2. Keadaan awal dan tujuan teka-teki Menara Hanoi dengan 3 disk. (Dari [2]).
Keadaan teka-teki dan transisi di antara mereka sesuai dengan gerakan hukum membentuk grafik transisi keadaan teka-teki, yang ditunjukkan pada Gambar 3.
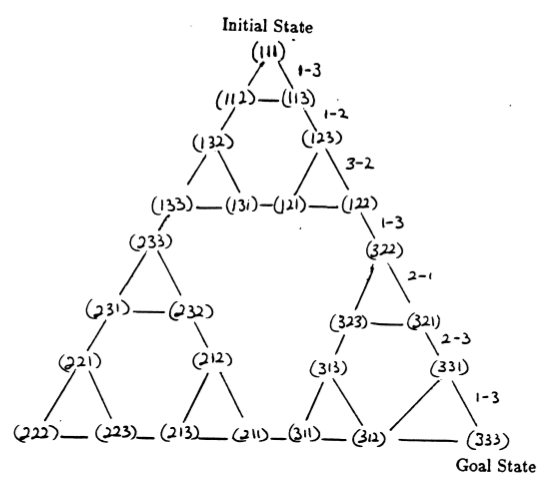
Gambar 3. Nyatakan grafik transisi untuk teka-teki Menara Hanoi tiga disk (di atas) dan solusi 7 langkah optimal yang sesuai (di bawah), yang mengikuti jalur di sisi kanan grafik. (Dari [2] dan Mathforum.org).
Jumlah gerakan minimum yang diperlukan untuk memecahkan teka-teki Menara Hanoi adalah 2 N - 1, dimana N adalah jumlah disk. Jadi untuk N = 3, teka-teki tersebut dapat diselesaikan dalam 7 langkah, seperti yang ditunjukkan pada Gambar 3. Pada bagian berikut, kami menguraikan bagaimana hal ini dicapai dengan Q-learning.
R dan matriks 'nilai tindakan' Q untuk 2 disk Langkah pertama dalam program ini adalah menghasilkan matriks imbalan R yang menangkap aturan permainan dan memberikan imbalan bagi yang memenangkannya. Untuk mempermudah, matriks reward ditunjukkan untuk N = 2 disk pada Gambar 4.
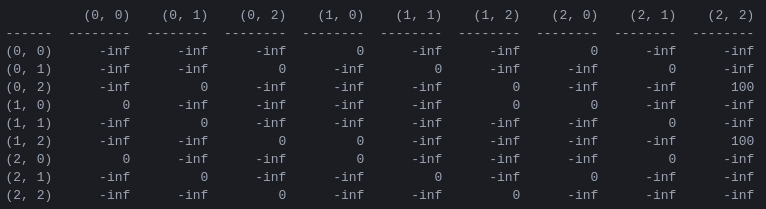
Gambar 4. Matriks hadiah R untuk teka-teki Menara Hanoi dengan N = 2 disk. Elemen ( i , j ) mewakili hadiah untuk berpindah dari keadaan i ke j . Negara bagian diberi label oleh tupel seperti pada Gambar 2 dan 3, dengan perbedaan bahwa pasak diindeks 'secara pythononik' dari 0 ke 2, bukan dari 1 ke 3. Pergerakan yang mengarah ke keadaan tujuan (2,2) diberi hadiah dari 100, gerakan ilegal sebesar , dan semua gerakan lainnya sebesar 0.
Matriks imbalan R hanya menjelaskan imbalan langsung : imbalan 100 hanya dapat dicapai dari keadaan kedua dari belakang (0,2) dan (1,2). Di negara bagian lain, masing-masing dari 2 atau 3 kemungkinan gerakan memiliki imbalan yang sama sebesar 0, dan tidak ada alasan yang jelas untuk memilih salah satu dari yang lain.
Pada akhirnya, kami berusaha untuk memberikan 'nilai' pada setiap kemungkinan pergerakan di setiap negara bagian, sehingga dengan memaksimalkan nilai-nilai ini kami dapat menentukan kebijakan yang mengarah pada solusi optimal. Matriks 'nilai' untuk setiap tindakan di setiap keadaan disebut Q dan dapat diselesaikan secara rekursif, atau 'dipelajari', dengan cara stokastik seperti yang dijelaskan oleh Watkins & Dayan [1]. Hasil untuk 2 disk ditunjukkan pada Gambar 5.
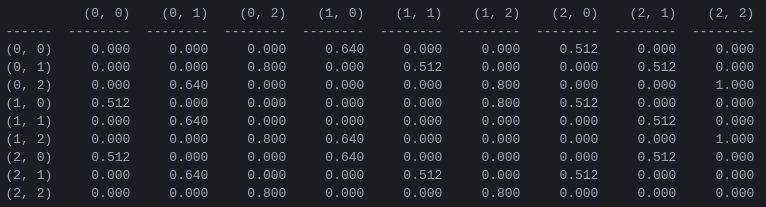
Gambar 5. Matriks 'Nilai tindakan' Q untuk game Tower of Hanoi dengan 2 disk, dipelajari dengan faktor diskon = 0,8, faktor pembelajaran = 1,0, dan 1000 episode pelatihan.
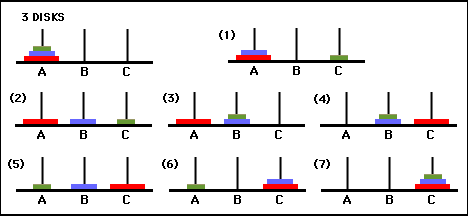
Nilai-nilai matriks Q pada dasarnya adalah bobot yang dapat ditetapkan ke simpul-simpul grafik transisi keadaan pada Gambar 3, yang memandu agen dari keadaan awal ke keadaan tujuan dengan cara sesingkat mungkin. Dalam contoh ini, dengan memulai dari keadaan (0,0) dan secara berturut-turut memilih pergerakan dengan nilai Q tertinggi, pembaca dapat meyakinkan dirinya sendiri bahwa matriks Q mengarahkan agen melalui urutan keadaan (0,0) - (1 ,0) - (1,2) - (2,2), yang sesuai dengan solusi optimal 3 langkah dari game Tower of Hanoi 2 disk (Gambar 6).
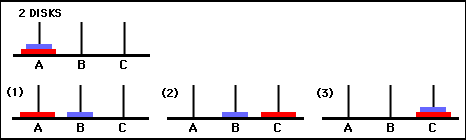
Gambar 6. Solusi game Tower of Hanoi dengan 2 disk. Keadaan yang berurutan masing-masing diwakili oleh (0,0), (1,0), (1,2), dan (2,2). (Sumber: mathforum.org).
Dalam contoh ini, ketika matriks Q telah menyatu ke nilai optimalnya, matriks ini mendefinisikan kebijakan stasioner : setiap baris berisi satu tindakan dengan nilai maksimum yang unik. Namun, selama proses pembelajaran, tindakan yang berbeda mungkin memiliki nilai Q yang sama. (Khususnya, hal ini terjadi pada awal pelatihan ketika Q diinisialisasi ke matriks nol). Dalam simulasi yang disajikan di bagian berikut, situasi seperti ini ditangani oleh kebijakan stokastik berikut: dalam kasus di mana nilai Q maksimum dibagi di antara beberapa tindakan, pilih salah satu dari tindakan ini secara acak.
Kinerja algoritma Q-learning dapat diukur dengan menghitung jumlah gerakan yang diperlukan (rata-rata) untuk memecahkan teka-teki Menara Hanoi. Jumlah ini berkurang seiring dengan banyaknya episode pelatihan hingga akhirnya mencapai nilai optimum 2 N - 1, dimana N adalah jumlah disk, seperti diilustrasikan pada Gambar 7 untuk N = 2, 3, dan 4.
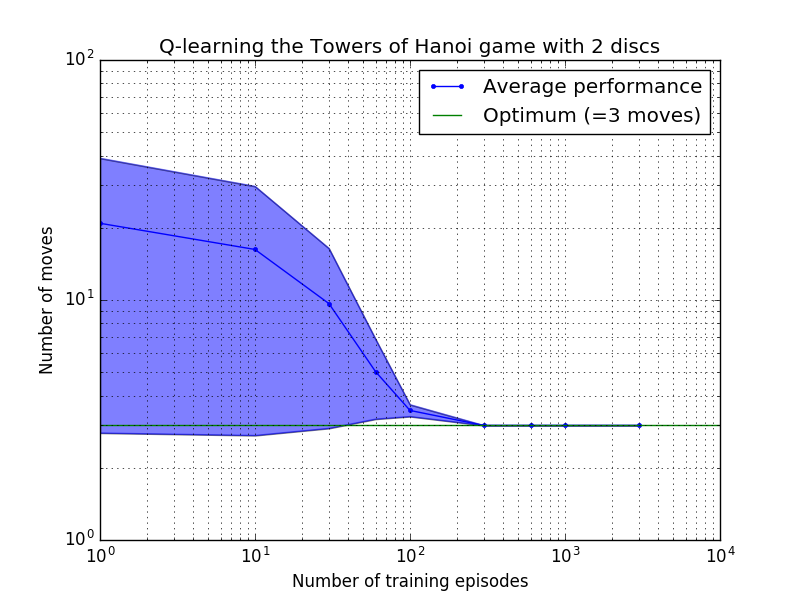
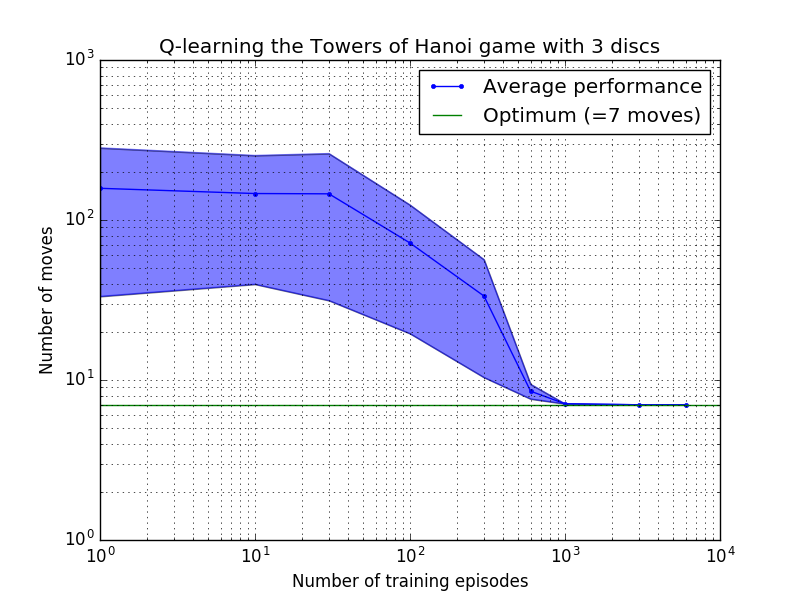
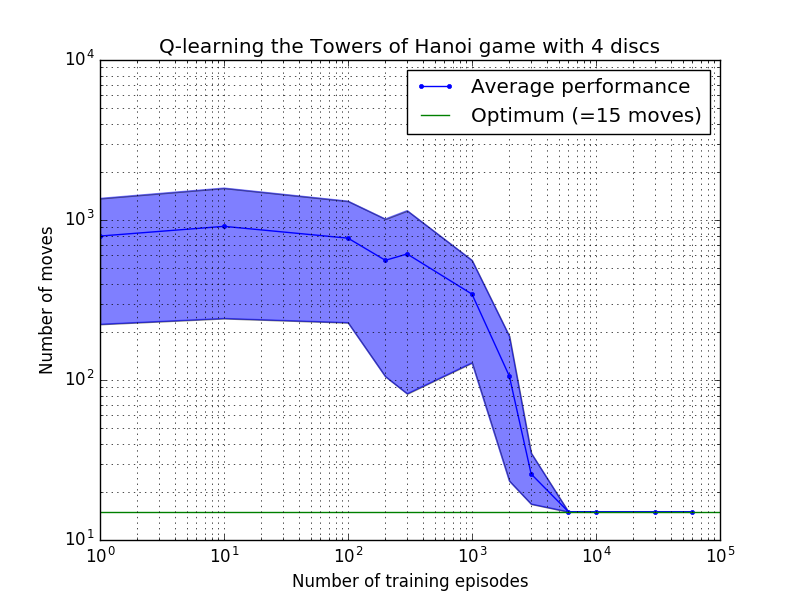
Gambar 7. Kinerja algoritma Q-learning untuk game Tower of Hanoi dengan, dari atas ke bawah, 2, 3, dan 4 disk. Dalam semua kasus, pembelajaran dilakukan dengan faktor diskon = 0,8 dan faktor pembelajaran = 1,0. Kurva biru solid mewakili kinerja rata-rata selama 100 periode pelatihan dan bermain game 100 kali untuk setiap kebijakan stokastik yang dihasilkan. Batas atas dan bawah area biru yang diarsir diimbangi dari rata-rata dengan perkiraan deviasi standar. (Untuk N = 3 dan N = 4, jumlah episode pelatihan dan waktu bermain masing-masing dikurangi menjadi 10 dan 10, karena kendala komputasi).
Fitur yang menarik dari karakteristik pembelajaran pada Gambar 7 adalah bahwa dalam semua kasus, pembelajaran pada awalnya lambat, dan agen hampir tidak memberikan hasil yang lebih baik daripada kebijakan 'tanpa pelatihan' yang memilih gerakan secara acak. Pada titik tertentu, pembelajaran mencapai 'titik belok' dan kemudian menyatu ke jumlah gerakan optimal dengan kecepatan yang dipercepat (walaupun hal ini agak dilebih-lebihkan oleh skala logaritmik).
Skrip Python berhasil memecahkan teka-teki Menara Hanoi secara optimal untuk sejumlah disk dengan Q-learning. Skrip dapat dengan mudah disesuaikan dengan masalah lain dengan matriks imbalan yang berbeda R .
Jumlah episode pelatihan yang diperlukan untuk menyatu ke solusi optimal meningkat pesat seiring dengan jumlah disk N : untuk N=2 disk diperlukan ~300 episode, sedangkan untuk N=4 diperlukan ~6.000. Peningkatan yang mungkin dilakukan pada algoritma pembelajaran adalah memungkinkan algoritma tersebut secara otomatis mencari solusi rekursif, seperti yang dilakukan oleh Hengst [3].
[1] Watkins & Dayan, Q-learning , Pembelajaran Mesin, 8, 279-292 (1992). (PDF).
[2] Anderson, Pembelajaran dan Pemecahan Masalah dengan Sistem Koneksi Multilayer , Ph.D. tesis (1986). (PDF).
[ 3 ] Hengst, Menemukan Hierarki dalam Pembelajaran Penguatan dengan HEXQ , Prosiding Konferensi Internasional Kesembilan Belas tentang Pembelajaran Mesin (2002). (PDF).