Balikkan matriks menggunakan jaringan saraf.
Pembalik matriks menghadirkan tantangan unik untuk jaringan saraf, terutama karena keterbatasan yang melekat dalam melakukan operasi aritmatika yang tepat seperti perkalian dan pembagian pada aktivasi. Jaringan padat tradisional sering kali membutuhkan bantuan dengan tugas -tugas ini, karena mereka tidak dirancang secara eksplisit untuk menangani kompleksitas yang terlibat dalam inversi matriks. Eksperimen yang dilakukan dengan jaringan saraf padat sederhana telah menunjukkan kesulitan yang signifikan mencapai inversi matriks yang akurat. Terlepas dari berbagai upaya untuk mengoptimalkan proses arsitektur dan pelatihan, hasilnya sering membutuhkan peningkatan. Namun, beralih ke arsitektur yang lebih kompleks-jaringan residu 7-lapis (ResNet)-dapat menyebabkan peningkatan kinerja yang nyata.
Arsitektur ResNet, yang dikenal karena kemampuannya untuk mempelajari representasi mendalam melalui koneksi residual, telah terbukti efektif dalam mengatasi inversi matriks. Dengan jutaan parameter, jaringan ini dapat menangkap pola rumit dalam data yang tidak bisa dilakukan oleh model yang lebih sederhana. Namun, kompleksitas ini datang dengan biaya: Data pelatihan substansial diperlukan untuk generalisasi yang efektif.
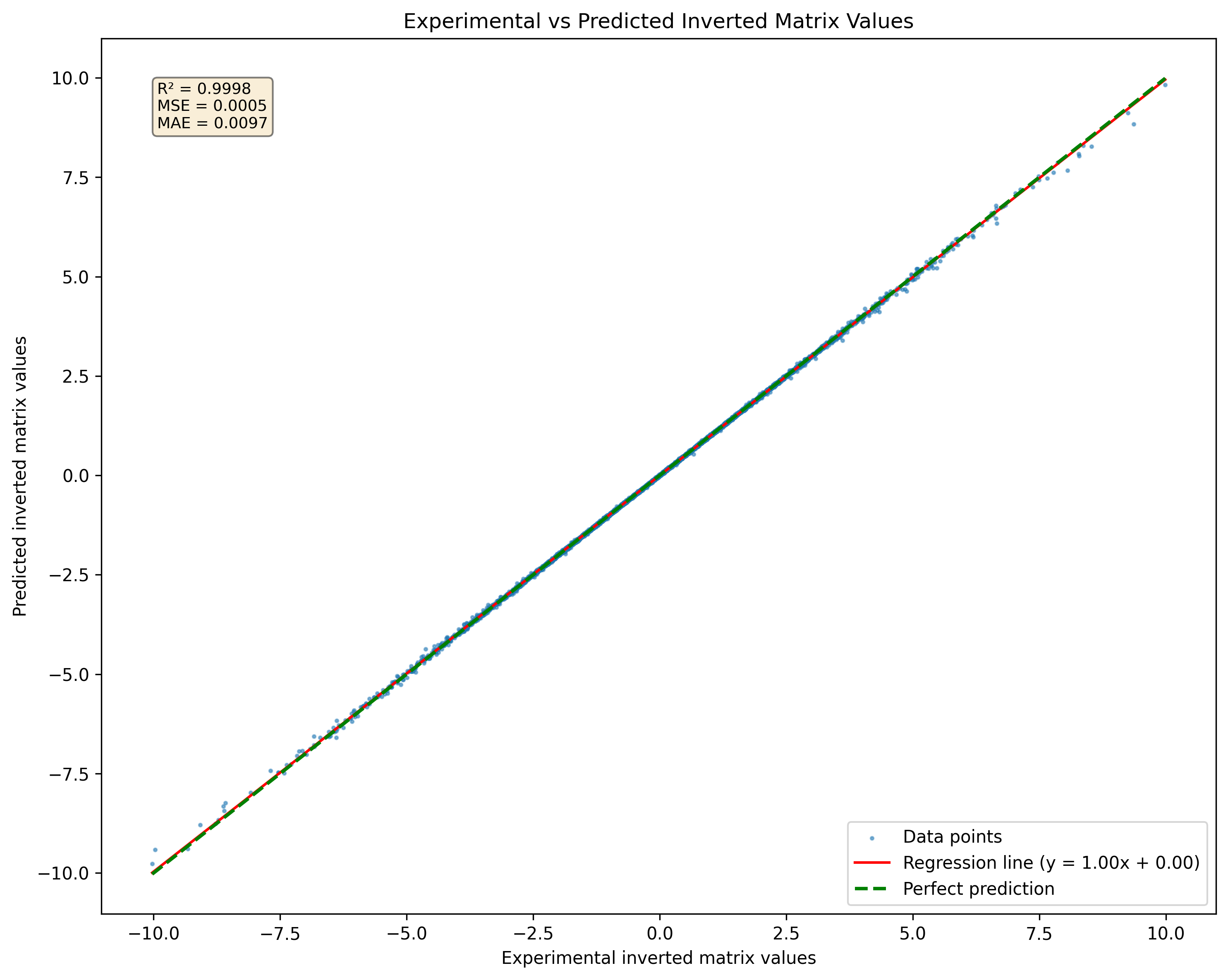Gambar 1: Visualisasi jaringan saraf yang diprediksi matriks terbalik untuk satu set matriks 3x3 tidak pernah terlihat dalam dataset
Untuk mengevaluasi kinerja jaringan saraf dalam memprediksi inversi matriks, fungsi kerugian spesifik digunakan:
Dalam persamaan ini:
Tujuannya adalah untuk meminimalkan perbedaan antara matriks identitas dan produk dari matriks asli dan kebalikannya yang diprediksi. Fungsi kerugian ini secara efektif mengukur seberapa dekat terbalik yang diprediksi menjadi akurat.
Selain itu, jika
Fungsi kerugian ini menawarkan keunggulan berbeda dibandingkan fungsi kerugian tradisional seperti rata -rata kesalahan kuadrat (MSE) atau kesalahan absolut rata -rata (MAE).
Pengukuran langsung dari akurasi inversi Tujuan utama inversi matriks adalah untuk memastikan bahwa produk dari suatu matriks dan kebalikannya menghasilkan matriks identitas. Fungsi kerugian secara langsung menangkap persyaratan ini dengan mengukur penyimpangan dari matriks identitas. Sebaliknya, MSE dan MAE fokus pada perbedaan antara nilai -nilai yang diprediksi dan nilai -nilai yang benar tanpa secara eksplisit membahas properti mendasar dari inversi matriks.
Penekanan pada integritas struktural dengan menggunakan fungsi kerugian yang mengevaluasi seberapa dekat produk AA - 1AA - 1 dengan II, ia menekankan mempertahankan integritas struktural matriks yang terlibat. Ini sangat penting dalam aplikasi di mana menjaga hubungan linier sangat penting. Fungsi kerugian tradisional seperti MSE dan MAE tidak memperhitungkan aspek struktural ini, yang berpotensi mengarah pada solusi yang meminimalkan kesalahan tetapi gagal memenuhi persyaratan matematika dari inversi matriks.
Penerapan pada matriks non-singular fungsi kerugian ini secara inheren mengasumsikan bahwa matriks yang terbalik adalah non-singular (yaitu, secara tidak dapat dibalik). Dalam skenario di mana matriks tunggal hadir, fungsi kerugian tradisional mungkin menghasilkan hasil yang menyesatkan karena mereka tidak memperhitungkan ketidakmungkinan mendapatkan kebalikan yang valid. Fungsi kerugian yang diusulkan menyoroti batasan ini dengan menghasilkan kesalahan yang lebih besar ketika mencoba membalikkan matriks tunggal.
Salah satu batasan yang signifikan saat menggunakan jaringan saraf untuk inversi matriks adalah ketidakmampuan mereka untuk menangani matriks tunggal secara efektif. Matriks tunggal tidak memiliki kebalikan; Dengan demikian, setiap upaya oleh jaringan saraf untuk memprediksi kebalikan untuk matriks tersebut akan menghasilkan hasil yang salah. Dalam praktiknya, jika matriks tunggal disajikan selama pelatihan atau inferensi, jaringan mungkin masih menghasilkan hasil, tetapi output ini tidak akan valid atau bermakna. Keterbatasan ini menggarisbawahi pentingnya memastikan bahwa data pelatihan terdiri dari matriks non-singular bila memungkinkan.
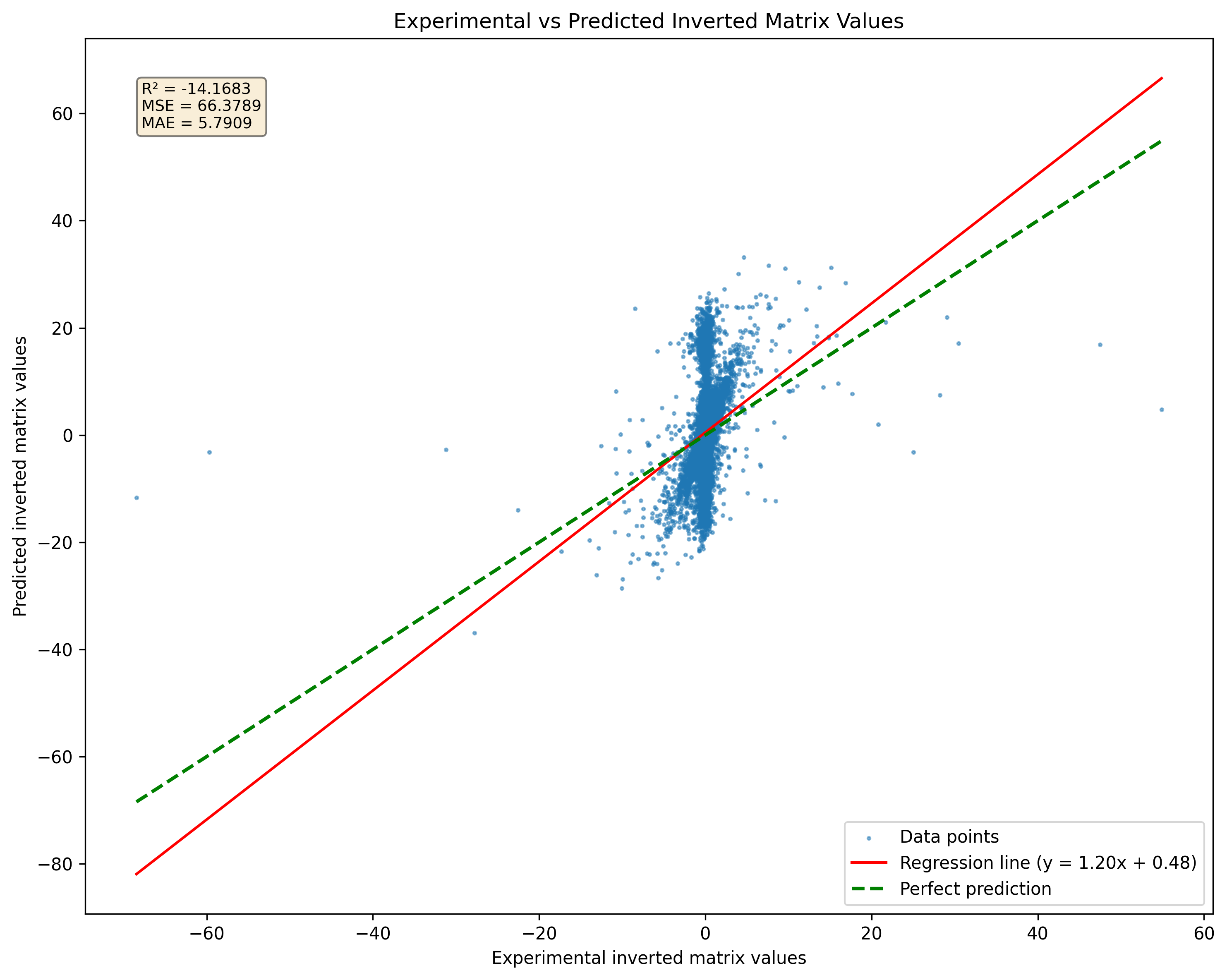Gambar 2: Perbandingan prediksi model untuk matriks tunggal versus pseudoinversions. Perhatikan bahwa model akan menghasilkan hasil terlepas dari singularitas matriks.
Penelitian menunjukkan bahwa model resnet dapat menghafal sejumlah sampel yang baik tanpa kehilangan akurasi yang signifikan. Namun, meningkatkan ukuran dataset menjadi 10 juta sampel dapat menyebabkan overfiting yang parah. Overfitting ini terjadi meskipun volume data yang besar, menyoroti bahwa hanya meningkatkan ukuran dataset tidak menjamin peningkatan generalisasi untuk model kompleks. Untuk mengatasi tantangan ini, strategi pembuatan data yang berkelanjutan dapat diadopsi. Alih -alih mengandalkan dataset statis, sampel dapat dihasilkan dengan cepat dan diumpankan ke jaringan saat dibuat. Pendekatan ini, yang sangat penting dalam mengurangi overfitting, tidak hanya memberikan beragam contoh pelatihan tetapi juga memastikan bahwa model tersebut terpapar pada dataset yang terus berkembang.
Singkatnya, sementara inversi matriks secara inheren menantang untuk jaringan saraf karena keterbatasan dalam operasi aritmatika, memanfaatkan arsitektur canggih seperti ResNet dapat menghasilkan hasil yang lebih baik. Namun, pertimbangan yang cermat harus diberikan pada persyaratan data dan risiko overfitting. Sampel pelatihan yang terus -menerus menghasilkan dapat meningkatkan proses pembelajaran model dan meningkatkan kinerja dalam tugas inversi matriks. Versi ini mempertahankan nada impersonal saat membahas tantangan dan strategi dalam melatih jaringan saraf untuk inversi matriks.
DeepMatrixInversion didistribusikan di bawah lisensi LGPLV3
Untuk mengetahui lebih lanjut secara detail bagaimana lisensi berfungsi, silakan baca file "lisensi" atau buka "http://www.gnu.org/licenses/lgpl-3.0.html"
DeepMatrixInversion saat ini milik Giuseppe Marco Randazzo.
Untuk memasang repositori DeepMatrixInversion, Anda dapat memilih antara menggunakan puisi, PIP atau PIPX di bawah ini adalah instruksi untuk kedua metode.
git clone https://github.com/gmrandazzo/DeepMatrixInversion.git
cd DeepMatrixInversion
python3 -m venv .venv
. .venv/bin/activate
pip install poetry
poetry install
Ini akan mengatur lingkungan Anda dengan semua paket yang diperlukan untuk menjalankan DeepMatrixInversion.
Buat lingkungan virtual dan instal DeppMatrixInversion dengan PIP
python3 -m venv .venv
. .venv/bin/activate
pip install git+https://github.com/gmrandazzo/DeepMatrixInversion.git
Jika Anda lebih suka menggunakan PIPX, yang memungkinkan Anda memasang aplikasi Python di lingkungan yang terisolasi, ikuti langkah -langkah ini:
python3 -m pip install --user pipx
apt-get install pipx
brew install pipx
sudo dnf install pipx
Pipx Instal Git+https: //github.com/gmrandazzo/deepmatrixInversion.git
Untuk melatih model yang dapat melakukan inversi matriks, Anda akan menggunakan perintah DMXTrain. Perintah ini memungkinkan Anda untuk menentukan berbagai parameter yang mengontrol proses pelatihan, seperti ukuran matriks, kisaran nilai, dan durasi pelatihan.
dmxtrain --msize < matrix_size > --rmin < min_value > --rmax < max_value > --epochs < number_of_epochs > --batch_size < size_of_batches > --n_repeats < number_of_repeats > --mout < output_model_path > dmxtrain --msize --rmin -1 --rmax 1 --epochs 5000 --batch_size 1024 --n_repeats 3 --mout ./Model_3x3
--msize <matrix_size>: Specifies the size of the square matrices to be generated for training. For example, 3 for 3x3 matrices.
--rmin <min_value>: Sets the minimum value for the random elements in the matrices. For instance, -1 will allow negative values.
--rmax <max_value>: Sets the maximum value for the random elements in the matrices. For example, 1 will limit values to a maximum of 1.
--epochs <number_of_epochs>: Defines how many epochs (complete passes through the training dataset) to run during training. A higher number typically leads to better performance; in this case, 5000.
--batch_size <size_of_batches>: Determines how many samples are processed before the model is updated. A batch size of 1024 means that 1024 samples are used in each iteration.
--n_repeats <number_of_repeats>: Indicates how many times to repeat the training process with different random seeds or initializations. This can help ensure robustness; for instance, repeating 3 times.
--mout <output_model_path>: Specifies where to save the trained model. In this example, it saves to ./Model_3x3.
Setelah Anda melatih model Anda, Anda dapat menggunakannya untuk melakukan inversi matriks pada matriks input baru. Perintah untuk inferensi adalah DMXInvert, yang mengambil matriks input dan mengeluarkan kebalikannya.
Peringatan: DMXInvert dapat membalikkan matriks yang lebih besar dari yang digunakan untuk melatih model melalui rumus inversi blok matriks Sherman-Morrison-Woodbury. Fitur ini hanya berfungsi dengan matriks yang ukuran bloknya dapat dibagi dengan ukuran blok pelatihan model tanpa pengingat. Fitur ini sangat eksperimental dan mungkin perlu direvisi.
dmxinvert --inputmx <input_matrix_file> --inverseout <output_csv_file> --model <model_path>
dmxinvert --inputmx input_matrix.csv --inverseout output_inverse.csv --model ./Model_3x3_*
--inputmx <input_matrix_file>: Specifies the path to the input matrix file that you want to invert. This file should contain a valid matrix format (e.g., CSV).
--inverseout <output_csv_file>: Indicates where to save the resulting inverted matrix. The output will be saved in CSV format.
--model <model_path>: Provides the path to the trained model that will be used for performing the inversion.
Menghasilkan dataset buatan dengan matriks input dan output terbalik dilakukan dengan dmx dmxdatasetgenerator
dmxdatasetgenerator 3 10 -1 1 test_3x3_range_-1+1
Ini akan menghasilkan 10 matriks ukuran 3x3 dengan angka dalam kisaran dari -1 hingga +1.
dmxdatasetgenerator [matrix size] [number of samples] [range min] [range max] [outname_prefix]
Kemudian dataset dapat divalidasi menggunakan DMXDatasetverify
dmxdatasetverify test_3x3_range_-1+1_matrices_3x3.mx test_3x3_range_-1+1_matrices_inverted_3x3.mx invertible
Dataset valid.
dmxdatasetverify [dataset matrix to invert] [dataset matrix inverted] [type: invertible or singular]
File matriks input harus diformat sebagai berikut:
0.24077047370124594,-0.5012474139608847,-0.5409542929032876
-0.6257864520097793,-0.030705148203584942,-0.13723920334288975
-0.48095686716222064,0.19220406568380666,-0.34750000491973854
END
0.4575368007107925,0.9627977617090073,-0.4115240560547333
0.5191433428806012,0.9391491187187144,-0.000952683255491138
-0.17757763984424968,-0.7696584771443977,-0.9619759413623306
END
-0.49823271153034154,0.31993947803488587,0.9380291202366384
0.443652116558352,0.16745965310481048,-0.267270356721347
0.7075720067281346,-0.3310912886946993,-0.12013367141105102
END
Setiap blok angka mewakili matriks terpisah yang diikuti oleh penanda akhir yang menunjukkan akhir dari matriks itu.
