Dalam beberapa tahun terakhir, model bahasa besar (LLM) telah menunjukkan kemampuan luar biasa di berbagai bidang, namun kemampuan penalaran matematisnya ternyata sangat lemah. Editor Downcodes akan menafsirkan studi terbaru untuk Anda, yang mengungkapkan "rahasia" LLM yang luar biasa dalam operasi aritmatika, dan menganalisis keterbatasan metode ini dan arah perbaikan di masa depan. Penelitian ini tidak hanya memperdalam pemahaman kita tentang mekanisme operasi internal LLM, tetapi juga memberikan referensi berharga untuk meningkatkan kemampuan matematika LLM.
Baru-baru ini, model bahasa besar AI (LLM) telah bekerja dengan baik dalam berbagai tugas, termasuk menulis puisi, menulis kode, dan mengobrol. Mereka mahakuasa! Tapi, percayakah Anda? AI "jenius" ini sebenarnya adalah " Pemula matematika! Mereka sering kali terbalik ketika memecahkan masalah aritmatika sederhana, dan ini mengejutkan.
Sebuah studi terbaru telah mengungkap rahasia "aneh" di balik kemampuan penalaran aritmatika LLM: mereka tidak mengandalkan algoritma atau memori yang kuat, tetapi mengadopsi strategi yang disebut "gado-gado heuristik"! Ini seperti siswa yang tidak mempelajari rumus dan teorema matematika dengan serius, tetapi bergantung pada "sedikit kepintaran" dan "aturan praktis" untuk mendapatkan jawabannya.
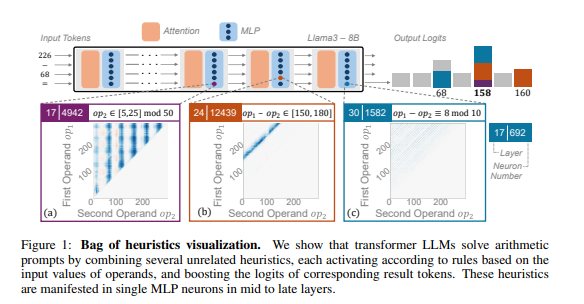
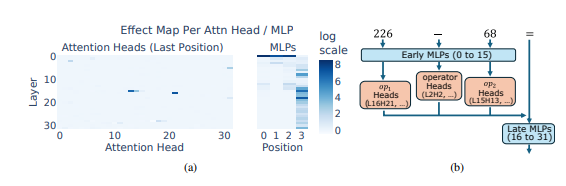
Para peneliti menggunakan penalaran aritmatika sebagai tugas khas dan melakukan analisis mendalam terhadap beberapa LLM seperti Llama3, Pythia dan GPT-J. Mereka menemukan bahwa bagian dari model LLM yang bertanggung jawab untuk perhitungan aritmatika (disebut "rangkaian") terdiri dari banyak neuron individu, yang masing-masing bertindak seperti "kalkulator mini" dan hanya bertanggung jawab untuk mengenali pola numerik tertentu dan mengeluarkan output yang sesuai. menjawab. Misalnya, satu neuron mungkin bertanggung jawab untuk mengidentifikasi "angka yang digit tunggalnya adalah 8", sementara neuron lain mungkin bertanggung jawab untuk mengidentifikasi "operasi pengurangan yang hasilnya antara 150 dan 180".
"Kalkulator mini" ini seperti alat yang campur aduk, dan alih-alih menggunakannya berdasarkan algoritma tertentu, LLM menggunakan kombinasi acak dari "alat" ini untuk menghitung jawaban berdasarkan pola angka yang dimasukkannya. Ibarat seorang chef yang tidak memiliki resep tetap, namun mencampurkannya sesuka hati berdasarkan bahan-bahan yang tersedia, hingga akhirnya menghasilkan “masakan gelap”.
Yang lebih mengejutkan lagi adalah bahwa strategi "gado-gado heuristik" ini sebenarnya muncul pada tahap awal pelatihan LLM dan secara bertahap ditingkatkan seiring dengan kemajuan pelatihan. Ini berarti bahwa LLM mengandalkan pendekatan “tambal sulam” ini sejak awal, dibandingkan mengembangkan strategi ini pada tahap selanjutnya.
Jadi, masalah apa yang akan ditimbulkan oleh metode penalaran aritmatika yang “aneh” ini? Para peneliti menemukan bahwa strategi “gado-gado heuristik” memiliki kemampuan generalisasi yang terbatas dan rentan terhadap kesalahan. Hal ini karena LLM memiliki jumlah "kepintaran kecil" yang terbatas, dan "kepintaran kecil" ini sendiri mungkin juga memiliki kekurangan yang menghalangi mereka untuk memberikan jawaban yang benar ketika menghadapi pola numerik baru. Ibarat seorang chef yang hanya bisa membuat "telur orak-arik tomat", jika tiba-tiba diminta membuat "babi suwir rasa ikan", pasti dia akan terburu-buru dan kebingungan.
Penelitian ini mengungkap keterbatasan kemampuan penalaran aritmatika LLM dan juga menunjukkan arah peningkatan kemampuan matematika LLM di masa depan. Para peneliti percaya bahwa hanya mengandalkan metode pelatihan dan arsitektur model yang ada mungkin tidak cukup untuk meningkatkan kemampuan penalaran aritmatika LLM, dan metode baru perlu dieksplorasi untuk membantu LLM mempelajari algoritma yang lebih kuat dan umum sehingga mereka benar-benar dapat menjadi "master matematika".
Alamat makalah: https://arxiv.org/pdf/2410.21272
Secara keseluruhan, penelitian ini memberikan analisis mendalam tentang strategi "aneh" LLM dalam penalaran matematika, memberikan perspektif baru bagi kita untuk memahami keterbatasan LLM, dan menunjukkan arah penelitian di masa depan. Saya yakin dengan terus berkembangnya teknologi, kemampuan matematika LLM akan meningkat secara signifikan.