

FRKパッケージは CRAN で入手できます。インストールするには、次のように入力してください
install.packages( " FRK " )最新の開発バージョンをインストールするには、 devtoolsロードして次のように入力してください。
install_github( " andrewzm/FRK " , dependencies = TRUE , build_vignettes = TRUE )パッケージを紹介するペーパーはこちらからご覧いただけます。非ガウス設定でのアプローチの詳細を説明した論文は、ここから入手できます (この論文の 6 ページの要約はここから入手できます)。
ビネット「FRK_intro」はパッケージを要約し、ガウス設定で使用できる EM アルゴリズムの詳細を示し、いくつかの例を示します。別のビネット「FRK_non-Gaussian」では、非ガウス設定 (ラプラス近似が使用される) での推論が要約されており、非ガウス データと新しく利用可能なプロット方法を使用した例が含まれています。ビネットにアクセスするには、次のリンクをクリックしてください。
FRKの紹介
FRK を使用した空間および時空間非ガウス データのモデリングに関するチュートリアル
pkgdownページもここから入手できます。
仕事、研究、その他の活動でFRK使用する場合は、 citation("FRK")によって提供される情報を使用して引用してください。
パッケージ: FRK
タイプ: パッケージ
タイトル: 固定ランクのクリギング
バージョン: 2.3.1
日付: 2024-07-16
著者: アンドリュー ザミット マンギオン、マシュー セインズベリー デール
管理者: Andrew Zammit-Mangion [email protected]
説明: 大規模なデータセットを使用した空間/時空間モデリングと予測のためのツール。このアプローチでは、一連の基底関数を使用して場、つまり共分散関数をモデル化します。この固定ランクの基底関数表現により、ビッグ データのモデリングが容易になり、この方法では当然、非定常の異方性共分散関数が可能になります。空間ドメインをいわゆる基本面積単位 (BAU) に離散化すると、さまざまなサポート (つまり、点参照サポートと面サポートの両方、場合によっては同時に) を使用した観測と、任意のユーザー指定領域にわたる予測の使用が容易になります。 FRK 、2D 平面や 3D 球体を含むさまざまな多様体にわたる推論もサポートしており、比較的簡単にモデル化、適合、予測、プロットするためのヘルパー関数を提供します。バージョン 2.0.0 以降では、一般化線形混合モデル (GLMM) フレームワークを採用することにより、非ガウス データ (ポアソン、二項、負の二項、ガンマ、逆ガウスなど) のモデリングもサポートされています。 Zammit-Mangion と Cressie (2021) は、ガウス設定でのFRKについて説明し、その基底関数と BAU の使用法について詳しく説明しています。 (2024) 非ガウス設定でのFRKについて説明します。これらの論文を要約し、追加の例を提供する 2 つのビネットが利用可能です。
ライセンス: GPL (>= 2)
library( " FRK " )
library( " sp " )
library( " ggplot2 " )
library( " ggpubr " )
# # Setup
m <- 1000 # Sample size
RNGversion( " 3.6.0 " ); set.seed( 1 ) # Fix seed
zdf <- data.frame ( x = runif( m ), y = runif( m )) # Generate random locs
zdf $ z <- sin( 8 * zdf $ x ) + cos( 8 * zdf $ y ) + 0.5 * rnorm( m ) # Simulate data
coordinates( zdf ) = ~ x + y # Turn into sp object
# # Run FRK
S <- FRK( f = z ~ 1 , # Formula to FRK
list ( zdf ), # All datasets are supplied in list
n_EM = 10 ) # Max number of EM iterations
pred <- predict( S ) # Prediction stage
# # Plotting
plotlist <- plot( S , pred )
ggarrange( plotlist = plotlist , nrow = 1 , legend = " top " )
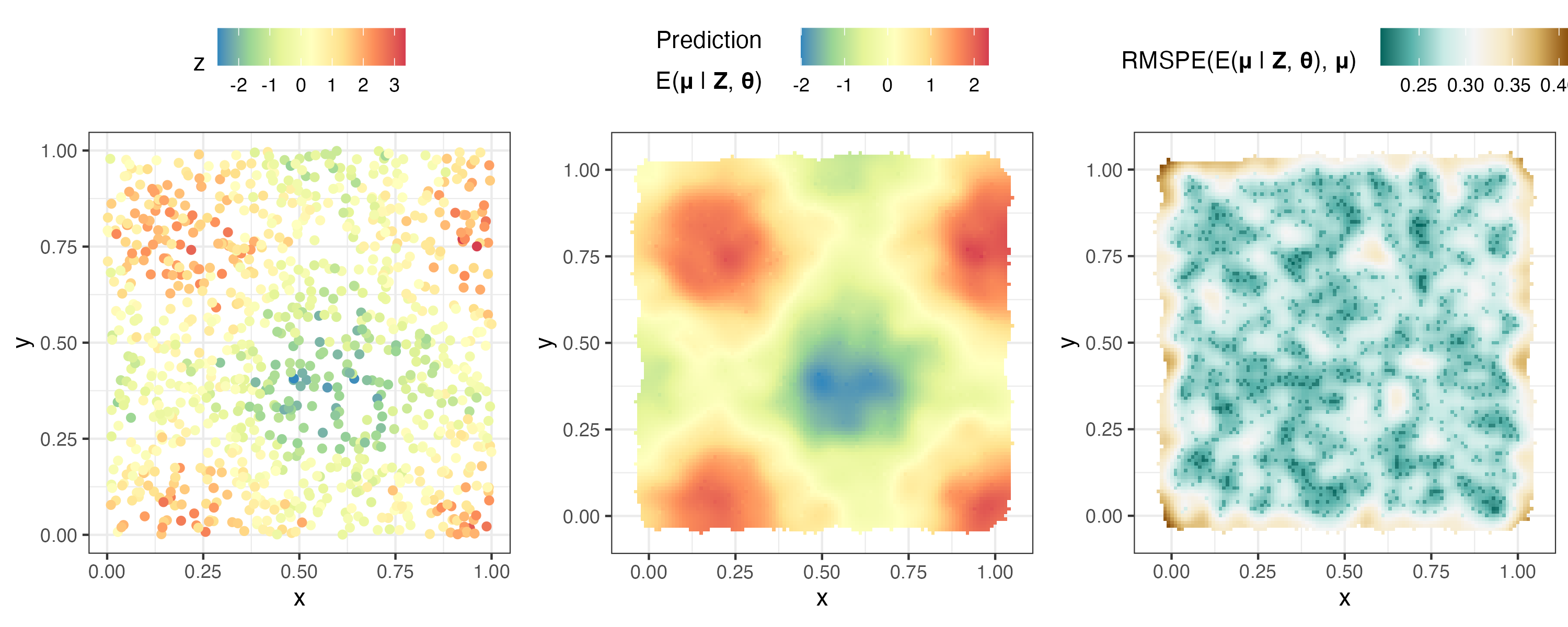
ここでは、シミュレートされたポアソン データを分析します。 FRK()でresponse = "poisson"およびlink = "sqrt"を設定することにより、平方根リンク関数を使用してモデル化された平均応答を持つポアソン データ モデルを表します。 FRKで使用できる他の非ガウス応答分布には、二項分布、負の二項分布、ガンマ分布、および逆ガウス分布があります。
# # Simulate Poisson data using the previous example's data to construct a mean
zdf $ z <- rpois( m , lambda = zdf $ z ^ 2 )
# # Run FRK
S <- FRK( f = z ~ 1 , list ( zdf ),
response = " poisson " , # Poisson data model
link = " sqrt " ) # square-root link function
pred <- predict( S )
# # Plotting
plotlist <- plot( S , pred $ newdata )
ggarrange( plotlist $ z , plotlist $ p_mu , plotlist $ interval90_mu ,
nrow = 1 , legend = " top " )
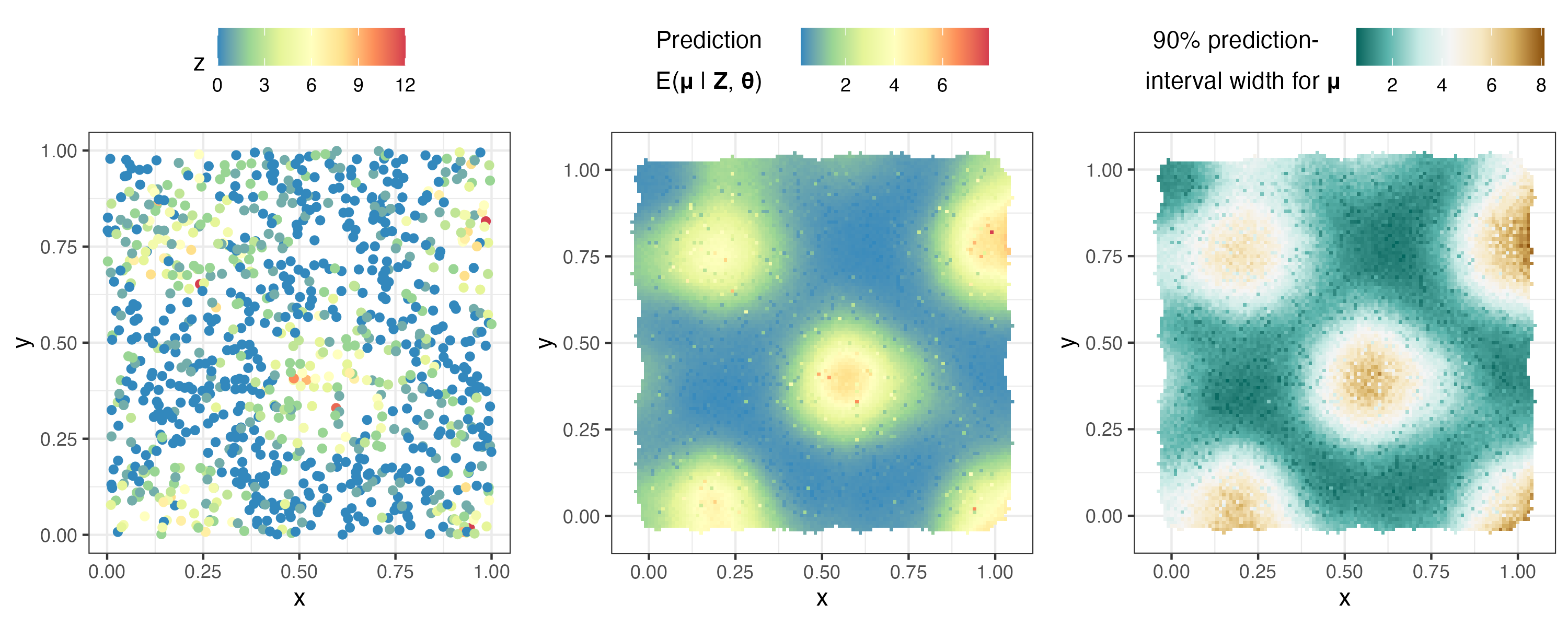
NOAA データセットを使用して、時空間データを分析します。
# # Setup
library( " spacetime " )
data( " NOAA_df_1990 " )
Tmax <- subset( NOAA_df_1990 , month %in% 7 & year == 1993 )
Tmax <- within( Tmax , { time = as.Date(paste( year , month , day , sep = " - " ))})
STObj <- stConstruct( x = Tmax , space = c( " lon " , " lat " ), time = " time " , interval = TRUE )
# # BAUs: spatial BAUs are 1x1 pixels, temporal BAUs are 1 day intervals
BAUs <- auto_BAUs( manifold = STplane(),
cellsize = c( 1 , 1 , 1 ),
data = STObj , tunit = " days " )
BAUs $ fs <- 1 # scalar fine-scale variance matrix, implicit in previous examples
# # Basis functions
G <- auto_basis( manifold = STplane(), data = STObj , nres = 2 , tunit = " days " )
# # Run FRK
STObj $ std <- 2 # fix the measurement error variance
S <- FRK( f = z ~ 1 + lat , data = list ( STObj ),
basis = G , BAUs = BAUs , est_error = FALSE , method = " TMB " )
pred <- predict( S , percentiles = NULL )
# # Plotting: include only some times via the argument subset_time
plotlist <- plot( S , pred $ newdata , subset_time = c( 1 , 7 , 13 , 19 , 25 , 31 ))
ggarrange( plotlist = plotlist , nrow = 1 , legend = " top " )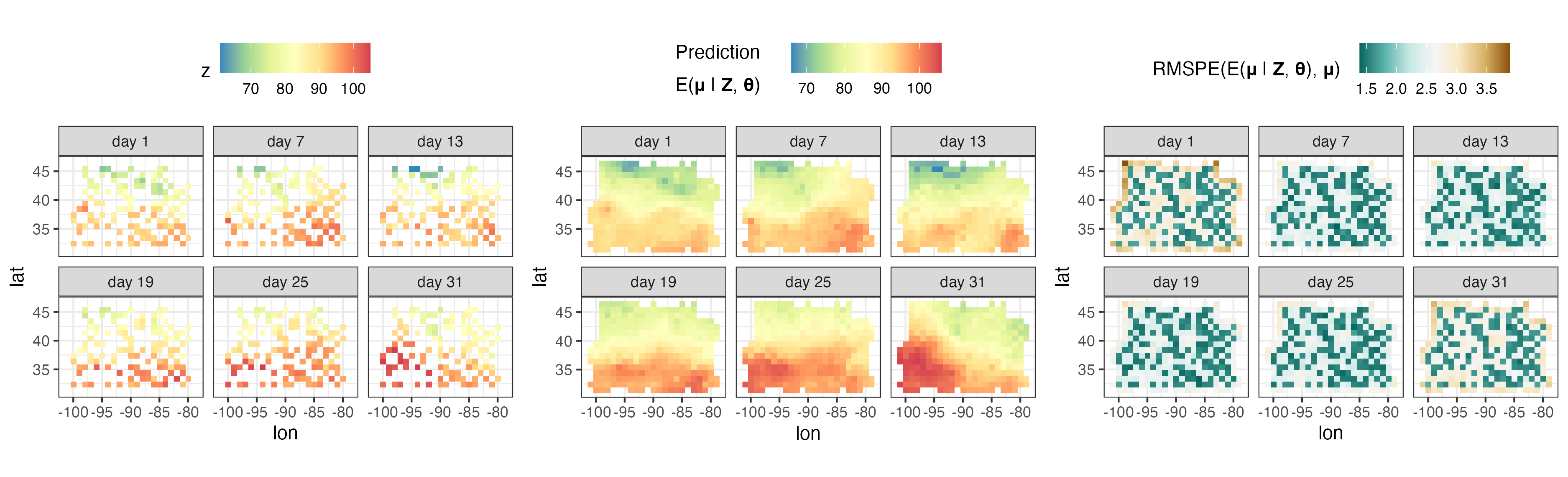
FRKパッケージは現在、衛星データによって観測されたフィールドの時空間アニメーションを生成するために使用されています。ここでは、2014 年 9 月から 2016 年 6 月までの NASA OCO-2 のデータを使用した CO2 の日次予測を示します。
FRK 六角ロゴをデザインしてくれた Michael Bertolacci に感謝します。