dsc 2 22 03 MLE gaussian lab bain trial jan19

正規分布を使用した MLE - ラボ

導入

このラボでは、前のレッスンで見た数式を実践して、MLE が正規分布でどのように機能するかを確認します。

目的

次のことができるようになります。

• MLE が正規分布でどのように機能するかを理解して説明する
• 正規分布を所定のデータに当てはめて平均と分散を特定します
• 近似分布と実際の分布を視覚的に比較する

注: *証明付きのすべての MLE 方程式の詳細な導出は、この Web サイトで参照できます。 *

Python の MLE

以下に Python を使用した MLE と分布フィッティングの例を見てみましょう。ここで、 scipy.stats.norm.fit最尤推定を使用して分布パラメーターを計算します。

必要なライブラリをインポートする

 from scipy . stats import norm # for generating sample data and fitting distributions
import matplotlib . pyplot as plt
plt . style . use ( 'seaborn' )
import numpy as np

平均 0 および標準偏差 1 の正規分布から 200 個のランダム サンプルの配列を生成します

 sample = None

MLE による分布フィッティング

- stats.norm.fit(data)を使用して、分布を上記のデータに適合させます。

- これは、MLE アプローチを介して 2 つのパラメーターのリストを返します: (mean,:parameters[0] および std:parameters[1])

 param = None

#param[0], param[1]
# (0.08241224761452863, 1.002987490235812)

a) 実際のデータパラメータ b) x = np.linspace(-5,5,100)を使用して近似されたパラメータから PDF を計算します。

 x = np . linspace ( - 5 , 5 , 100 )

# Generate the pdf from fitted parameters (fitted distribution)
fitted_pdf = None
# Generate the pdf without fitting (normal distribution non fitted)
normal_pdf = None

両方の PDF を視覚化する

 # Your code here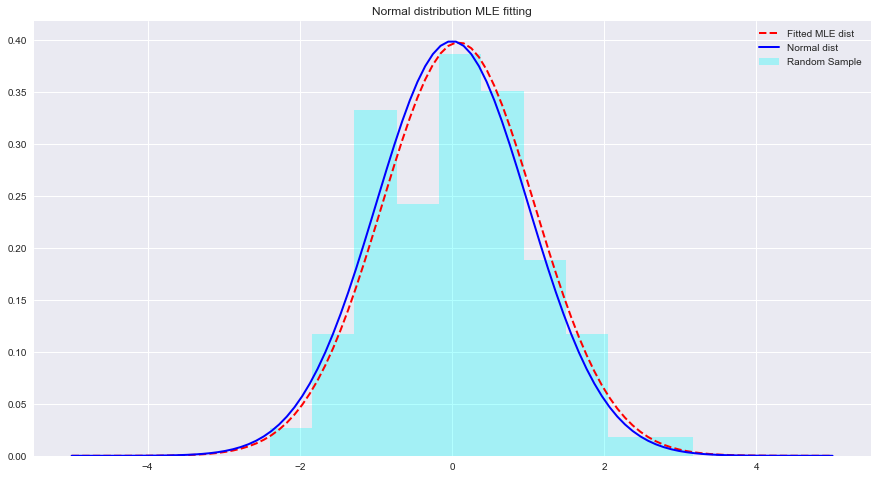 

 #  Your comments/observations 

まとめ

この短いラボでは、ガウスのコンテキスト、つまり基礎となる確率変数が正規分布している場合のベイジアン設定を調べました。 MLE は、期待される平均値の尤度を最大化することで、正規分布の未知のパラメーターを推定できることを学びました。期待される平均は、そのパラメーター空間内の非適合正規分布の平均に非常に近づきます。この理解を進めて、単純ベイズ分類器を使用してデータ分布に存在する多数のクラスの推定手段でそのような推定がどのように実行されるかを学習します。