非常に大きなキューブ用のルービックのキューブソルバー。
1〜65536の任意のサイズのキューブを解決します。コードを簡単に変更して、さらに大きなキューブを処理できます。ただし、主な制限は、システム上のメモリの量と解決にかかる時間です。解決時間の成長〜n^2は、各次元で2倍大きいキューブを解くのに4〜5倍時間がかかることを意味します。
1024階建てのキューブは、約1.5秒で解決できます。 16384階建てのキューブは、約20分で解決できます。
YouTube:65536レイヤーの解決YouTube:32768レイヤーを解く
32768キューブの前面の画像
センターを解き、次に角を曲がります
センターは、各ステージが特定の色のすべてのピースを1つの顔から希望の顔に移動する15段階で解決されます。例:ステージは、白い顔のすべての緑色の部分を緑色の顔に移動します。これをすべての色と顔に繰り返します。
ソルバーは、ここで説明する整流子を使用します。ここでは、顔のある象限から別の顔の象徴的な象限に中央の部分を通勤できます。この整理者の非常に重要な特性は、単一の列に多くのピースを同時に移動するように変更できることです。非常に大きなキューブの場合、これは、単一の操作で数千個ではないにしても数百個のピースを移動できることを意味します。動きの平均数k =(2 * p + 5) / pここで、pは操作ごとに移動できる部分の数です。 Kは、キューブのサイズが大きくなるとすぐに2に近づきます。
コーナーは、角を所定の位置に移動し、顔が正しく向き付けるまで回転する基本的なブルートフォース方法を使用して解決されます。ウィル・スミスは説明できます:https://www.youtube.com/watch?v=wbzkdrc9vqs
エッジは、すべてのエッジを前面に移動することで解決され、左端から右端に目的のピースを交換します。パリティの問題を修正または防止するために必要な多くの機能。
顔の回転は本質的に無料です。特定の顔(n^2ピース)にすべてのピースを移動して回転を実行する代わりに、ソルバーは、顔に読み取り/書き込みに使用する座標系を単純に変更します。これにより、膨大な量のデータ交換が節約されます。
// Virtually rotate this face by q * 90 degrees
inline void Face::RotatefaceCW ( const int q)
{
orientation = (orientation + q) & 3 ;
}
// Gets the value of this face at coordinates r = row, c = column
inline const byte Face::GetRC ( const uint r, const uint c) const
{
switch (orientation) {
case 0 :
return data[(r << BS) + c];
case 1 :
return data[(c << BS) + (R1 - r)];
case 2 :
return data[((R1 - r) << BS) + (R1 - c)];
case 3 :
return data[((R1 - c) << BS) + r];
default :
return 0 ;
}
}このコードには、使用される単純な画像輸出業者が含まれており、各面を画像にします。
https://www.nayuki.io/page/tiny-png output
https://github.com/nayuki/nayuki-web-published-code
Tiny PNG出力は、CおよびC ++で利用できる小さなスタンドアロンライブラリで、RGB8.8.8ピクセルを使用してPNGファイルを書き込みます。
移動の総数は、単純な式を使用して推定できます。キューブが十分にランダム化されていると仮定すると、最初の顔が1/6の解決されると予想されるため、5/6のピースを移動する必要があります。 2番目の顔は1/5が解決され、4/5のピースを移動する必要があります。 3番目の顔3/4、4番目の顔2/3、5番目の顔1/2、最後の顔は完全に解決されます。シングルピースを移動するための動きの平均数(k)は、実験的に〜2.1と推定できます。キューブのサイズが大きくなると、Kの値が減少します。整流子は少なくとも2回移動する必要があるため、値は2未満になることはありません。
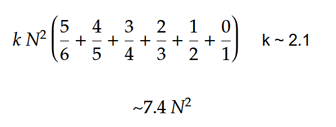
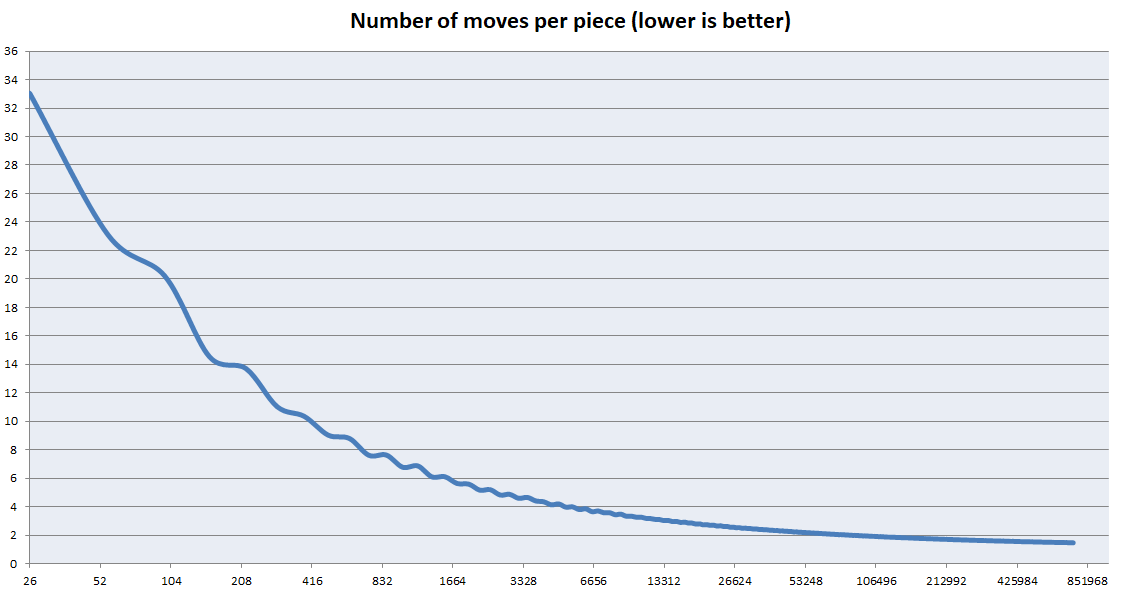
このアルゴリズムは、非常に大きなキューブ用に最適化されています。しかし、小さな立方体にとってはひどいです。主な最適化は、センターをできるだけ早く解決することに焦点を当てており、エッジの解決については考慮されませんでした。ただし、エッジのサイズは、キューブのサイズが増加するにつれて、中心と比較して取るに足らないものです。以下のグラフは、ピースあたりの移動の平均数が大きい立方体でどのように減少するかを示しています。注:これはkのグラフではありません。それは(合計ムーブ) /(ピース数)のグラフです
cmake -B build -S .
cd build
cmake --build .
RCube/RCube