Tesla Stock Price Prediction

시계열 분석

• 시계열 모델을 통한 Tesla 주식 예측 Yahoo Finance를 통해 Tesla Company의 주식 정보(NASDAQ: TSLA)를 얻습니다. 이 프로젝트에서는 시계열 분석 방법을 적용하여 TSLA의 기본 정보를 조사하고 TLSA의 시계열을 분해합니다.
• 향후 365일 동안 TSLA의 가격을 예측하는 지수 평활 방법은 다음과 같습니다.
• 가격을 예측하는 ARIMA 모델. 이 프로젝트에서는 또한 모델의 성능을 확인하기 위해 오류 분포를 예측합니다.

시계열 분해

시계열을 분해한다는 것은 시계열을 구성 성분(보통 추세 성분과 불규칙 성분)으로 분리하고, 계절 시계열인 경우 계절 성분으로 분리하는 것을 의미합니다. TSLA 주식 정보의 경우 가격 추세 그래프를 보면 데이터 내에 계절적 요소가 없음을 알 수 있습니다. 하지만 이 시계열 데이터에는 추세 구성요소와 불규칙 구성요소가 포함되어야 합니다. 시계열을 분해하는 것은 시계열을 이러한 구성요소로 분리하는 것, 즉 추세 구성요소와 불규칙 구성요소를 추정하는 것을 포함합니다. TSLA 데이터를 평활화하기 위해 SMA() 함수를 사용하겠습니다. 추세 구성요소를 확인하기 위해 다른 차수(n=8 및 n=40)를 선택하겠습니다. 목표는 간단한 이동 평균을 사용하여 데이터를 평활화하는 것입니다.

예측 모델 및 평가: 지수평활

• 지수 평활 모델
  지수평활 모델은 시계열 데이터에 대한 단기 예측을 만드는 데 사용될 수 있습니다. TSLA 데이터를 통해 우리는 이것이 계절성이 없는 가법 모델로 설명될 수 있음을 알고 있습니다. 추세 차트에서 시계열의 무작위 변동은 시간이 지남에 따라 크기가 거의 일정한 것처럼 보입니다. 따라서 우리는 간단한 지수평활 예측을 맞추기 위해 HoltWinter() 함수를 사용할 것입니다.

예측 모델 및 평가: ARIMA 모델

ARIMA 모델

ARIMA(Autoregressive Integrated Moving Average)는 시계열 분석에서 현재 값을 기반으로 변수의 미래 값을 예측하는 데 사용되는 주요 도구입니다. ARIMA(p,d,q) 예측 방정식: ARIMA 모델은 이론적으로 차분을 통해 "정상"으로 만들 수 있는 시계열을 예측하기 위한 가장 일반적인 클래스의 모델입니다. ARIMA 모델은 고정 시계열에 대해 정의됩니다. 따라서 비정상 시계열로 시작하는 경우 먼저 고정 시계열을 얻을 때까지 시계열을 '차이'해야 합니다. 고정된 시계열을 얻기 위해 시계열의 d배 차이를 얻으려면 diff() 함수를 사용합니다. 그런 다음 A 형식 ADF 테스트를 사용하여 비정상성의 귀무 가설을 기각하지 않고 육안 검사를 확인합니다.

요약

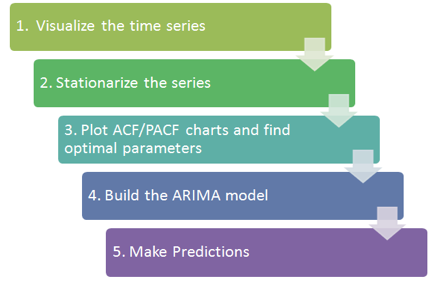
이 섹션에서는 TESLA 주식 데이터를 시계열로 사용합니다. 이를 분해하고 HoltWinter 지수평활과 ARIMA를 사용하여 미래 주가를 예측합니다. 기본적인 절차는 다음 그림과 같습니다.

또 다른 점은 더 나은 결과를 얻기 위해 항상 오류를 분석하고 모델 매개변수를 조정해야 한다는 것입니다.