
이것은 DSA.js 책의 코딩 구현과 NPM 패키지의 저장소입니다.
이 저장소에서는 JavaScript의 알고리즘 및 데이터 구조 구현을 찾을 수 있습니다. 이 자료는 개발자를 위한 참조 매뉴얼로 사용하거나 인터뷰 전에 특정 주제를 새로 고칠 수 있습니다. 또한 문제를 보다 효율적으로 해결하기 위한 아이디어를 찾을 수도 있습니다.
저장소를 복제하거나 NPM에서 코드를 설치할 수 있습니다.
npm install dsa.js그런 다음 이를 프로그램이나 CLI로 가져올 수 있습니다.
const { LinkedList , Queue , Stack } = require ( 'dsa.js' ) ;사용 가능한 모든 데이터 구조 및 알고리즘 목록은 index.js를 참조하세요.
알고리즘은 모든 프로그래머에게 필수적인 도구 상자입니다.
데이터를 정렬하고, 대규모 데이터 세트에서 값을 검색하고, 데이터를 변환하고, 코드를 여러 사용자에 맞게 확장해야 하는 경우 알고리즘 런타임을 염두에 두어야 합니다. 알고리즘은 문제를 해결하기 위해 따르는 단계인 반면, 데이터 구조는 나중에 조작할 수 있도록 데이터를 저장하는 곳입니다. 둘 다 결합하여 프로그램을 만듭니다.
알고리즘 + 데이터 구조 = 프로그램.
대부분의 프로그래밍 언어와 라이브러리는 실제로 기본 데이터 구조와 알고리즘에 대한 구현을 제공합니다. 그러나 데이터 구조를 적절하게 사용하려면 작업에 가장 적합한 도구를 선택하기 위한 장단점을 알아야 합니다.
이 자료에서는 다음을 가르칩니다.
모든 코드와 설명은 이 저장소에서 확인할 수 있습니다. (src 폴더)에서 링크와 코드 예제를 살펴볼 수 있습니다. 그러나 인라인 코드 예제는 (Github의 asciidoc 제한으로 인해) 확장되지 않지만 경로를 따라 구현을 볼 수 있습니다.
참고: 정보를 보다 선형적으로 활용하고 싶다면 책 형식이 더 적합할 것입니다.
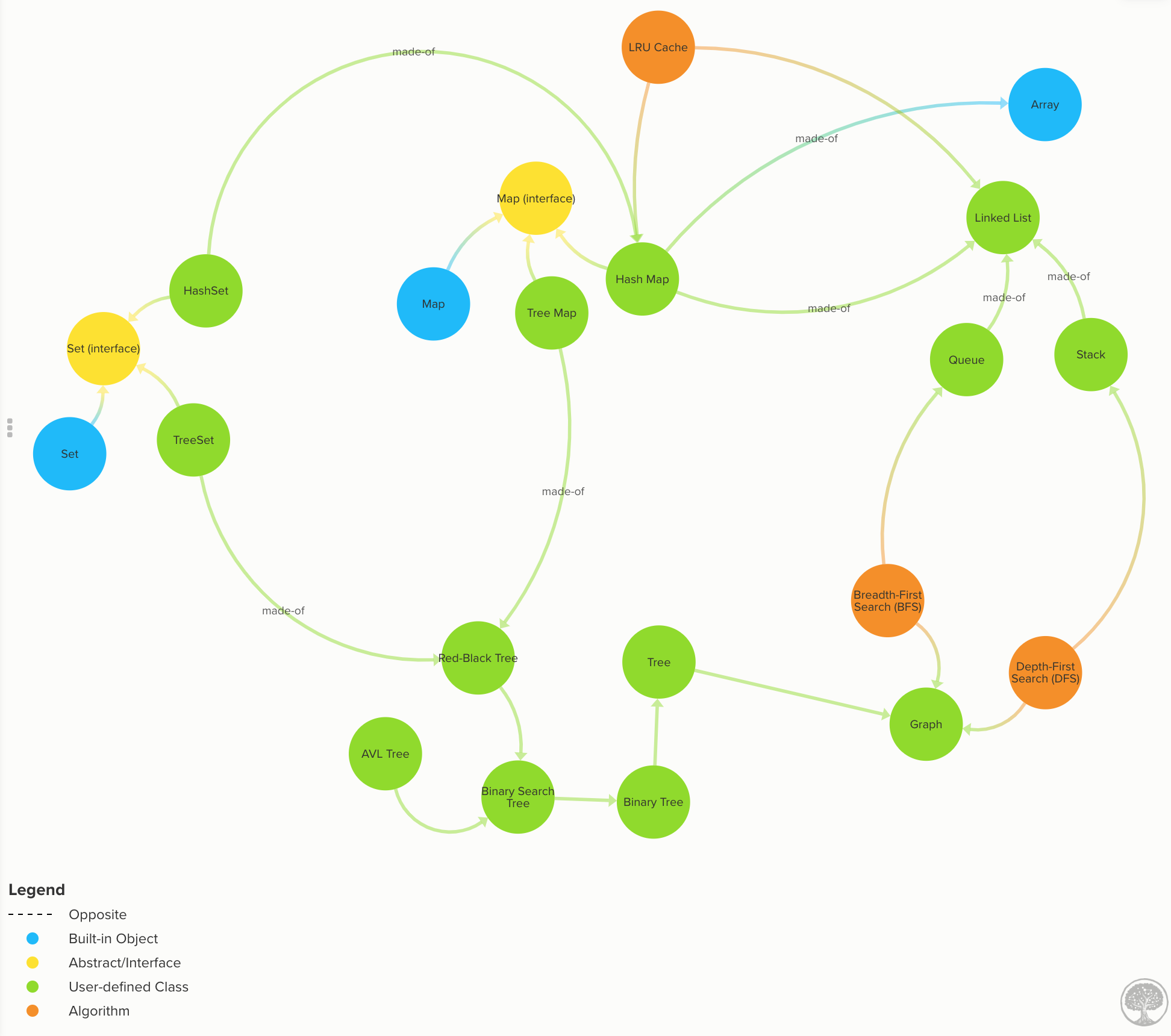
주제는 아래에서 볼 수 있듯이 네 가지 주요 범주로 나뉩니다.
컴퓨터 공학은 말도 안 되는 내용 없이도 문제가 됩니다. (확대하려면 클릭하세요)
모든 허황된 내용 없이 컴퓨터 과학 덩어리
코드 예제를 통해 런타임 계산 방법 알아보기
Big O 표기법을 사용하여 알고리즘을 비교하는 방법을 알아보세요. (확대하려면 클릭하세요)
Big O 표기법을 사용하여 알고리즘을 비교하는 방법을 알아보세요.
Big O 표기법을 사용한 알고리즘 비교
배열에서 중복 항목을 찾고 싶다고 가정해 보겠습니다. Big O 표기법을 사용하면 동일한 문제를 해결하는 다양한 솔루션을 비교할 수 있지만 이를 수행하는 데 걸리는 시간은 엄청나게 다릅니다.
- 지도를 활용한 최적의 솔루션
- 배열에서 중복 찾기(순진한 접근 방식)
시간 복잡도를 계산하는 방법을 코드와 함께 설명하는 8가지 예. (확대하려면 클릭하세요)
시간 복잡도를 계산하는 방법을 코드로 설명하는 8가지 예
가장 일반적인 시간 복잡성
시간 복잡도 그래프
가장 일반적인 데이터 구조의 모든 것을 이해합니다. (확대하려면 클릭하세요)
가장 일반적인 데이터 구조의 모든 것을 이해합니다.
배열: 대부분의 언어에 내장되어 있으므로 여기서는 구현되지 않습니다. 배열 시간 복잡도
연결 목록: 각 데이터 노드에는 다음(및 이전)에 대한 링크가 있습니다. 코드 | 연결 목록 시간 복잡도
대기열: 데이터는 "선입선출(FIFO)" 방식으로 흐릅니다. 코드 | 대기열 시간 복잡성
스택: 데이터는 "LIFO(후입선출)" 방식으로 흐릅니다. 코드 | 스택 시간 복잡성
배열 또는 연결 목록을 사용하는 경우 장단점을 알아보세요. (확대하려면 클릭하세요)
배열 또는 연결 목록을 사용하는 경우 장단점을 알아라
다음과 같은 경우에 배열을 사용하세요.
- (인덱스를 사용하여) 무작위 순서로 빠르게 데이터에 액세스해야 합니다.
- 데이터는 다차원적입니다(예: 행렬, 텐서).
다음과 같은 경우에 연결 목록을 사용하십시오.
- 귀하는 귀하의 데이터에 순차적으로 접근하게 됩니다.
- 메모리를 절약하고 필요할 때만 메모리를 할당하려고 합니다.
- 목록의 극단에서 제거/추가하는 데 일정한 시간이 필요합니다.
- 크기 요구 사항을 알 수 없는 경우 - 동적 크기 이점
목록, 스택 및 대기열을 구축합니다. (확대하려면 클릭하세요)
처음부터 목록, 스택 및 대기열 구축
다음 데이터 구조를 처음부터 구축하세요.
- 연결리스트
- 스택
- 대기줄
가장 다양한 데이터 구조 중 하나인 해시 맵을 이해하세요. (확대하려면 클릭하세요)
해시맵
다음과 같은 다양한 유형의 지도를 구현하는 방법을 알아보세요.
- 해시맵
- 트리맵
또한 다양한 지도 구현 간의 차이점을 알아보세요.
HashMap시간 효율적입니다.TreeMap공간 효율적입니다.TreeMap검색 복잡도는 O(log n) 인 반면, 최적화된HashMap은 평균 O(1) 입니다.HashMap의 키는 삽입 순서(또는 구현에 따라 무작위)입니다.TreeMap의 키는 항상 정렬됩니다.TreeMap최소값 얻기, 최대값 얻기, 중앙값 얻기, 키 범위 찾기와 같은 일부 통계 데이터를 무료로 제공합니다.HashMap그렇지 않습니다.TreeMap항상 O(log n) 을 보장하는 반면,HashMap의 상각 시간은 O(1) 이지만 드물게 재해시하는 경우에는 O(n) 이 필요합니다.그래프와 트리의 속성을 알아보세요. (확대하려면 클릭하세요)
그래프와 트리의 속성을 알아보세요
그래프
많은 이미지와 일러스트레이션을 통해 그래프의 모든 속성을 알아보세요.
그래프 : 0개 이상의 인접 노드에 대한 연결 또는 가장자리를 가질 수 있는 데이터 노드입니다 . 트리와 달리 노드에는 여러 부모, 루프가 있을 수 있습니다. 코드 | 그래프 시간 복잡도
나무
다양한 종류의 나무와 그 특성을 알아보세요.
트리 : 데이터 노드에는 하위 노드라고도 불리는 0개 이상의 인접 노드가 있습니다. 각 노드는 하나의 상위 노드만 가질 수 있습니다. 그렇지 않으면 트리가 아닌 그래프입니다. 코드 | 문서
이진 트리(Binary Trees) : 트리와 동일하지만 최대 2개의 자식만 가질 수 있습니다. 코드 | 문서
이진 검색 트리 (BST): 이진 트리와 동일하지만 노드 값은
left < parent < right순서를 유지합니다. 코드 | BST 시간 복잡도AVL 트리 : 조회 시간을 최대화하기 위한 자체 균형 BST입니다. 코드 | AVL 트리 문서 | 자체 균형 조정 및 트리 회전 문서
Red-Black Trees : 삽입 속도를 최대화하기 위해 AVL보다 느슨한 자체 균형 BST. 암호
빠른 조회를 위해 이진 검색 트리를 구현합니다.
빠른 조회를 위한 이진 검색 트리 구현
트리에서 값을 추가/제거/업데이트하는 방법을 알아보세요.
나무의 균형을 맞추는 방법은 무엇입니까?
불균형 BST에서 균형 BST로
1 2 / 2 => 1 3 3
7가지 간단한 단계로 문제를 해결하는 데 어려움을 겪지 마세요. (확대하려면 클릭하세요)
8가지 간단한 단계로 문제를 해결하는 데 어려움을 겪지 마세요.
- 문제를 이해하다
- 간단한 예제 작성(아직 엣지 케이스 없음)
- 브레인스토밍 솔루션(탐욕 알고리즘, 분할 및 정복, 역추적, 무차별 대입)
- 간단한 예를 통해 답을 테스트해보세요(정신적으로)
- 솔루션 최적화
- 코드를 작성하세요. 네, 이제 코딩을 할 수 있습니다.
- 작성된 코드를 테스트하세요
- 공간과 시간 모두의 복잡성을 분석하고 추가로 최적화하세요.
자세한 내용은 여기
가장 널리 사용되는 정렬 알고리즘(병합 정렬, 퀵 정렬 등)을 마스터하세요. (확대하려면 클릭하세요.)
가장 인기 있는 정렬 알고리즘을 마스터하세요
오버헤드가 낮은 세 가지 필수 정렬 알고리즘 O(n^2)을 살펴보겠습니다.
버블 정렬. 코드 | 문서
삽입 정렬. 코드 | 문서
선택 정렬. 코드 | 문서
그런 다음 다음과 같은 효율적인 정렬 알고리즘 O(n log n)에 대해 논의합니다.
병합 정렬. 코드 | 문서
퀵소트. 코드 | 문서
분할 정복, 동적 프로그래밍, 그리디 알고리즘, 역추적과 같은 문제를 해결하기 위한 다양한 접근 방식을 알아보세요. (확대하려면 클릭하세요)
알고리즘 문제를 해결하기 위한 다양한 접근 방식을 알아보세요.
우리는 알고리즘 문제를 해결하기 위한 다음 기술에 대해 논의할 것입니다.
- 탐욕 알고리즘(Greedy Algorithms): 뒤돌아보지 않고 최상의 솔루션을 찾기 위해 휴리스틱을 사용하여 탐욕스러운 선택을 합니다.
- 동적 프로그래밍: 겹치는 하위 문제가 많을 때 재귀 알고리즘의 속도를 높이는 기술입니다. 작업이 중복되는 것을 방지하기 위해 메모이제이션을 사용합니다.
- 분할 및 정복: 문제를 더 작은 조각으로 나누고 각 하위 문제를 정복한 다음 결과를 합칩니다 .
- 역추적: 가능한 모든 경로(또는 일부) 를 검색합니다. 그러나 현재 솔루션이 작동하지 않는 것을 확인하는 즉시 중지하고 다시 돌아갑니다 .
- 무차별 대입(Brute Force) : 가능한 모든 솔루션을 생성하고 모두 시도합니다. (최후의 수단이나 출발점으로 사용하십시오).
프로그래머로서 우리는 매일 문제를 해결해야 합니다. 문제를 잘 해결하고 싶다면 다양한 솔루션에 대해 알아두는 것이 좋습니다. 종종 스스로 답을 찾는 것보다 기존 리소스를 배우는 것이 더 효율적입니다. 도구와 연습이 많을수록 좋습니다. 이 책은 데이터 구조 간의 장단점과 알고리즘 성능에 대한 이유를 이해하는 데 도움이 됩니다.
자바스크립트 알고리즘에 관한 책은 많지 않습니다. 이 자료는 공백을 메웁니다. 또한, 좋은 습관입니다 :)
예, [Slack 채널](https://dsajs-slackin.herokuapp.com)에서 이슈를 열거나 질문하세요.
이 프로젝트는 책으로도 볼 수 있습니다. 180페이지 이상 + ePub 및 Mobi 버전으로 구성된 멋진 형식의 PDF를 받게 됩니다.
다음 중 한 곳으로 연락주세요!
@iAmAdrianMejiadsajs.slack.com 에서 채팅