smard power forecasting
1.0.0
이 저장소는 독일의 전력 소비를 예측하기 위한 것입니다.
다음을 기반으로 하고 영감을 받았습니다.
데이터 소스: SMARD
다운로드한 모든 파일을 다음 위치에 넣으세요.
/example/dataset # there is already used dataset included if you pull, but you could update
Forecast.Rmd 파일을 확인하여 업데이트된 SMARD-Data 버전에서 이 코드를 실행할 수 있는 방법을 알아보세요.
사용된 라이브러리:
# Probably needed
# Load Packages
# library(fhswf)
# library(tsibbledata)
# library(broom)
# library(readr)
# library(datasets)
# library(timeDate)
# library(qlcal)
# library(corrplot)
# library(mgcv)
# library(MEFM)
# library(TTR)
packages <- c(
"devtools",
"ggplot2",
"dplyr",
"tsibble",
"fable",
"fabletools",
"feasts",
"distributional",
"lubridate",
"tidyr",
"forecast",
"zoo",
"scales",
"fable.prophet"
)
install.packages(packages)
library(devtools)
library(ggplot2)
library(dplyr)
library(tsibble)
library(fable)
library(fabletools)
library(feasts)
library(distributional)
library(lubridate)
library(tidyr)
library(forecast)
library(zoo)
library(scales)
library(fable.prophet)
시작하려면 example/ 폴더에서 작업해 보세요.
# Define datapaths
power_consum_path <- "dataset\stunde_2015_2024\Realisierter_Stromverbrauch_201501010000_202407090000_Stunde.csv"
power_consum_smard_prediction_path <- "dataset\propgnose_vom_smard\Prognostizierter_Stromverbrauch_202401010000_202407090000_Stunde.csv"
# Load Smard Prediction
power_consum_smard_prediction_loaded <- load_power_consum(path=power_consum_smard_prediction_path)
raw_smard_pred <- power_consum_smard_prediction_loaded$raw_data
cleaned_smard_pred <- power_consum_smard_prediction_loaded$cleaned_data
cleaned_smard_pred <- cleaned_smard_pred |>
mutate(.model = "SMARD")
names(cleaned_smard_pred)[names(cleaned_smard_pred) == "PowerConsum"] <- ".mean"
# Load PowerConsum Data
power_consum_loaded <- load_power_consum(path=power_consum_path)
raw_power_consum <- power_consum_loaded$raw_data
cleaned_power_consum <- power_consum_loaded$cleaned_data
# Generate more features
cleaned_power_consum$localName[is.na(cleaned_power_consum$localName)] = "Working-Day"
cleaned_power_consum$MeanLastWeek <- rollapply(cleaned_power_consum$PowerConsum, width = 24*8, FUN = function(x) mean(x[1:(24*8-25)]), align = "right", fill = NA)
cleaned_power_consum$MeanLastTwoDays <- rollapply(cleaned_power_consum$PowerConsum, width = 24*3, FUN = function(x) mean(x[1:(24*3-25)]), align = "right", fill = NA)
cleaned_power_consum$MaxLastOneDay <- rollapply(cleaned_power_consum$PowerConsum, width = 24*2, FUN = function(x) max(x[1:(24*2-25)]), align = "right", fill = NA)
cleaned_power_consum$MinLastOneDay <- rollapply(cleaned_power_consum$PowerConsum, width = 24*2, FUN = function(x) min(x[1:(24*2-25)]), align = "right", fill = NA)
데이터세트와 Holiday API에서 다음 기능이 생성되었습니다.
| 색인 | 열 이름 | 설명 |
|---|---|---|
| 1 | 날짜시작 | DateIndex 검증용(비슷하지만 원시) |
| 2 | 전력 소비 | 전력 소비량(MW) |
| 3 | 날짜 인덱스 | 타임스탬프(yyyy-mm-dd hh:mm:ss) |
| 4 | 주일 | Mo, Di, Mi, Do, Fr, Sa, So(독일어로 된 평일) |
| 5 | 날짜 | 날짜(yyyy-mm-dd) |
| 6 | 년도 | 년도 |
| 7 | 주 | 주 번호 0-53 |
| 8 | 시간 | 시간 번호 0-24 |
| 9 | 월 | 월 번호 1-12 |
| 10 | 지역 이름 | 타임스탬프의 휴일 이름 |
| 11 | 근무일 | 1/0 Workday(Werktag)인 경우 1 |
| 12 | 모 | 1/0 월요일이면 1 |
| 13 | 디 | 1/0 화요일이면 1 |
| 14 | 미 | 1/0 수요일이면 1 |
| 15 | 하다 | 1/0 목요일이면 1 |
| 16 | 정말로 | 1/0 금요일이면 1 |
| 17 | 사 | 1/0 토요일이면 1 |
| 18 | 그래서 | 1/0 일요일이면 1(월-토요일을 사용하는 경우 필요하지 않음) |
| 19 | 휴일 | 1/0 공휴일이면 1 |
| 20 | 근무일휴일주말 | 휴일, 주말 또는 근무일인 경우(플롯의 경우 Char입니다.) |
| 21 | 휴일과일일 | 1/0 공휴일이 평일이면 1 |
| 22 | 마지막 날은 일하지 않은 날이었습니다. | 1/0 마지막 날이 근무일이 아닌 경우 1 |
| 23 | 지난 날은 일하지 않은 날이었고지금은 일하는 날 | 1/0 마지막 날이 근무일이 아니고 지금이 근무일인 경우 1 |
| 24 | 다음일은일하지않는일그리고지금일하는일 | 1/0 다음 날이 근무일이 아니고 지금은 근무일인 경우 1 |
| 25 | 지난 날은 휴일이었고 주말은 아니었습니다. | 1/0 마지막 날이 공휴일이고 주말이 아닌 경우 1 |
| 26 | 다음날은휴일이고주말이아닙니다 | 1/0 다음날이 공휴일이고 주말이 아닌 경우 1 |
| 27 | 휴일 이름 | localName(휴일 이름)과 유사 |
| 28 | 연말 | 1/0 연말인 경우(52주차 또는 53주차) |
| 29 | 올해의 첫 번째 주 | 1/0 연초(1주차)인 경우 |
| 30 | 휴일연장 | 1/0 연휴(다음날부터 6시간) |
| 31 | 휴일 스무딩 | HolidayExtend + sin(2*pi(시간)+1)/24) |
| 32 | 지난 주 평균 | 지난주 평균 소비전력(교대근무: 24*8-25) |
| 33 | 평균 지난 2일 | 지난 2일 동안의 평균 전력 소비량(교대: 24*3-25) |
| 34 | 최대지난1일 | 마지막 날 최대 소비 전력 (교대: 24*2-25) |
| 35 | 최소최근1일 | 마지막 날의 최소 전력 소비량 (교대: 24*2-25) |
이 연구에는 2015년부터 2024년까지 SMARD의 독일 전력 소비에 대한 데이터 세트가 있습니다.
그림 1은 누락된 값(빨간색), 중복된 타임스탬프(어두운색) 및 시간 경과에 따른 전력 소비(회색), 시간별 해상도가 있는 원시 데이터세트를 보여줍니다. 누락된 값이 하나 있고 매년 중복되는 값이 하나 있으므로 데이터세트를 정리하기가 쉬웠습니다. 전체적으로 거의 깨끗한 세트입니다. 데이터 세트를 정리한 후 전력 소비에 대한 그럴듯한 관찰이 있습니다.
마지막 관찰을 통해 간격을 메우는 간단한 접근 방식이 있습니다(해상도가 충분히 크고 결측값이 거의 없기 때문에 가능함). 중복을 위해 첫 번째 값이 유지되었습니다.
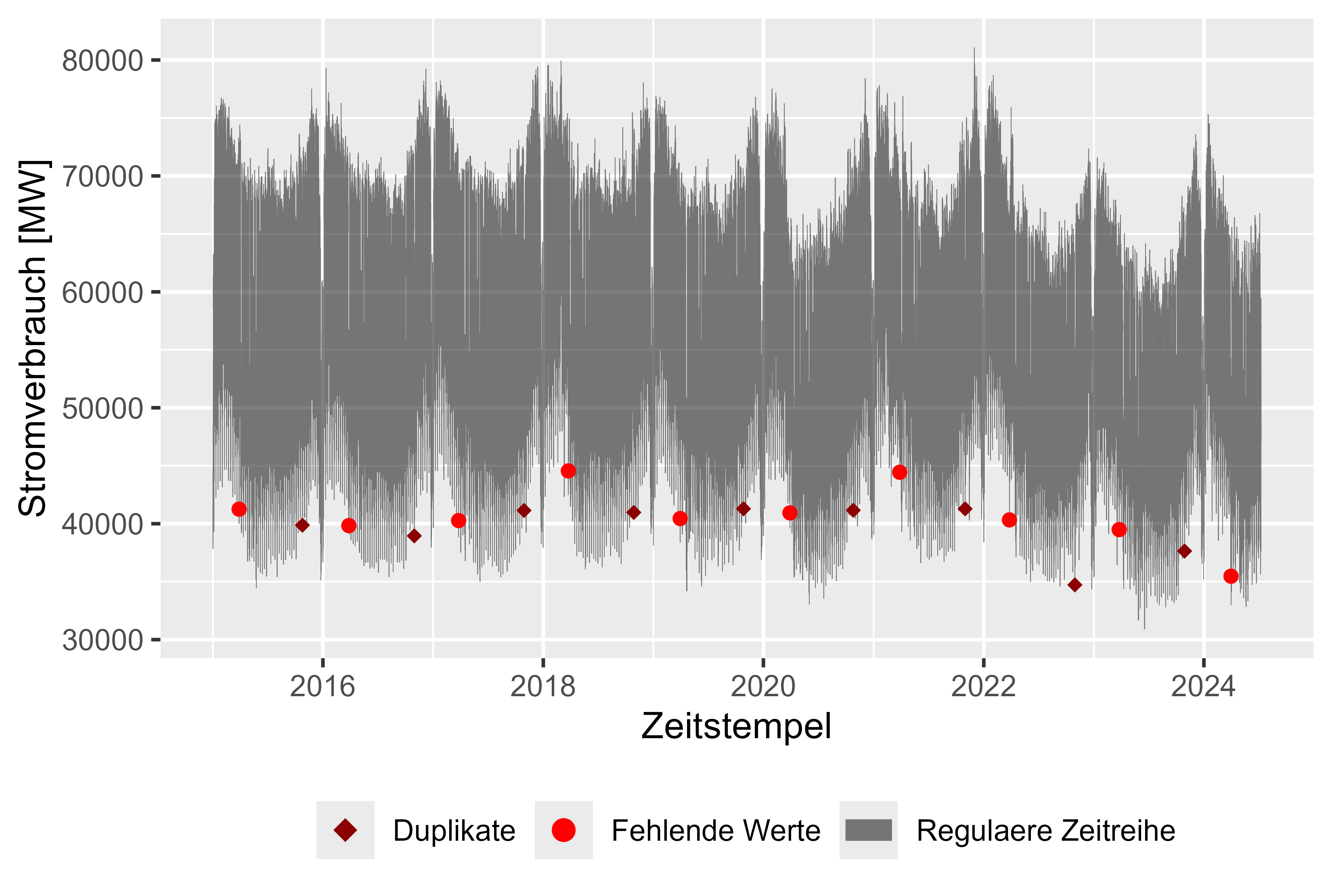그림 1 원시 전력 소비
local_name_colors <- c(
"Christi Himmelfahrt" = palette()[2],
"Erster Weihnachtstag" = palette()[2],
"Karfreitag" = palette()[2],
"Neujahr" = palette()[2],
"Ostermontag" = palette()[2],
"Pfingstmontag" = palette()[2],
"Reformationstag" = palette()[2],
"Tag der Arbeit" = palette()[2],
"Tag der Deutschen Einheit" = palette()[2],
"Zweiter Weihnachtstag" = palette()[2],
"Regulärer Tag" = palette()[1]
)
week_colors <- c(
"Mo" = palette()[1],
"Di" = palette()[1],
"Mi" = palette()[1],
"Do" = palette()[1],
"Fr" = palette()[1],
"Sa" = palette()[2],
"So" = palette()[2]
)
working_colors <- c("1" = "#2E9FDF", "0" = "#FC4E07")
whw_colors <- c(
"FeiertagnKein Wochenende" = "black",
"Kein FeiertagnKein Wochenende" = "red",
"Kein FeiertagnWochenende" = "orange",
"FeiertagnWochenende" = "blue"
)
p <- cleaned_power_consum |>
gg_tsdisplay(PowerConsum, plot_type = "partial", lag = 100)
ggsave(
"plots/power_consum_acf_pacf.png",
plot = p,
width = 5.5,
height = 3.7,
dpi = 600
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MinLastOneDay.png",
x = "MinLastOneDay",
y = "PowerConsum",
x_label = "Minimaler Stromverbrauch vom letzten Tag [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MaxLastOneDay.png",
x = "MaxLastOneDay",
y = "PowerConsum",
x_label = "Maximaler Stromverbrauch vom letzten Tag [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MeanLastWeek.png",
x = "MeanLastWeek",
y = "PowerConsum",
x_label = "Durchschnittlicher Stromverbrauch der letzten 7 Tage [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MeanLastTwoDays.png",
x = "MeanLastTwoDays",
y = "PowerConsum",
x_label = "Durchschnittlicher Stromverbrauch der letzten 2 Tage [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "WorkdayHolidayWeekend",
file_name = "plots\workday_holiday_weekend_histogram.png",
colors = whw_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Wochenende oder Feiertage",
name_1 = "Werktag"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "WorkDay",
file_name = "plots\workday_histogram.png",
colors = working_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Wochenende oder Feiertage",
name_1 = "Werktag"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "Holiday",
file_name = "plots\holiday_histogram.png",
colors = working_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Werktag oder Wochenende",
name_1 = "Feiertag"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "HolidayAndWorkDay",
file_name = "plots\holiday_workday_histogram.png",
colors = working_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Wochenende oder Werktag",
name_1 = "Feiertag am Werktag"
)
plot_by_group(
cleaned_power_consum,
group_name = "HolidayName",
file_name = "plots\holiday_boxplot.png",
colors = local_name_colors,
title = "Übersicht der einzelnen Feiertage",
y="PowerConsum",
y_label="Stromverbrauch [MW]",
x_label="Jahre"
)
plot_by_group(
cleaned_power_consum,
group_name = "Weekday",
file_name = "plots\weekday_boxplot.png",
colors = week_colors,
title = "Übersicht der einzelnen Wochentage",
y = "PowerConsum",
y_label="Stromverbrauch [MW]",
x_label="Jahre"
)
plot_by_group(
cleaned_power_consum,
group_name = "WorkDay",
file_name = "plots\workday_boxplot.png",
colors = working_colors,
title = "Übersicht, ob Feiertag (FALSE) oder Werktag (TRUE)",
y = "PowerConsum",
y_label="Stromverbrauch [MW]",
x_label="Jahre"
)
plot_by_column(
df = cleaned_power_consum,
x = "Hour",
y = "PowerConsum",
x_label = "Stunden",
y_label = "Stromverbrauch [MW]",
file_name = "plots\hour_boxplot.png",
title = "Übersicht der einzelnen Stunden"
)
plot_by_column(
df = cleaned_power_consum,
x = "Month",
y = "PowerConsum",
x_label = "Monate",
y_label = "Stromverbrauch [MW]",
file_name = "plots\month_boxplot.png",
title = "Übersicht der einzelnen Monate"
)
plot_by_column(
df = cleaned_power_consum,
x = "Week",
y = "PowerConsum",
x_label = "Woche",
y_label = "Stromverbrauch [MW]",
file_name = "plots\week_boxplot.png",
title = "Übersicht der einzelnen Wochen"
)
plot_by_column(
df = cleaned_power_consum,
x = "Year",
y = "PowerConsum",
x_label = "Jahr",
y_label = "Stromverbrauch [MW]",
file_name = "plots\year_boxplot.png",
title = "Übersicht der einzelnen Jahre"
)
plot_year_month_week_day(
df=cleaned_power_consum,
date_column="DateIndex",
y="PowerConsum",
from_year=2015,
to_year=2024,
from_week=0,
to_week=53,
year_for_week=2018,
from_day=1,
to_day=30,
month_for_day=4,
year_for_day=2018,
from_month=1,
to_month=12,
year_for_month=2018,
holiday="Holiday",
day_of_week = "Weekday"
)
다음 섹션에서는 데이터에 대해 점점 더 자세히 설명합니다. 여기서는 연간 표현부터 시작하겠습니다.
그림 2는 2015~2024년의 연간 표현입니다. 여기서 우리는 연초에 전력 소비가 증가하고 연말(크리스마스, 신년)에는 전력 소비가 감소한다는 것을 알 수 있습니다. 전체적으로 웃는 모양이나 활 모양처럼 보입니다.
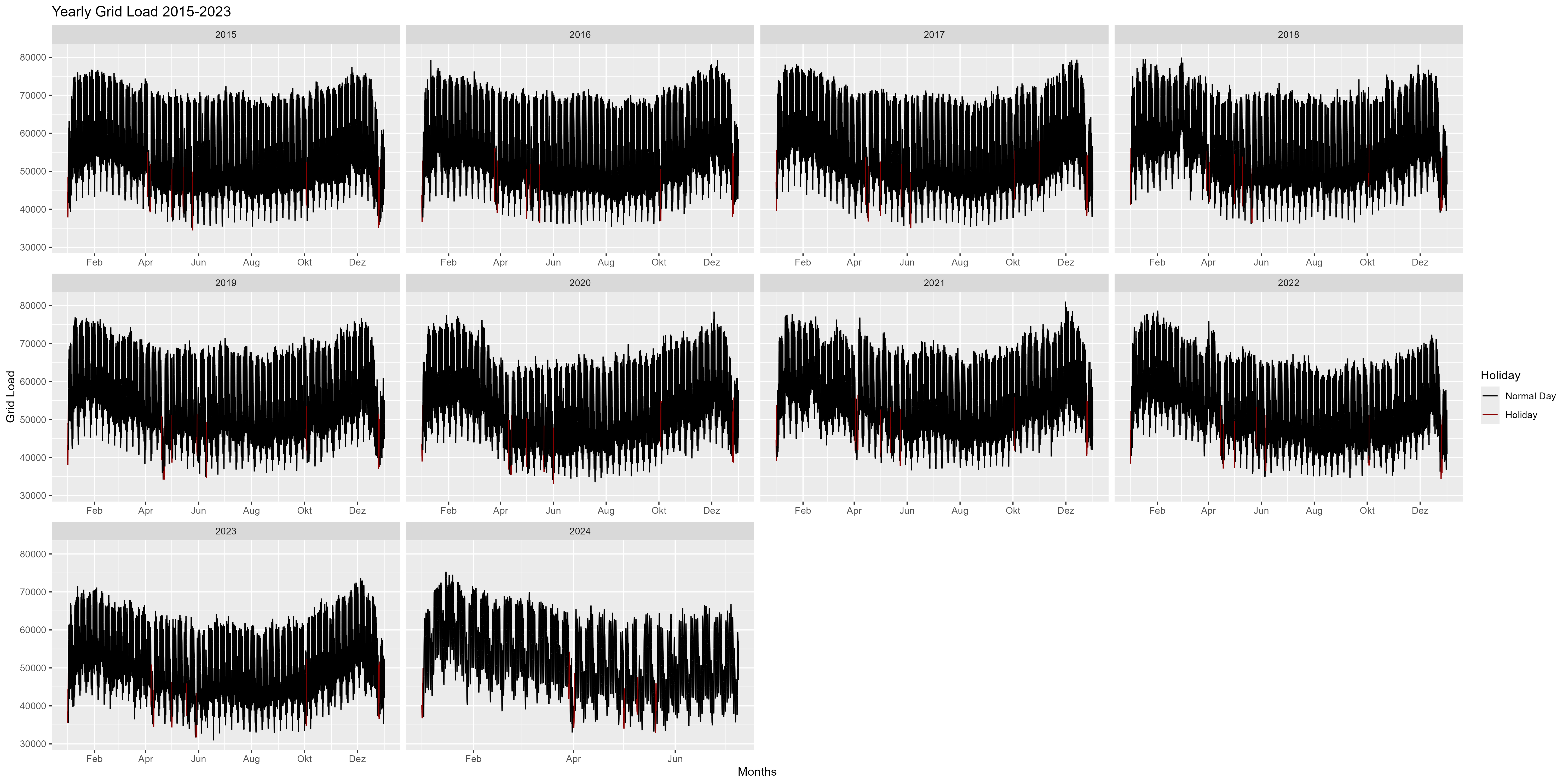그림 2 전력 소비량, 매년 단일 측면으로
모든 연도를 집계하여 몇 주로 나누어 보겠습니다. 그림 3의 상자 그림은 모든 연도를 결합합니다. 패턴을 더 자세히 볼 수 있습니다. 한 해의 시작과 끝은 붉은색으로 표현되어 일반적인 '스마일 모양'에서 감소하는 모습을 보입니다.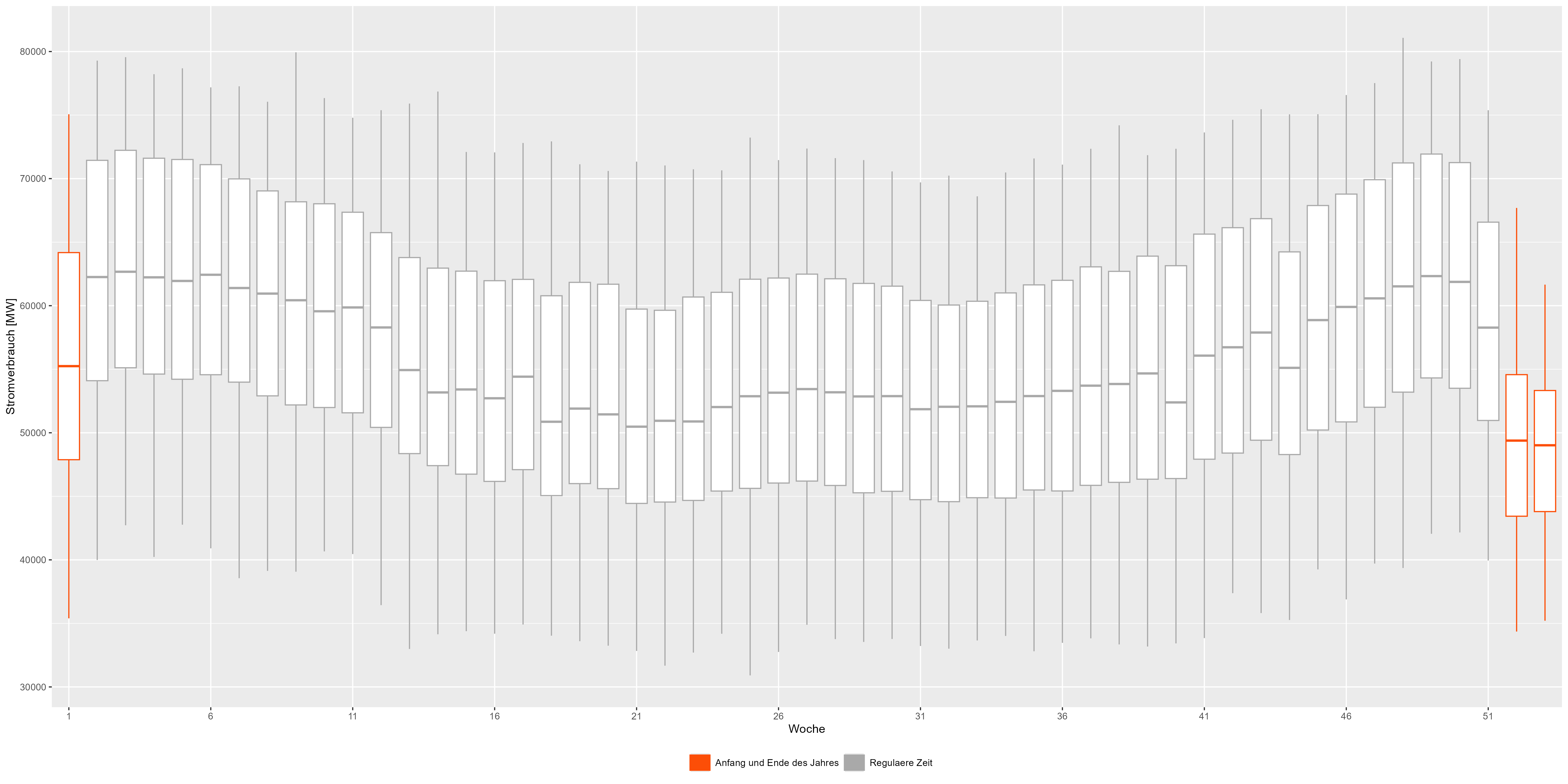
그림 3 전력 소비 주간 집계 데이터
좀 더 자세히 살펴보고 2018년을 예로 들어 살펴보겠습니다. 그림 4는 2018년의 월별 표현입니다. 여기서 우리는 연말을 더 자세히 관찰할 수 있습니다. 12월 24일경에 전력 소모량이 감소합니다. 여기서도 주목할만한 것은 주말과 공휴일(빨간색)입니다. 모든 주말과 모든 공휴일에는 감소합니다.
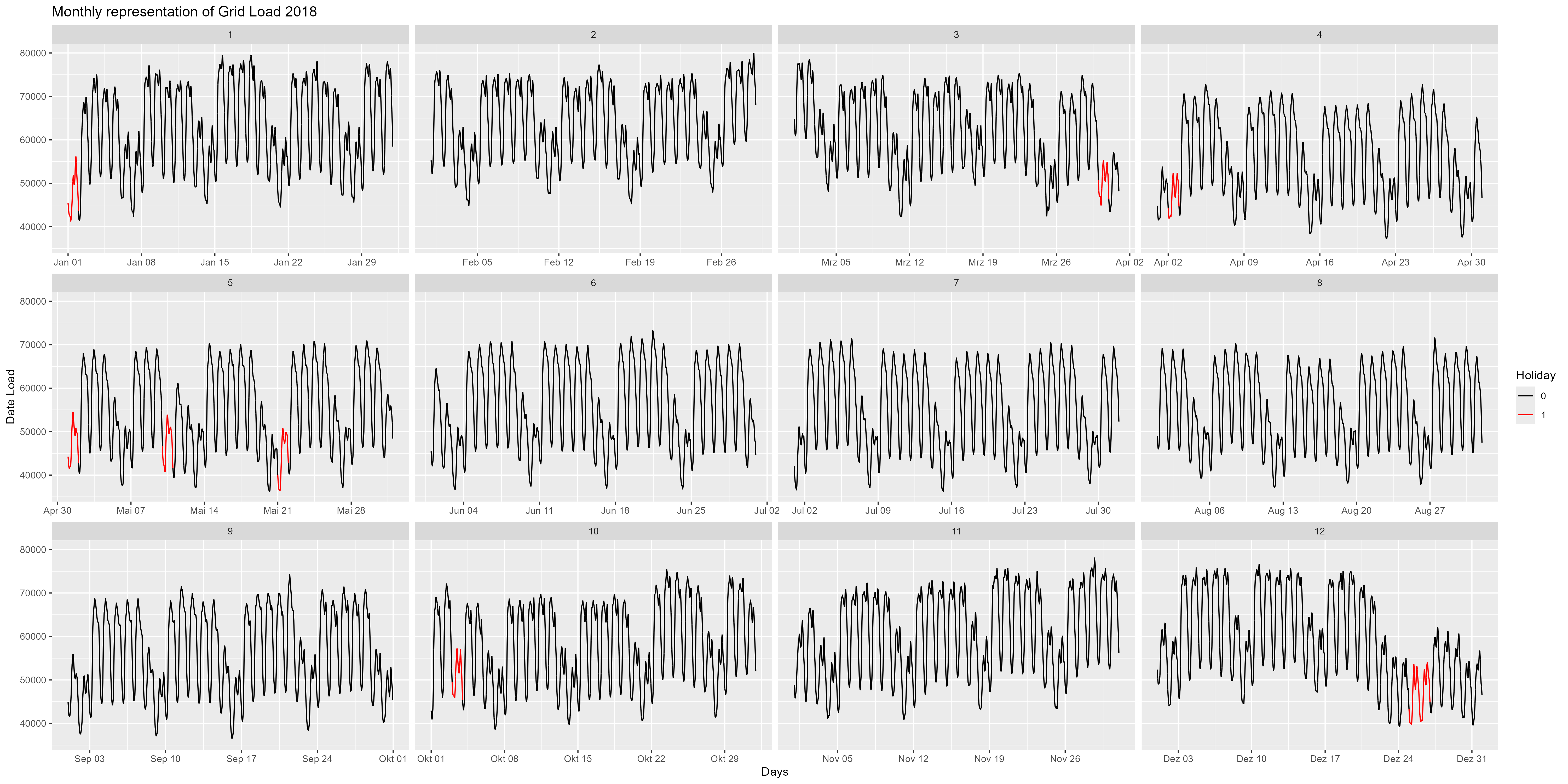그림 4 매월 단일 측면으로 나타낸 전력 소비량
더 나아가서 시간별 데이터 표현을 확인할 수도 있습니다. 그림 5는 매 시간마다 집계된 상자 그림을 보여줍니다. 야간(21:00~06:00)도 감소하고, 주간/근무시간(06:00~21:00)은 증가합니다. 또한 모델에 포함되어야 하는 패턴입니다.
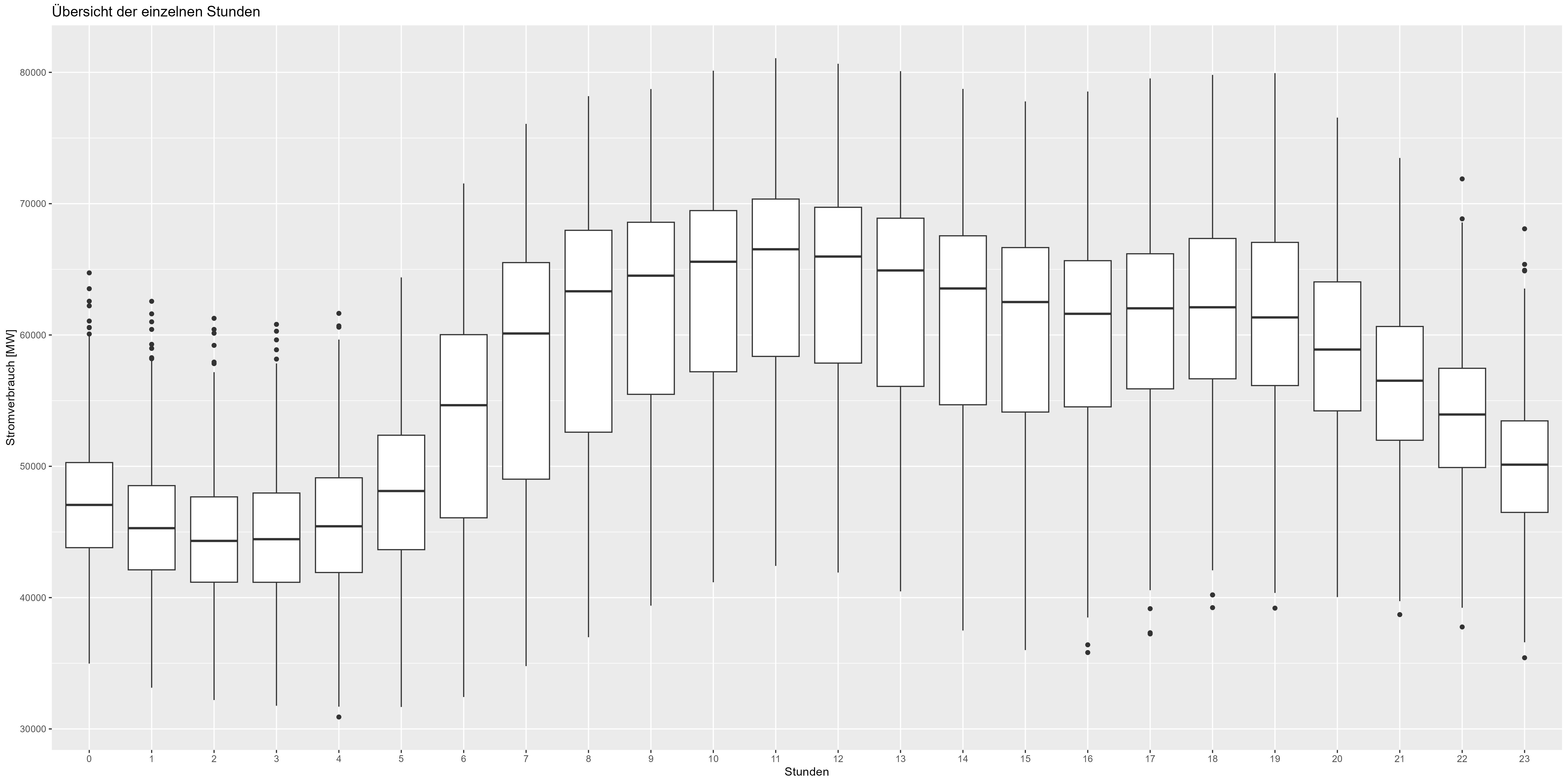그림 5 전력 소비 시간별 집계 데이터
평일에 대해 이야기 해 봅시다. 예상대로 주말에는 전력 소비가 감소합니다. "Durchschnitt"가 평균입니다. 그림 6은 지난 몇 년간의 모든 평일(집계)을 보여줍니다. 주말에는 약 10,000MW 정도 감소합니다.
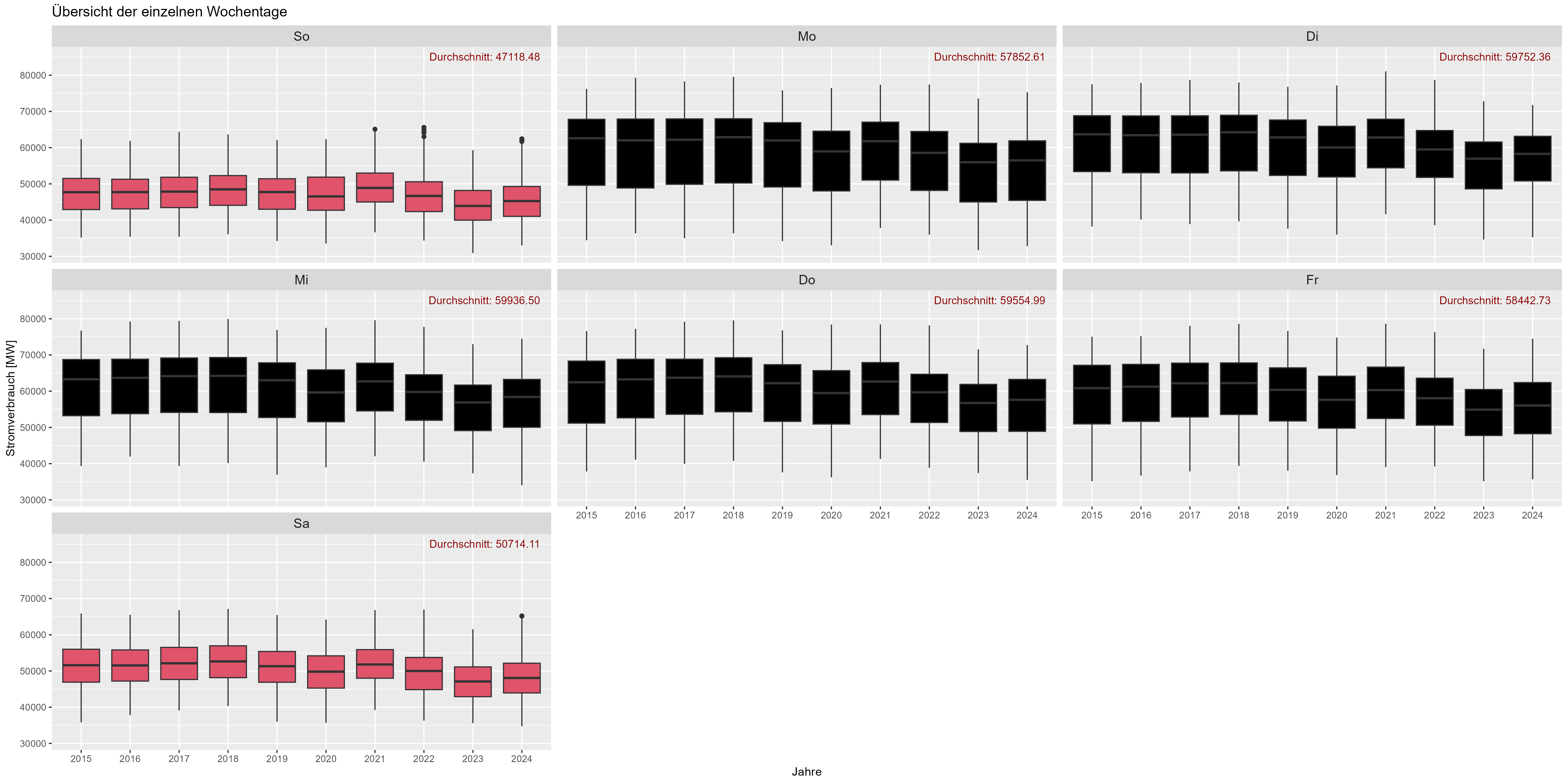그림 6 전력 소비 "요일 효과"
그림 8은 휴일 효과를 보여줍니다. "Durchschnitt"는 수년간의 평균 전력 소비량입니다. 휴일(빨간색)에 비해 "근무일"(진한 회색)의 전력 소비가 크게 증가합니다. 여기서 우리는 휴일이 전력 소비의 주말과 같다고 가정할 수 있습니다."
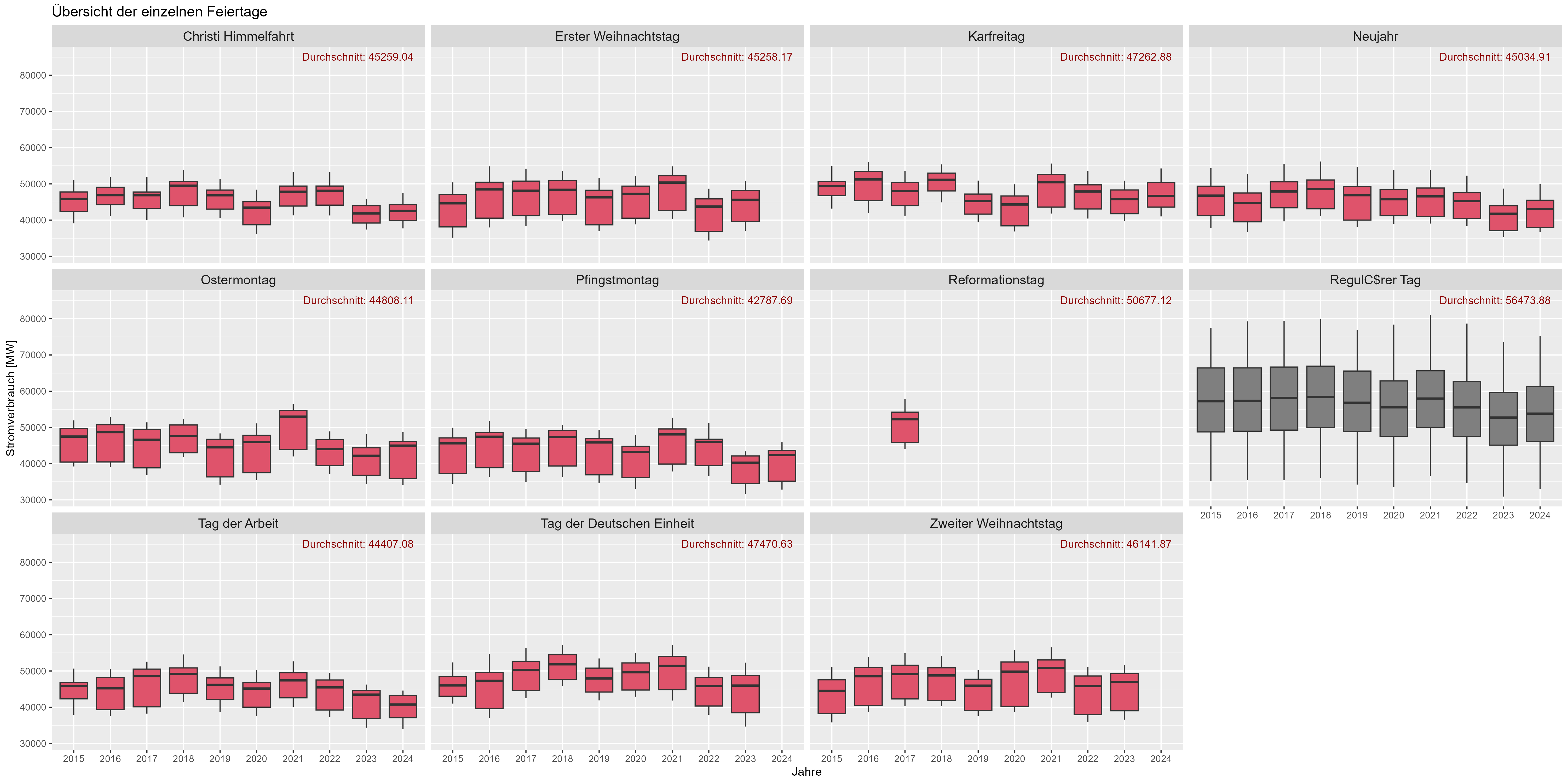그림 6 전력 소비 "휴일 효과"
그림 7은 날짜별 다양한 행동을 나타냅니다. 4가지 카테고리가 있습니다. "Feiertag Kein Wochenende"는 휴일이지만 주말이 아니라는 뜻입니다. "Feiertag Wochenende"는 휴일이자 주말이라는 뜻입니다. "Kein Feiertag Kein Wochenende"는 정규 근무일을 의미하고 "Kein Feiertag Wochenende"는 주말만 의미합니다. 가정된 바와 같이 정규 근무일이 아닌 경우에도 유사한 분포를 관찰할 수 있습니다.
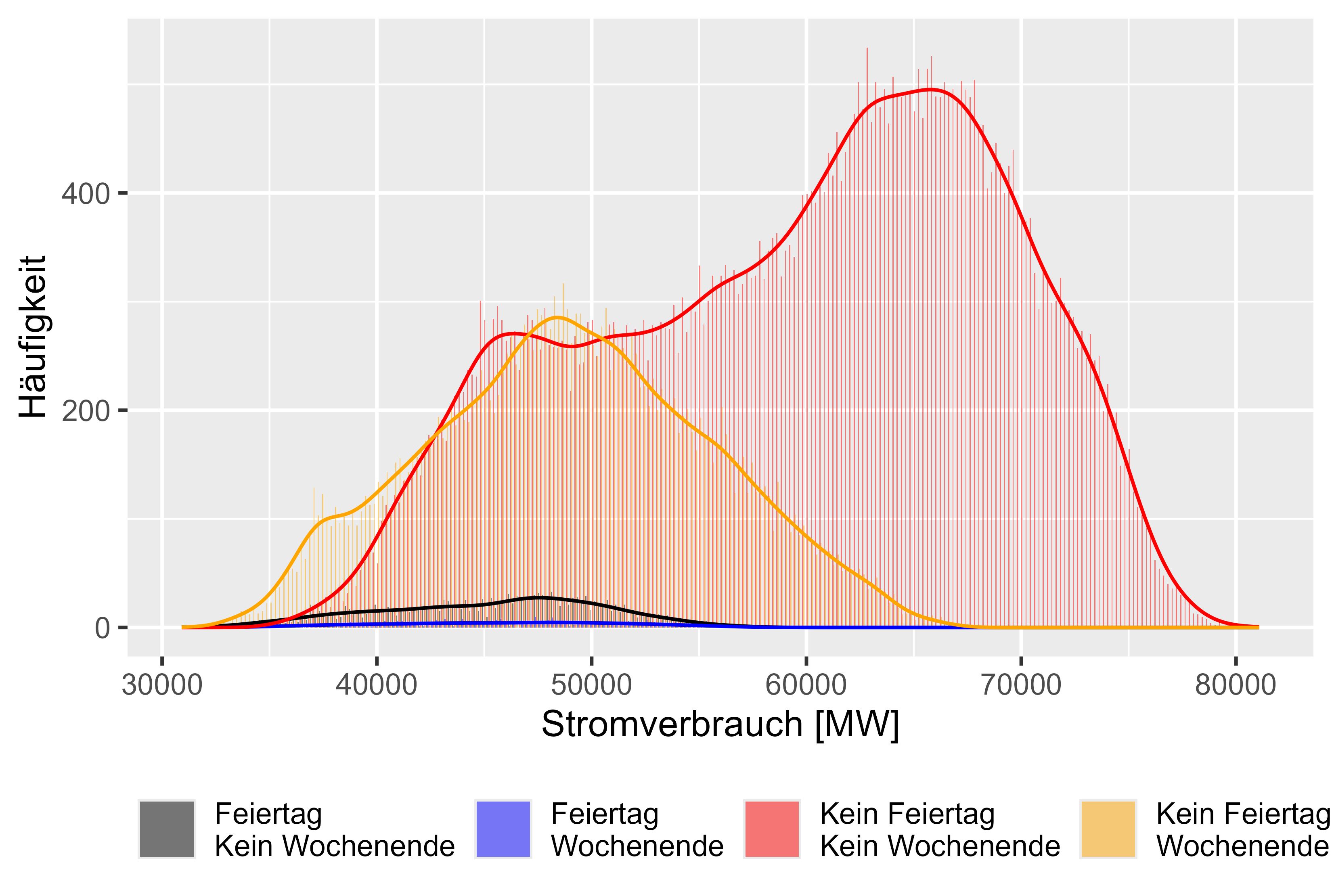그림 7 전력 소비 "다른 효과" 비교
MeanLastTwoDays, MeanLastWeek, MaxLastOneDay 및 MinLastOneDay와 같은 지연된 값은 생성된 기능입니다.
DOI에서 설명한 것과 유사: 10.1109/TPWRS.2011.2162082 - 반모수적 추가 모델을 기반으로 한 단기 부하 예측
그림 8-11(빨간색은 근무일이 아님)은 실제 전력 소비량에 비해 지연된 값을 나타냅니다.
이렇게 생성된 특징에는 가벼운 상관관계가 있습니다.
# Check Correlation
cor <- cor(cleaned_power_consum[sapply(cleaned_power_consum, is.numeric)], method = c("pearson", "kendall", "spearman"), use = "complete.obs")
| 특징 | PowerConsum과의 상관관계 |
|---|---|
| 휴일 스무딩 | -0.556194 |
| 지난 주 평균 | 0.389044 |
| 평균 지난 2일 | 0.201253 |
| 최대지난1일 | 0.320193 |
| 최소최근1일 | 0.348583 |
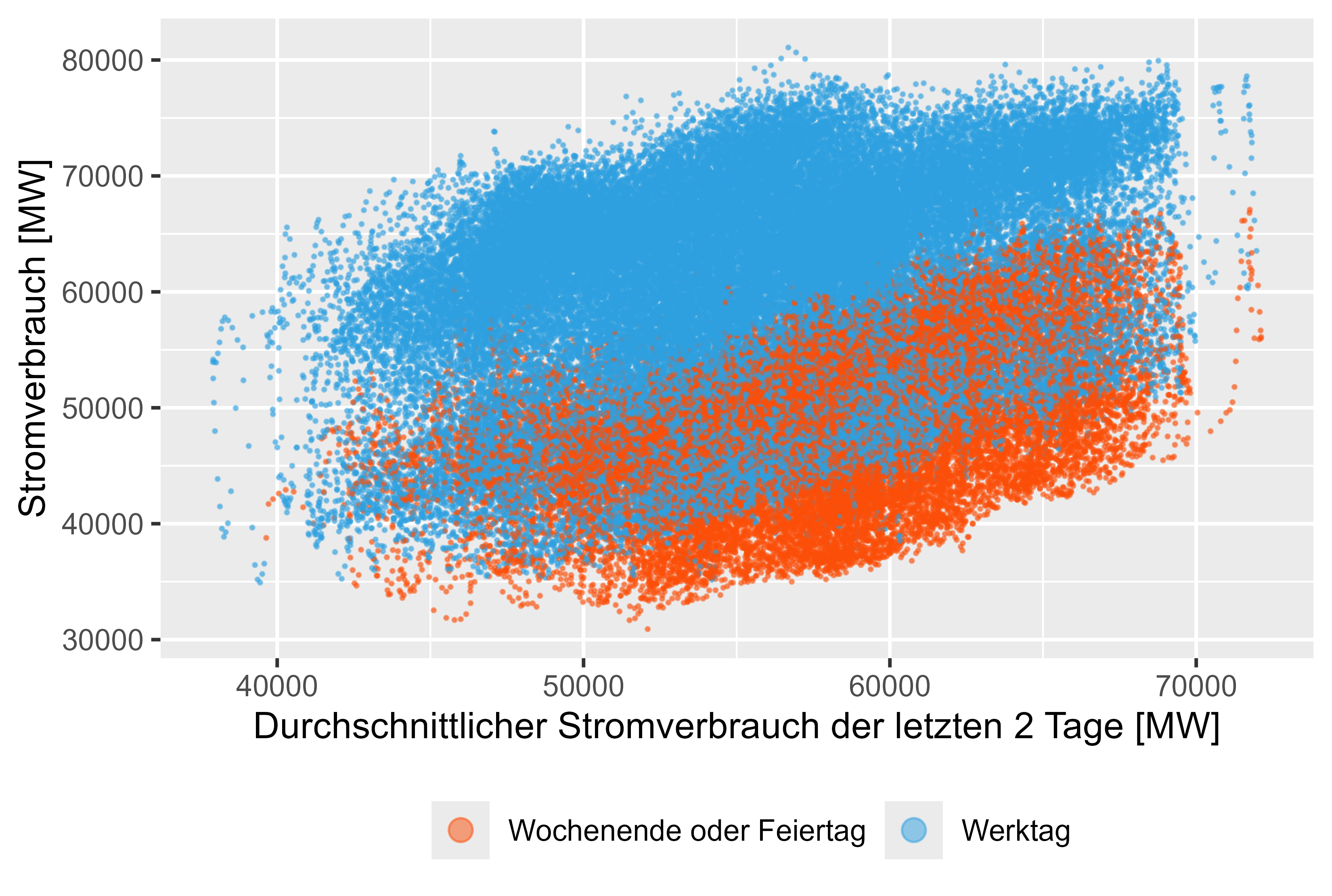그림 8 전력 소비 - MeanLastTwoDays
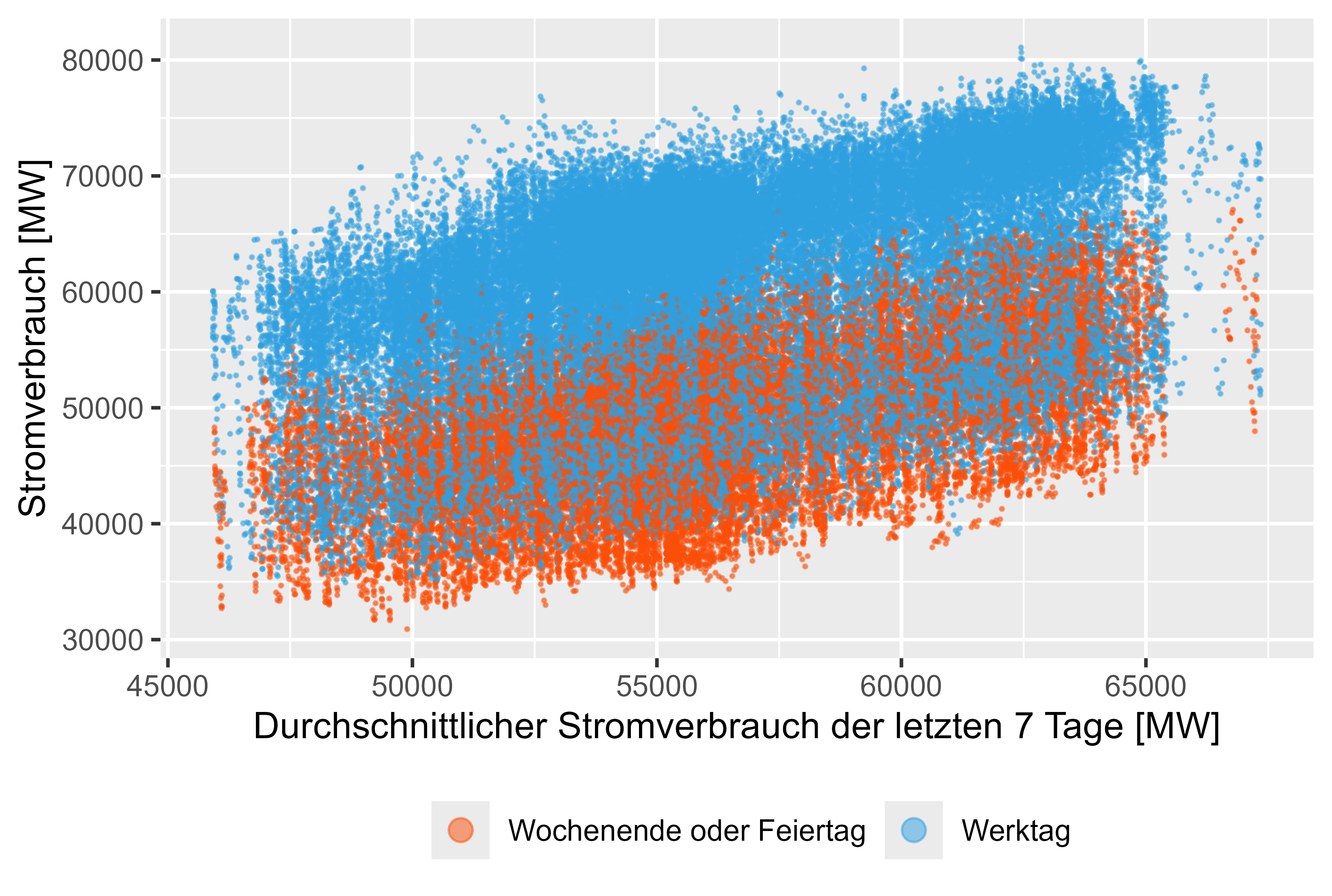그림 9 전력 소비 - MeanLastWeek
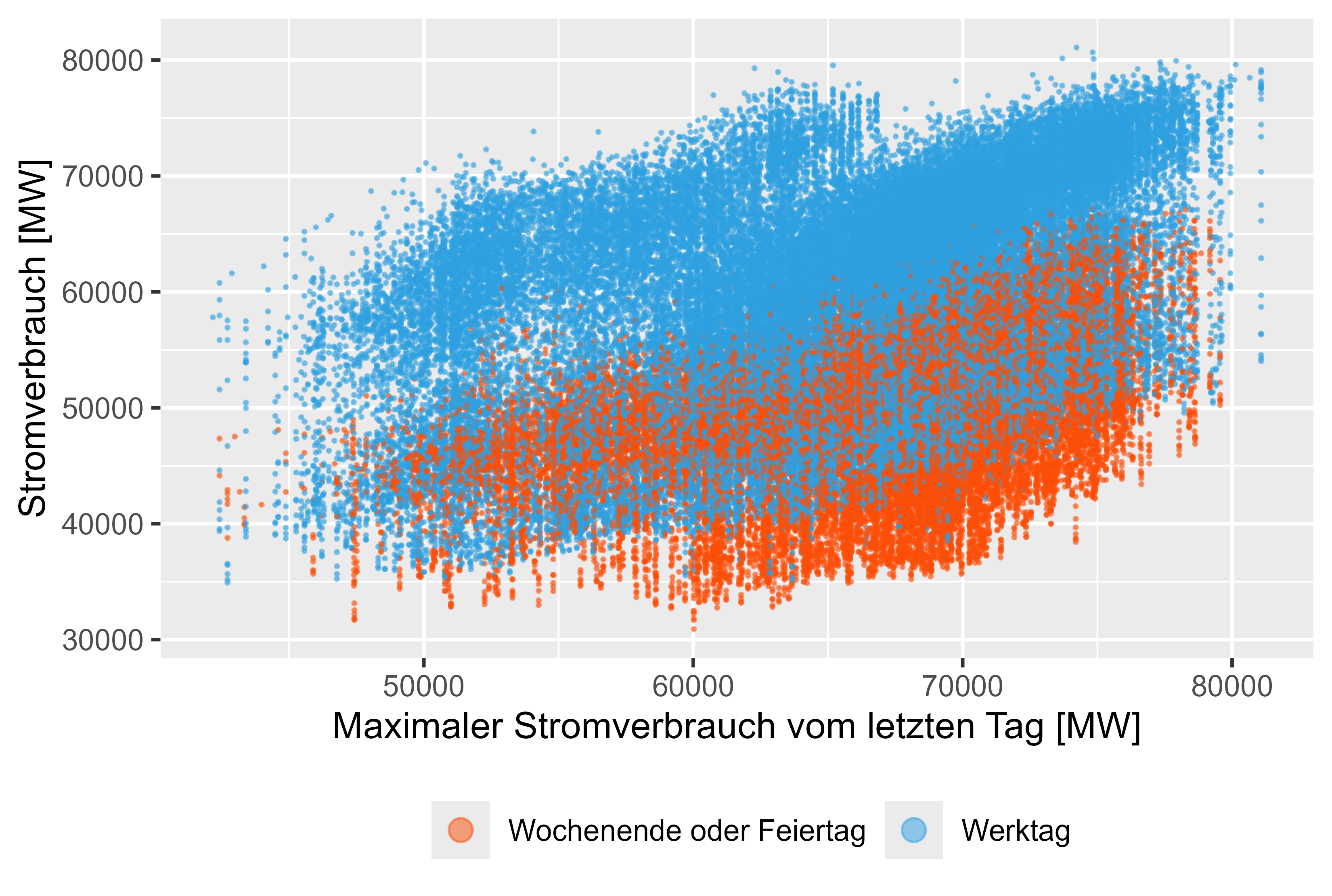그림 10 전력 소비 - MaxLastOneDay
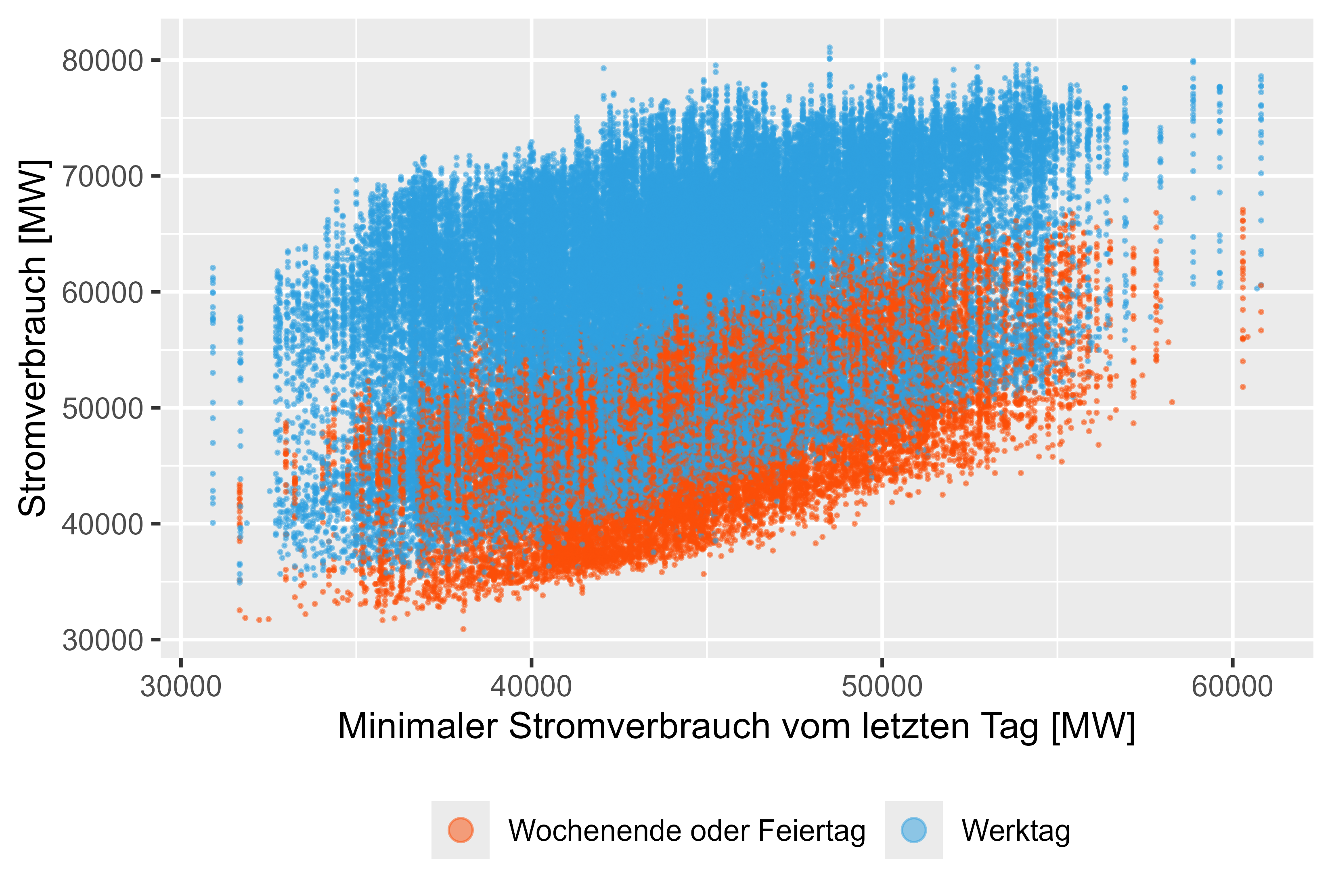그림 11 전력 소비 - MinLastOneDay
복잡한 계절성이 있습니다. 시간별 해결에는 연간, 주간 및 일일 계절성이 있습니다. 모델에서 추적해야 하는 항목입니다. 여기서의 해결책은 예측: 원리 및 실습 12.1장 복잡한 계절성에서 논의된 바와 같이 푸리에 용어를 사용하여 cos() 및 sin()을 통해 복잡한 계절성을 표현하고 조합하는 것입니다.
ACF 및 PACF 플롯을 조금 살펴보면 눈에 띄는 스파이크는 거의 없지만 96개의 지연된 값을 나타내는 것일 뿐입니다. 1년 동안 ~9000개의 지연된 관측을 취한다면 복잡한 계절성이 있을 것입니다. 이것이 푸리에 항을 사용하는 것이 더 쉬운 이유입니다. 또한 PDQ 및 pdq 구성 요소를 찾는 것만으로는 제대로 작동하지 않았습니다.
ARIMA(...
stepwise=FALSE,
greedy=FALSE,
approx=FALSE)
그 자체. 또한 푸리에 항이 없으면 훈련 시간이 극적으로 늘어납니다.
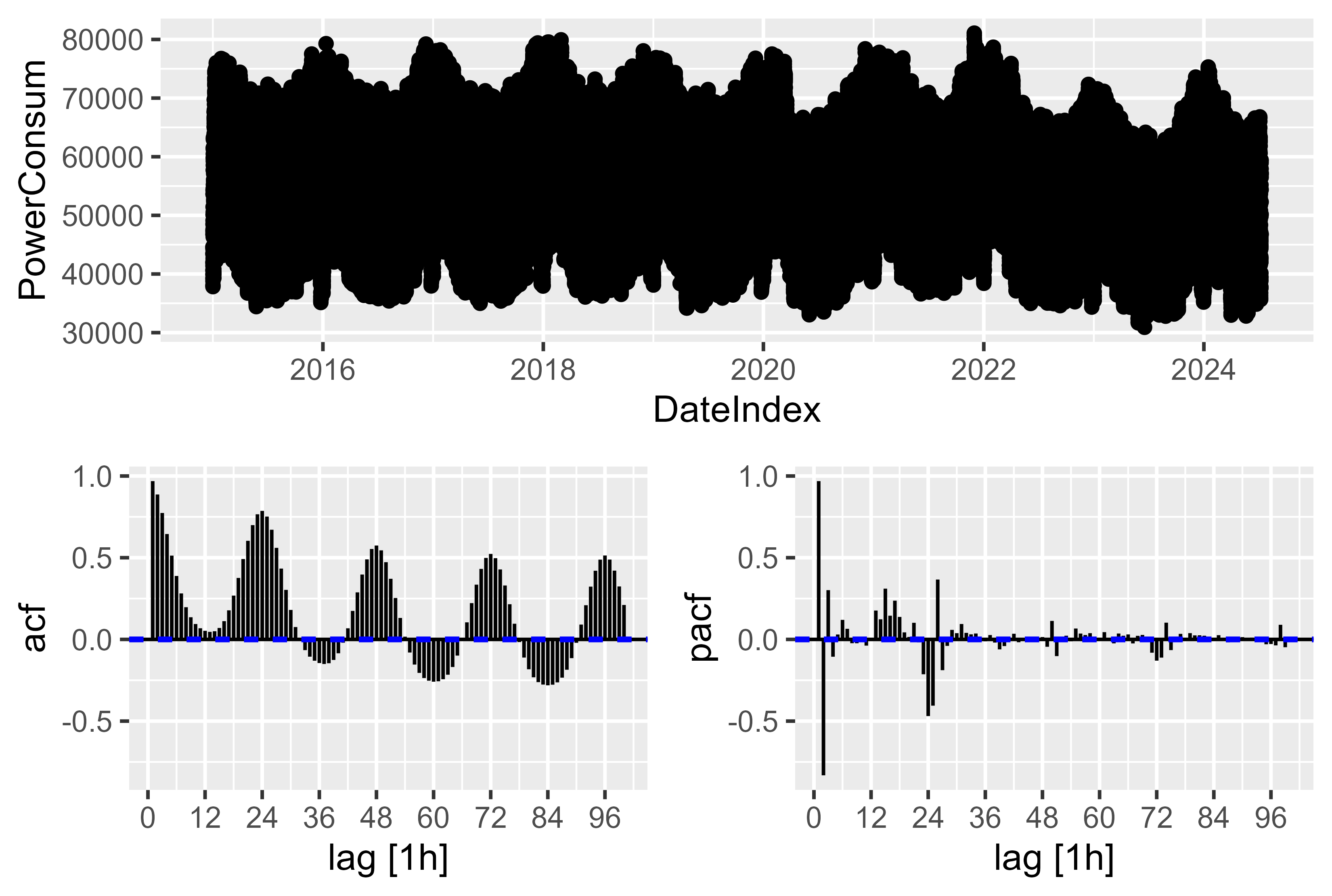그림 12 전력 소비 - ACF PACF 원시 전력 소비 도표
이 작업에서 발견된 최고의 기능 조합은 다음과 같습니다.
모델을 비교하기 위해 메트릭 MAE 및 MAPE를 사용합니다. SMARD는 SMARD 페이지의 "Bundesnetzagentur" 모델입니다. 선지자 모델도 시험해 보았고 성능은 좋았지만 충분하지 않았습니다.
SMARD 예측 값은 MAPE 3.6%에 도달했습니다. <- 이 연구에는 포함되어 있지 않습니다.
훈련 데이터:
지금까지 발견된 최고의 모델 전쟁 LHM + DHR(선형-조화 모델 + 동적-조화-회귀)
아이디어는 ARIMA 모델과 선형 모델을 앙상블하는 것입니다. ARIMA 모델이 휴일에 더미 변수를 처리하기가 어려웠기 때문입니다. 그래서 앙상블 모델이 도움이 되었습니다.
train_power_consum <- cleaned_power_consum |>
filter(year(DateIndex) > 2020 & (year(DateIndex) < 2024))
generate_models(model_name = "model/mean_naive_drift",
train_power_consum = train_power_consum)
train_power_consum_v5 <- train_power_consum |>
mutate(HolidaySmoothed = Holiday + sin(2 * pi * (as.numeric(Hour)+1) / 24))
holiday_effect_model <- lm(
PowerConsum ~
HolidaySmoothed,
data = train_power_consum_v5
)
saveRDS(holiday_effect_model, file = "ensemble_model/version_5/holiday_effect_2021_2023.rds")
train_power_consum_v5$Residuals <- residuals(holiday_effect_model)
fit <- train_power_consum_v5 |>
model(
ARIMA = ARIMA(Residuals ~
PDQ(0,0,0)
+ pdq(d=0)
+ MeanLastWeek
+ WorkDay
+ EndOfTheYear # new
+ FirstWeekOfTheYear # new
+ MeanLastTwoDays
+ MaxLastOneDay
+ MinLastOneDay
+ fourier(period = "day", K = 6)
+ fourier(period = "week", K = 7)
+ fourier(period = "year", K = 3)
)
)
saveRDS(fit, file = "ensemble_model/version_5/arima_2021_2023.rds")
효과와 모델 작동 방식을 시각화할 수 있었습니다. 그림 13은 이 모델의 기본 아이디어를 보여줍니다. 먼저 LHM 모델을 피팅하고 잔차를 계산합니다. 잔차로 DHR 모델을 훈련하고 둘을 합산합니다. 그것은 LHM의 일종의 거울이며 값을 다시 맨 위로 밀어 넣습니다.
LHM 모델의 경우 여기서는 24시간마다 반복되고 휴일이나 근무일에 감소하거나 증가하는 동 곡선이라는 간단한 접근 방식을 사용합니다.
새로운 데이터에 대한 LHM을 예측함으로써 우리는 새로운 데이터에 대한 잔차를 예측할 수 있습니다. 잔차 + LHM은 값을 "올바른" 위치로 다시 이동합니다.
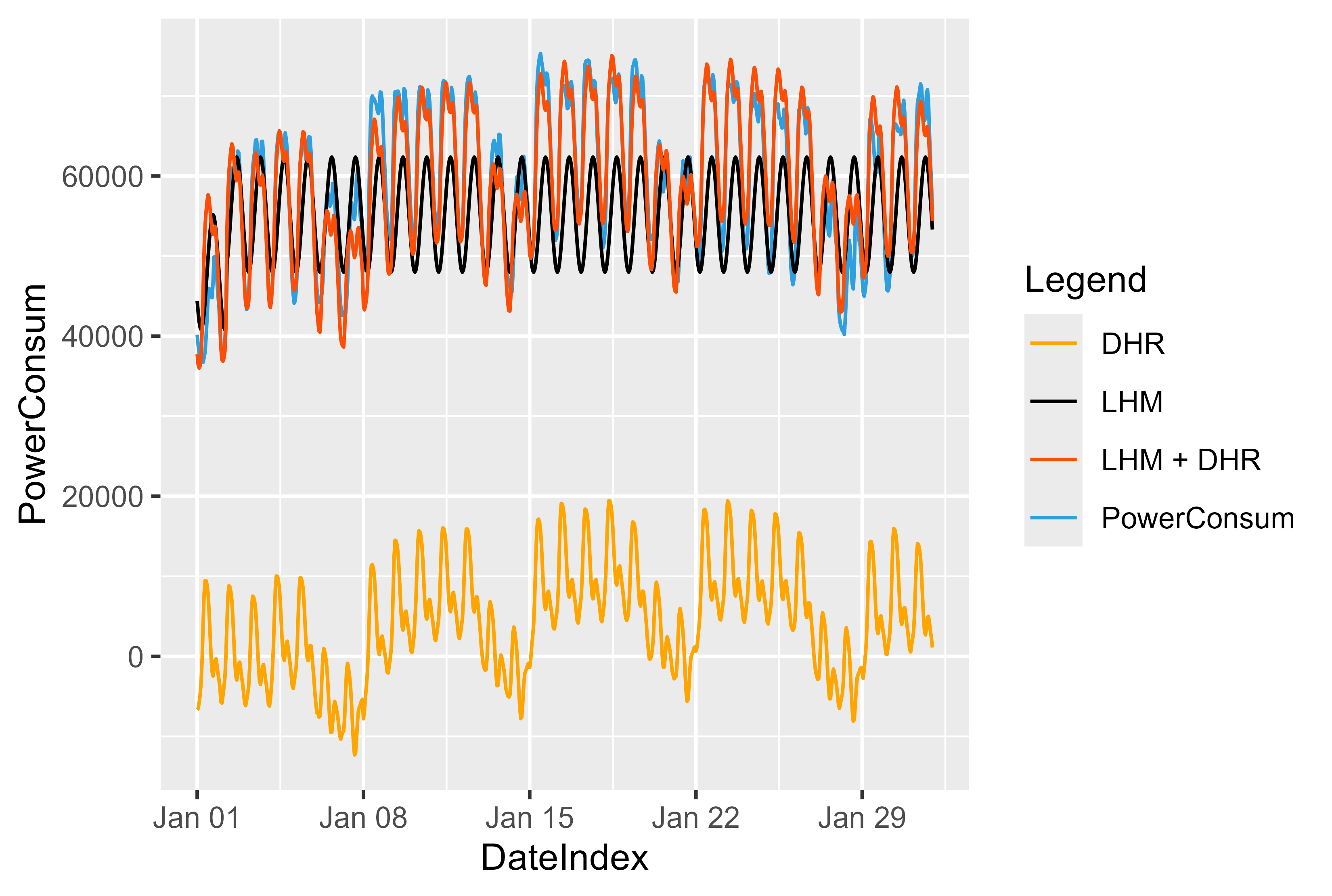그림 13 LHM + DHR 모델 표현
ensembled_fc <- load_ensembled_models(
days_to_forecast = 40,
months_to_forecast = 6,
year_to_forecast = 2024,
starting_month = 1,
real_data = cleaned_power_consum,
smard_fc = cleaned_smard_pred,
model_path = "ensemble_model"
)
all_forecasts_ensembled <- ensembled_fc$all_forecasts
raw_fc_ensembled <- ensembled_fc$raw_forecasts
fc <- load_all_model_results(
days_to_forecast = 40,
months_to_forecast = 6,
year_to_forecast = 2024,
starting_month = 1,
smard_fc = cleaned_smard_pred,
real_data = cleaned_power_consum
)
all_forecasts <- fc$combined_forecasts
raw_fc <- fc$raw_forecasts
metric_results <- calculate_metrics(fc_data = all_forecasts, fc_data_ensembled=all_forecasts_ensembled)
# Plot best Model for single Models
name_of_best_model_for_single_model <- plot_forecast(
all_forecasts = all_forecasts,
metric_results = metric_results,
cleaned_power_consum = cleaned_power_consum,
raw_fc = raw_fc,
month_to_plot = 1,
days_to_plot = 40
)
# Plot best Model for ensembled Models
name_of_best_model_ensembled <- plot_forecast_ensembled(
all_forecasts = all_forecasts_ensembled,
metric_results = metric_results,
cleaned_power_consum = cleaned_power_consum,
month_to_plot = 1,
days_to_plot = 40
)
# Residuals Compared with SMARD
plot_compare_with_smard(
all_forecasts = all_forecasts_ensembled,
name_of_best_model = name_of_best_model_ensembled
)
# LHM DHM representation
plot_representation_of_lhm_dhm_components(path_dhm = "ensemble_model/version_5/arima_2021_2023.rds",
path_lhm = "ensemble_model/version_5/holiday_effect_2021_2023.rds",
from_month = 1,
to_month = 1,
raw_fc_ensembled = raw_fc_ensembled)
version_5(LHM + DHR 모델)의 경우 MAPE 3.8%라는 확실한 점수를 받았습니다.
ARIMA 모델(arima_14)만 사용한다면 좀 더 자세히 살펴보겠습니다. 그림 14는 이 모델의 결과를 나타냅니다. 공휴일(주황색), 주말(빨간색), 평상시(파란색)를 볼 수 있습니다. ARIMA 모델에 대한 더미 변수가 있더라도 휴일을 올바르게 포착할 수 없었음에도 휴일에는 상당한 이상값이 있습니다.
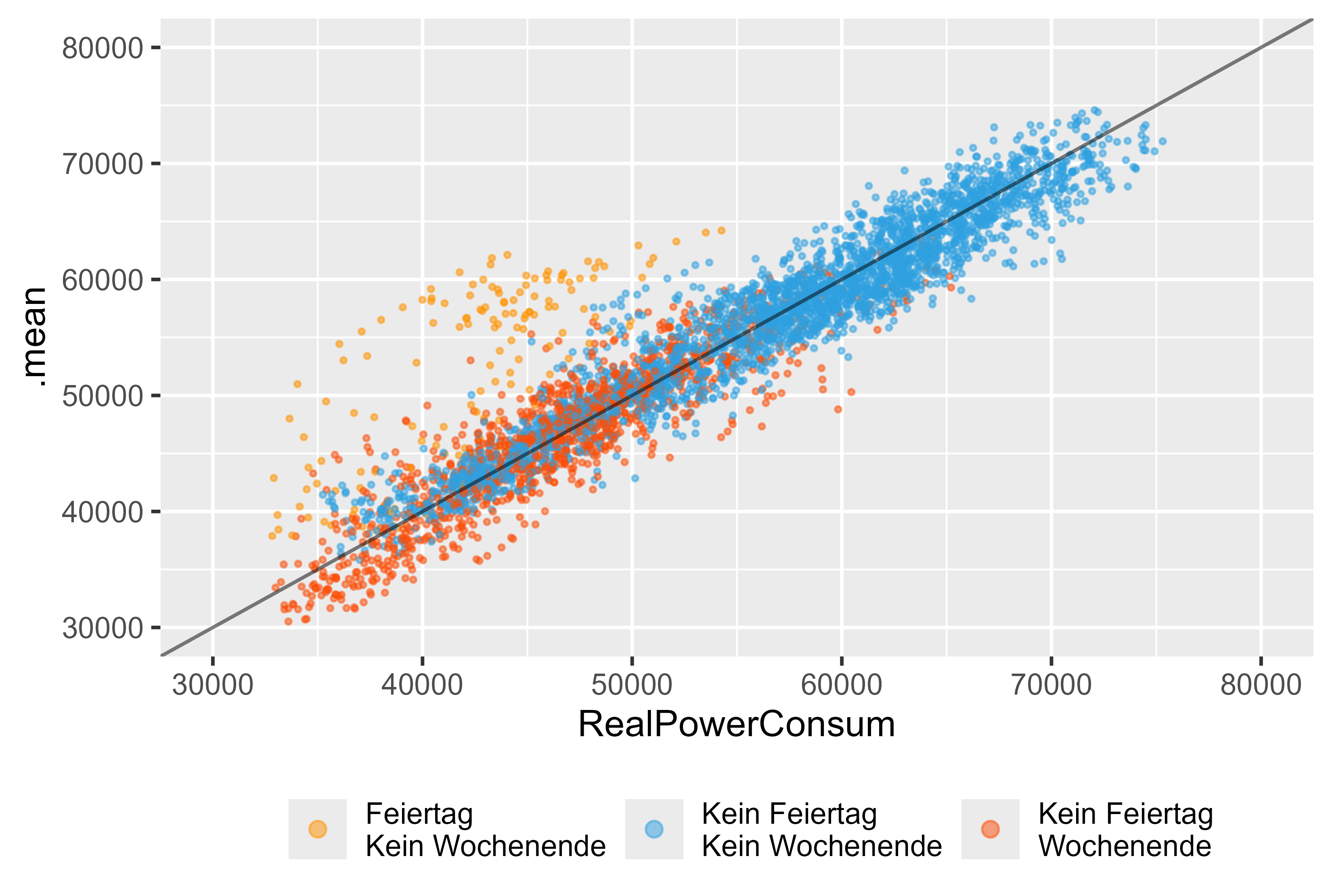그림 14 단일 모델로서의 예측 값과 실제 값 ARIMA(DHR, arima_14)
반면에 LHM + DHR 모델은 휴일에 더 나은 성능을 보여줍니다. 그림 15는 이를 나타냅니다.
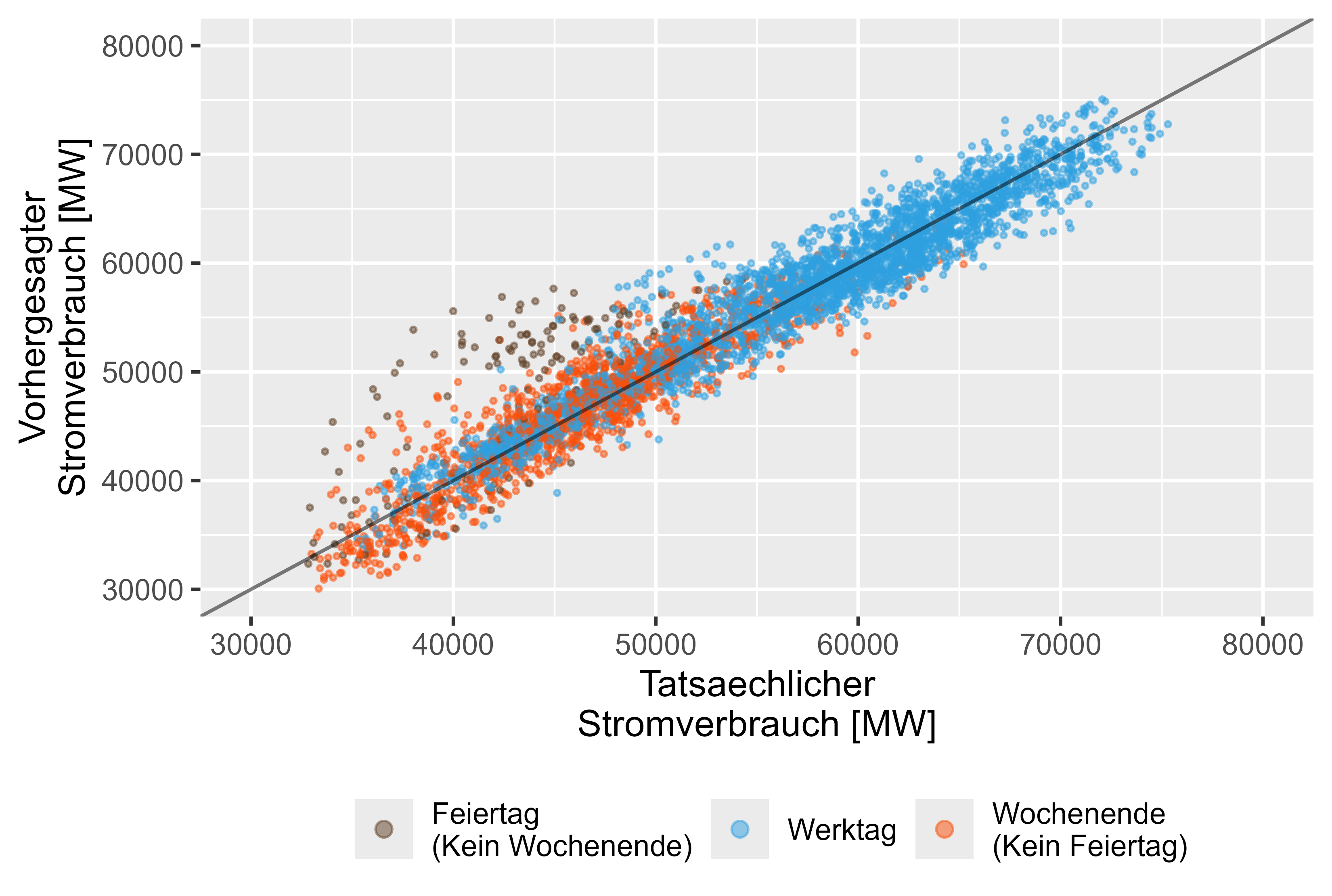그림 15 예측 값과 실제 값 LHM + DHR, 앙상블 모델
그림 16은 2024년 1월의 예측을 보여줍니다. 합리적으로 보입니다.
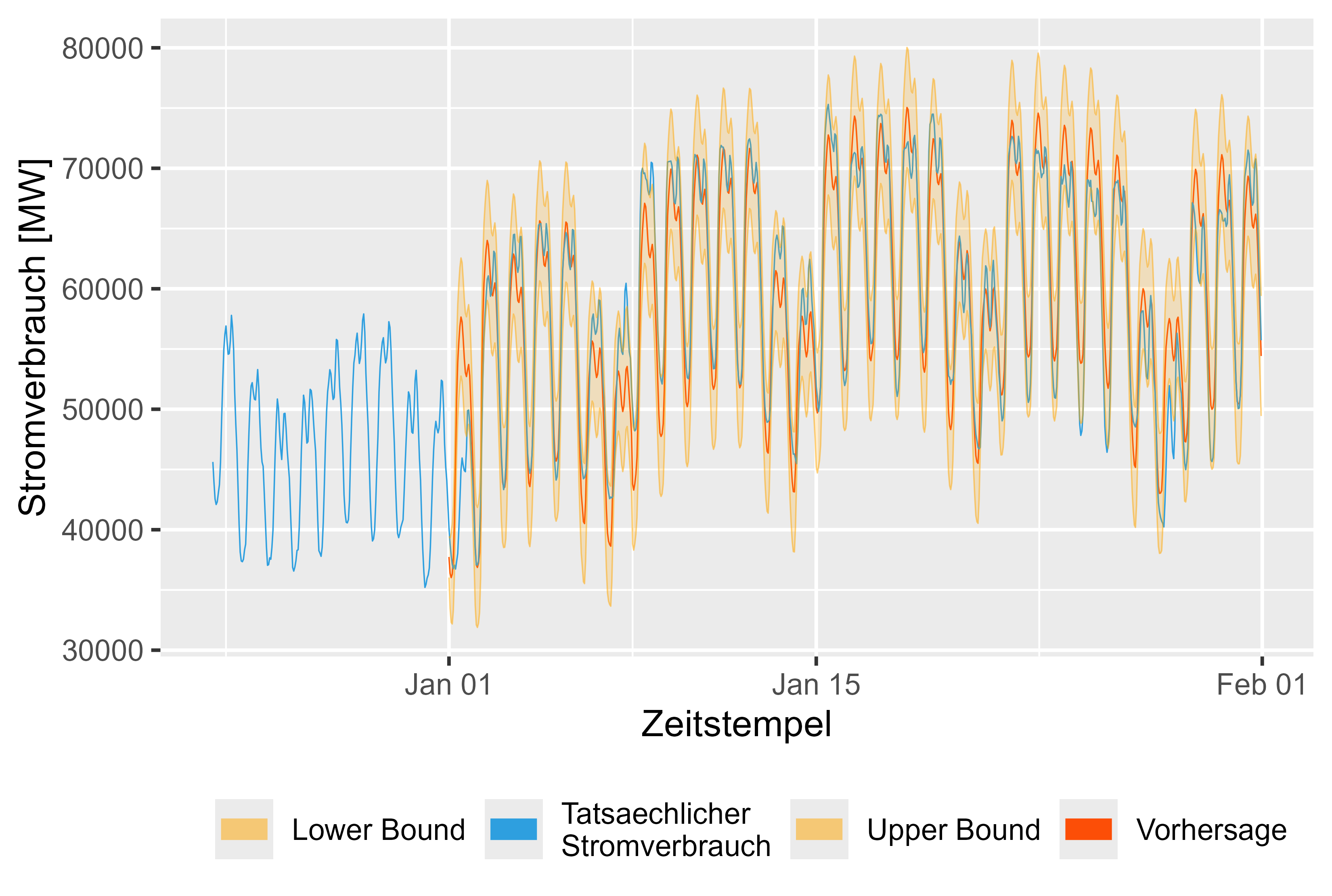그림 16 2024년 1월 LHM + DHR 예측 값과 실제 값
또한 SMARD 모델과 비교하여 모델의 잔차가 괜찮아 보입니다. 스파이크가 거의 없으며 이는 중요할 수 있으며 모델링을 통해 더 잘 준비될 수 있습니다. 그러나 전반적으로 견고한 결과입니다.
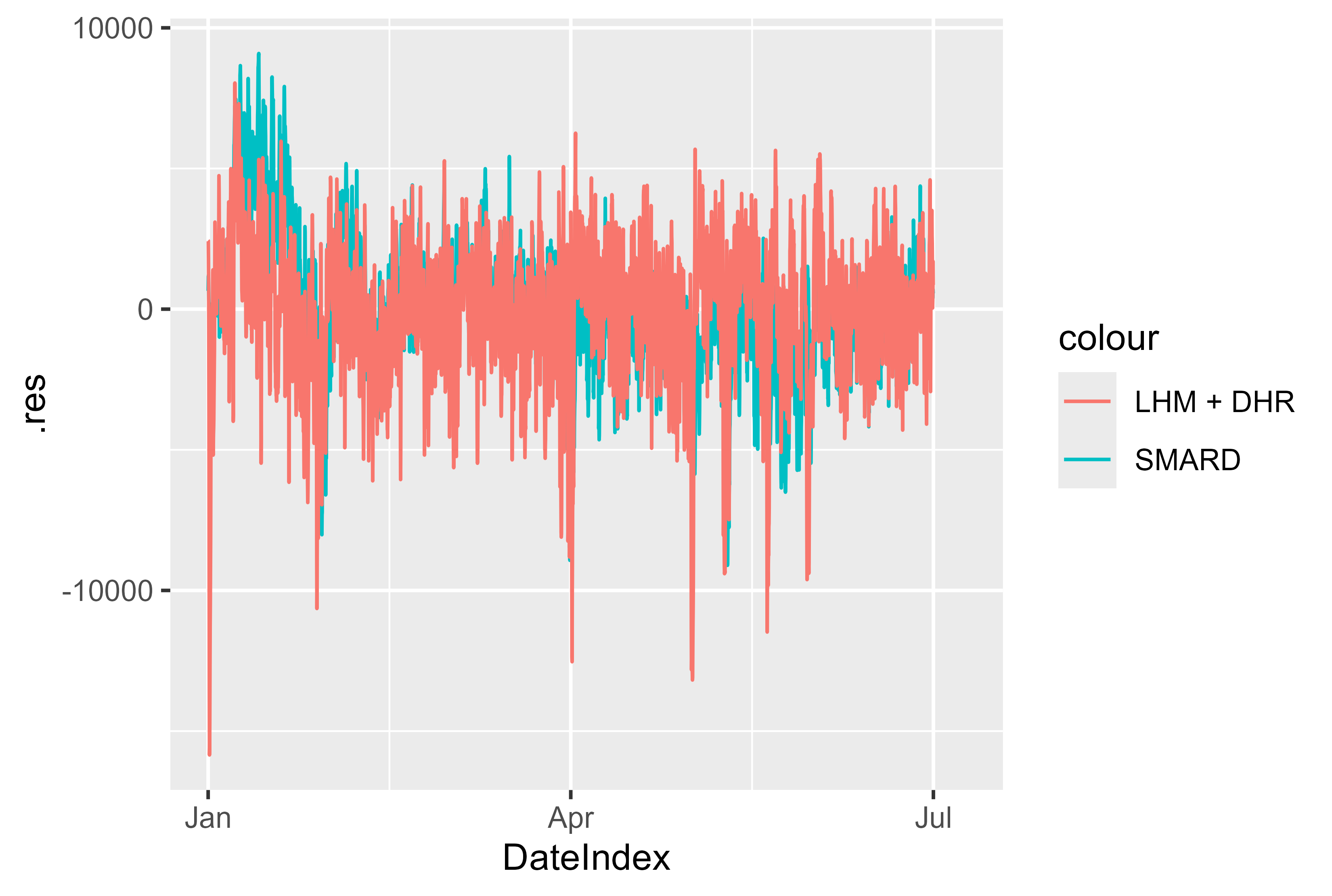그림 17 2024년 1월~7월의 잔차 LHM + DHR
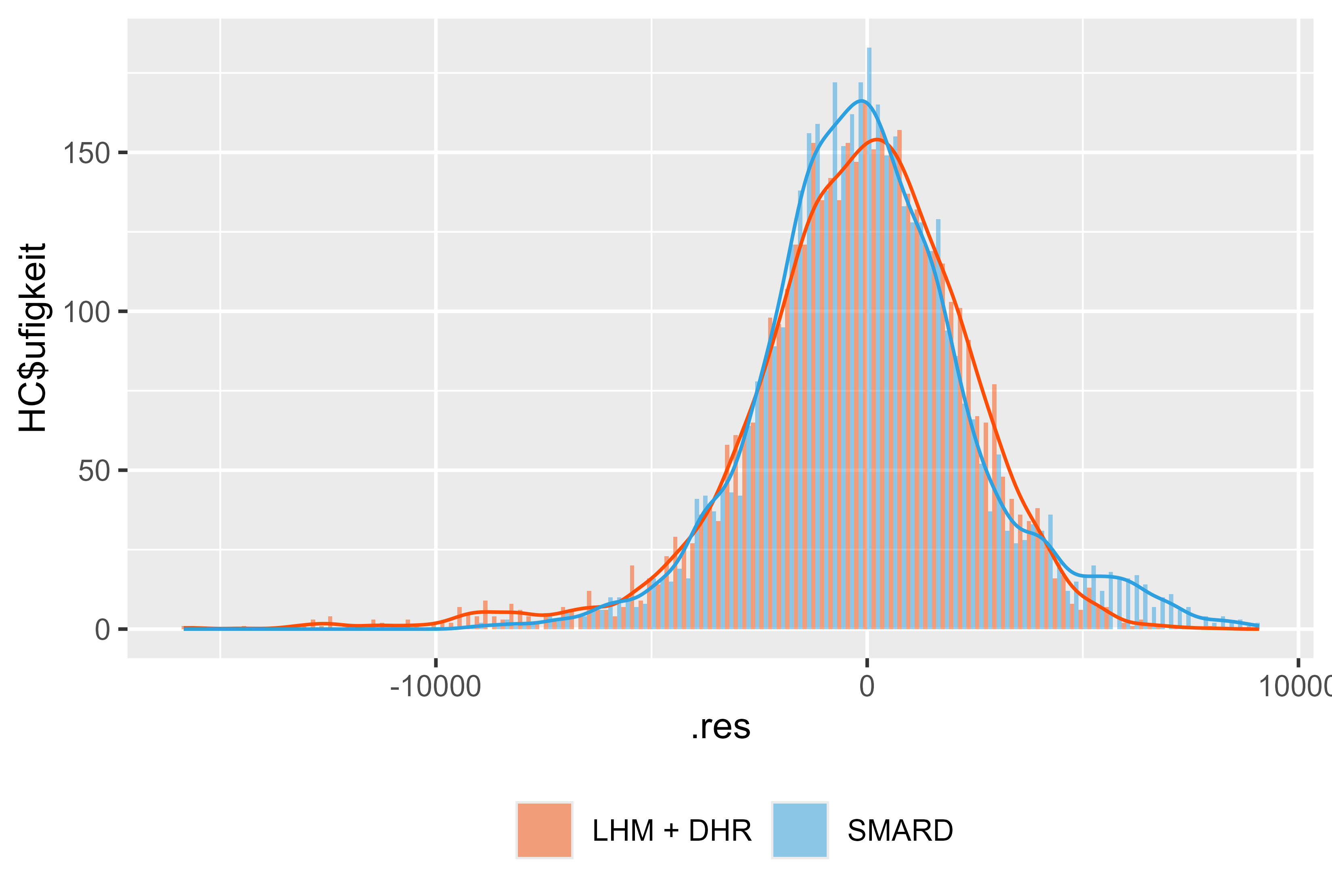그림 18 2024년 1월~7월의 잔차 LHM + DHR
| 색인 | 모델명 | RMSE | 마페 | 매 | 앙상블 |
|---|---|---|---|---|---|
| 2 | 실제 관찰 | 0.000 | 0.000000 | 0.000 | 진실 |
| 3 | 스마트 | 2480.693 | 3.602140 | 1869.466 | 거짓 |
| 4 | 스마트 | 2480.693 | 3.602140 | 1869.466 | 진실 |
| 5 | 버전_5 | 2626.807 | 3.816012 | 1937.670 | 진실 |
| 6 | 버전_0 | 2613.258 | 3.846888 | 1946.314 | 진실 |
| 7 | 버전_7 | 2770.359 | 4.107272 | 2076.045 | 진실 |
| 8 | 버전_8 | 2775.441 | 4.146788 | 2091.153 | 진실 |
| 9 | 버전_9 | 2887.179 | 4.177841 | 2100.381 | 진실 |
| 10 | 버전_6 | 2906.242 | 4.216517 | 2142.092 | 진실 |
| 11 | arima_14_2021_2023.rds | 3208.735 | 4.389492 | 2207.395 | 거짓 |
| 12 | arima_18_2021_2023.rds | 3208.735 | 4.389492 | 2207.395 | 거짓 |
| 13 | 버전_4 | 2875.929 | 4.535388 | 2255.645 | 진실 |
| 14 | 버전_2 | 2905.990 | 4.580770 | 2279.624 | 진실 |
| 15 | arima_9_2021_2023.rds | 3267.160 | 4.611857 | 2302.918 | 거짓 |
| 16 | arima_2_2021_2023.rds | 3251.390 | 4.614028 | 2301.447 | 거짓 |
| 17 | arima_4_2021_2023.rds | 3251.390 | 4.614028 | 2301.447 | 거짓 |
| 18 | arima_5_2021_2023.rds | 3251.390 | 4.614028 | 2301.447 | 거짓 |
| 19 | arima_13_2021_2023.rds | 3283.745 | 4.619636 | 2307.415 | 거짓 |
| 20 | arima_10_2021_2023.rds | 3265.913 | 4.625508 | 2314.395 | 거짓 |
| 21 | arima_0_2021_2023.rds | 3269.009 | 4.645944 | 2317.138 | 거짓 |
| 22 | arima_17_2021_2023.rds | 3269.009 | 4.645944 | 2317.138 | 거짓 |
| 23 | arima_16_2021_2023.rds | 3298.902 | 4.673116 | 2334.857 | 거짓 |
| 24 | arima_1_2021_2023.rds | 3312.429 | 4.696342 | 2340.193 | 거짓 |
| 24 | Prophet_0_2021_2023.rds | 3044.849 | 4.711527 | 2435.572 | 거짓 |
| 25 | arima_8_2021_2023.rds | 3332.217 | 4.716612 | 2358.085 | 거짓 |
| 26 | arima_11_2021_2023.rds | 3358.020 | 4.758970 | 2388.791 | 거짓 |
| 27 | arima_12_2021_2023.rds | 3430.191 | 5.022772 | 2495.067 | 거짓 |
| 28 | arima_7_2021_2023.rds | 3475.671 | 5.049287 | 2510.903 | 거짓 |
| 29 | 버전_3 | 3546.729 | 5.064654 | 2570.530 | 진실 |
| 30 | arima_15_2021_2023.rds | 3734.584 | 5.165147 | 2606.661 | 거짓 |
| 31 | arima_6_2021_2023.rds | 3748.583 | 5.375326 | 2723.837 | 거짓 |
| 32 | 버전_1 | 4495.568 | 6.483477 | 3229.647 | 진실 |
| 33 | arima_3_2021_2023.rds | 4558.982 | 6.953247 | 3453.387 | 거짓 |
| 34 | tslm_0_2021_2023.rds | 6760.994 | 11.189119 | 5694.949 | 거짓 |
| 35 | 평균_2021_2023.rds | 9489.303 | 16.406032 | 8101.476 | 거짓 |
| 36 | naive_2021_2023.rds | 14699.338 | 20.797370 | 12130.587 | 거짓 |
| 37 | Drift_2021_2023.rds | 14763.692 | 20.917883 | 12200.002 | 거짓 |
메모:
example/ensemble_model_2022_forecast 또는 example/ensemble_model_2023_forecast를 확인하세요.
다음과 같은 요소를 더 포함할 수 있습니다.
