강화 학습을 통해 하노이 탑 퍼즐을 해결합니다.
Numpy와 Pandas가 설치된 Python 환경에서 hanoi.py 스크립트를 실행하여 결과 섹션에 표시된 세 가지 플롯을 생성합니다. 예를 들어, 스크립트는 다른 수의 디스크 N 사용하여 게임을 플레이하도록 쉽게 조정할 수 있습니다.
강화 학습은 최근 Google Deepmind의 AlphaGo가 전문 인간 바둑 선수를 꺾으면서 새로운 관심을 받았습니다. 여기서는 더 간단한 퍼즐이 풀립니다: 하노이 타워 게임. 구현은 원래 Watkins & Dayan [1]이 제안한 Q-learning 알고리즘을 따릅니다.
하노이 타워 게임은 3개의 말뚝과 그 위로 미끄러질 수 있는 다양한 크기의 디스크로 구성됩니다. 퍼즐은 첫 번째 말뚝에 모든 디스크를 오름차순으로 쌓는 것으로 시작합니다. 가장 큰 디스크가 아래쪽에, 가장 작은 디스크가 위쪽에 있습니다. 게임의 목적은 모든 디스크를 세 번째 말뚝으로 옮기는 것입니다. 유일한 합법적인 이동은 맨 위에 있는 디스크를 한 페그에서 다른 페그로 가져가는 것이며, 디스크가 더 작은 디스크 위에 놓일 수 없다는 제한이 있습니다. 그림 1은 4개 디스크에 대한 최적의 솔루션을 보여줍니다.

그림 1. 4개 디스크에 대한 하노이 타워 퍼즐의 애니메이션 솔루션. (출처: 위키피디아).
Anderson [2]에 따르면 게임 상태를 튜플로 표현합니다. 여기서 i 번째 요소는 i 번째 디스크가 어느 페그에 있는지 나타냅니다. 디스크에는 크기가 커지는 순서대로 레이블이 지정되어 있습니다. 따라서 초기 상태는 (111)이고 원하는 최종 상태는 (333)입니다(그림 2).
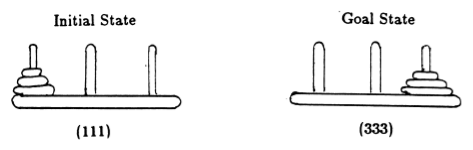
그림 2. 3개의 디스크로 구성된 하노이 탑 퍼즐의 초기 및 목표 상태. ([2]에서).
퍼즐의 상태와 적법한 움직임에 해당하는 상태 사이의 전환은 그림 3에 표시된 퍼즐의 상태 전환 그래프를 형성합니다.
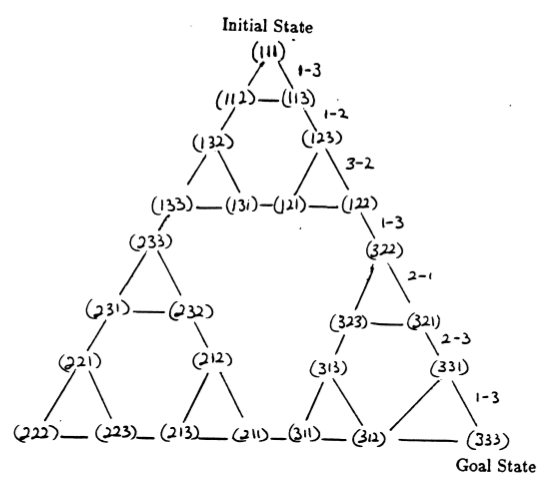
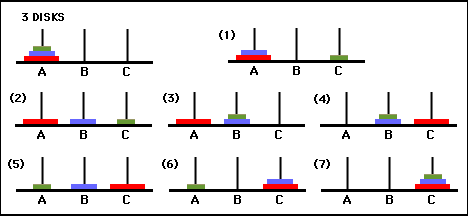
그림 3. 3개 디스크로 구성된 하노이 타워 퍼즐(위)과 해당 최적의 7개 이동 솔루션(아래)에 대한 상태 전이 그래프는 그래프의 오른쪽 경로를 따릅니다. ([2] 및 Mathforum.org에서).
하노이 탑 퍼즐을 푸는 데 필요한 최소 이동 횟수는 2 N - 1입니다. 여기서 N 은 디스크 수입니다. 따라서 N = 3인 경우 그림 3과 같이 7개의 동작으로 퍼즐을 풀 수 있습니다. 다음 섹션에서는 Q-학습을 통해 이것이 어떻게 달성되는지 간략하게 설명합니다.
R 과 '행동 가치' 행렬 Q 프로그램의 첫 번째 단계는 게임의 규칙을 포착하고 승리에 대한 보상을 제공하는 보상 매트릭스 R 을 생성하는 것입니다. 단순화를 위해 그림 4에는 N = 2 디스크에 대한 보상 매트릭스가 표시됩니다.
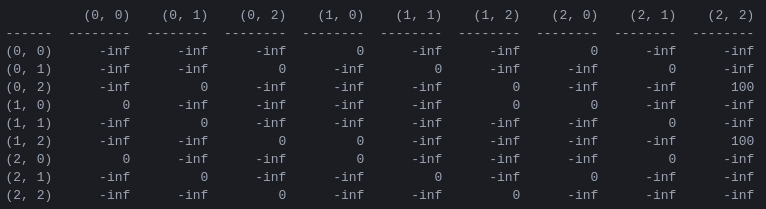
그림 4. N = 2 디스크가 있는 하노이 타워 퍼즐에 대한 보상 행렬 R ( i , j )번째 요소는 상태 i 에서 j 로 이동하는 데 대한 보상을 나타냅니다. 상태는 그림 2와 3에서와 같이 튜플로 레이블이 지정되어 있지만 페그는 1에서 3이 아닌 0에서 2로 '파이썬식으로' 색인이 지정된다는 차이점이 있습니다. 목표 상태(2,2)로 이어지는 이동에는 보상이 할당됩니다. 의 100, 불법적인 이동은 , 기타 모든 이동은 0입니다.
보상 매트릭스 R 즉각적인 보상만을 설명합니다. 100의 보상은 두 번째 상태 (0,2) 및 (1,2)에서만 달성될 수 있습니다. 다른 상태에서는 2개 또는 3개의 가능한 이동 각각의 보상이 0이며, 하나를 선택해야 할 뚜렷한 이유가 없습니다.
궁극적으로 우리는 각 상태에서 가능한 각 움직임에 '값'을 할당하여 이러한 값을 최대화함으로써 최적의 솔루션으로 이어지는 정책을 정의할 수 있습니다. 각 상태의 각 동작에 대한 '값' 행렬을 Q 라고 하며 Watkins & Dayan[1]이 설명한 대로 확률론적 방식으로 반복적으로 해결되거나 '학습'될 수 있습니다. 2개의 디스크에 대한 결과는 그림 5에 나와 있습니다.
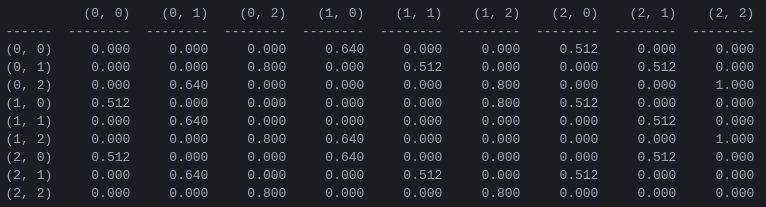
그림 5. 2개의 디스크가 있는 하노이 타워 게임에 대한 '작업 값' 행렬 Q , 할인 계수 = 0.8, 학습 계수 = 1.0, 1000개의 훈련 에피소드로 학습되었습니다.
행렬 Q 의 값은 본질적으로 그림 3의 상태 전이 그래프의 꼭지점에 할당될 수 있는 가중치이며, 에이전트를 초기 상태에서 목표 상태로 가장 짧은 방법으로 안내합니다. 이 예에서 상태 (0,0)에서 시작하여 Q 값이 가장 높은 이동을 연속적으로 선택함으로써 독자는 Q 매트릭스가 상태 (0,0) - (1의 시퀀스를 통해 에이전트를 유도한다는 것을 스스로 확신할 수 있습니다. ,0) - (1,2) - (2,2)는 2-디스크 타워 오브 하노이 게임의 3이동 최적 솔루션에 해당합니다(그림 6).
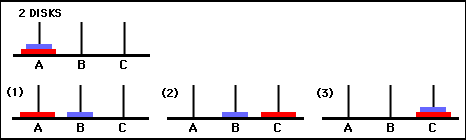
그림 6. 디스크 2개를 사용한 하노이 타워 게임의 솔루션. 연속된 상태는 각각 (0,0), (1,0), (1,2), (2,2)로 표시됩니다. (출처: mathforum.org).
행렬 Q 최적의 값으로 수렴된 이 예에서는 고정 정책을 정의합니다. 각 행에는 고유한 최대값을 갖는 하나의 작업이 포함됩니다. 그러나 학습 과정에서는 서로 다른 작업이 동일한 Q 값을 가질 수 있습니다. (특히, 이는 Q 0의 행렬로 초기화될 때 훈련이 시작되는 경우입니다.) 다음 섹션에 제시된 시뮬레이션에서 이러한 상황은 다음 확률론적 정책에 의해 처리됩니다. 최대 Q 값이 여러 작업에서 공유되는 경우 이러한 작업 중 하나를 무작위로 선택합니다.
Q-learning 알고리즘의 성능은 하노이 탑 퍼즐을 풀기 위해 걸리는 평균 이동 횟수를 계산하여 측정할 수 있습니다. 이 숫자는 결국 최적 값인 2N - 1에 도달할 때까지 훈련 에피소드 수에 따라 감소합니다. 여기서 N 은 디스크 수입니다(그림 7에서 N = 2, 3, 4에 대해 설명됨).
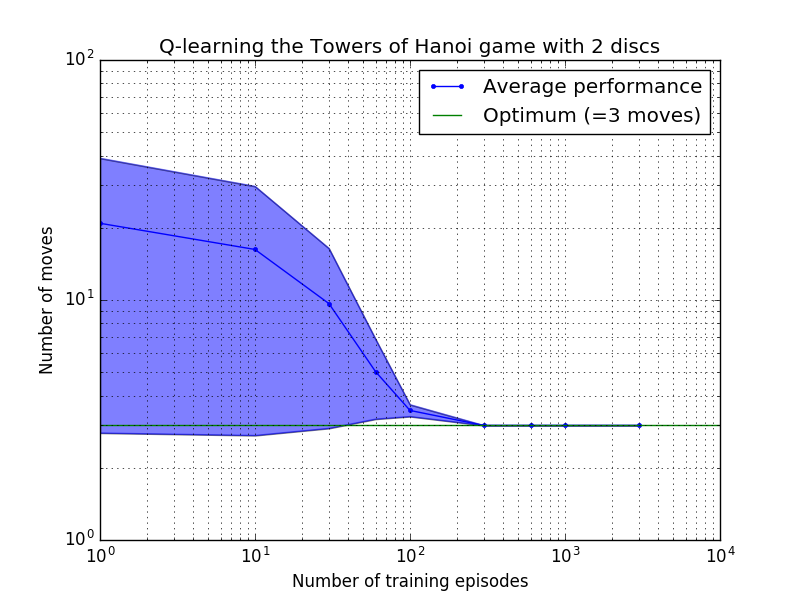
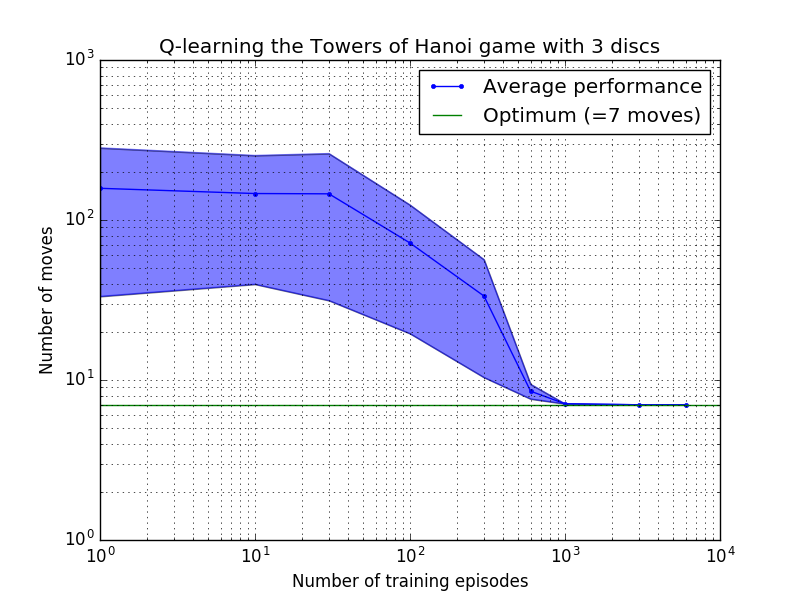
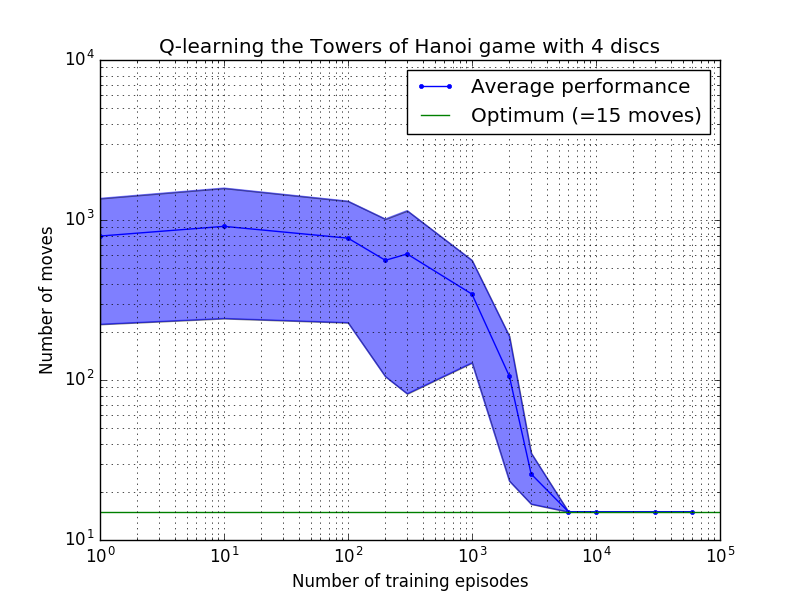
그림 7. 위에서 아래로 2, 3, 4개의 디스크를 사용한 하노이 타워 게임의 Q-학습 알고리즘 성능. 모든 경우에 학습은 할인 요인 = 0.8, 학습 요인 = 1.0으로 수행되었습니다. 파란색 실선은 각 결과 확률론적 정책에 대해 100번의 훈련과 100번의 게임 플레이에 대한 평균 성능을 나타냅니다. 음영 처리된 파란색 영역의 상한 및 하한은 추정된 표준 편차만큼 평균에서 오프셋됩니다. ( N = 3 및 N = 4의 경우 계산상의 제약으로 인해 훈련 에피소드 수와 플레이 시간이 각각 10회와 10회로 줄었습니다.)
그림 7의 학습 특성의 흥미로운 특징은 모든 경우에 초기 학습이 느리고 에이전트가 무작위로 이동을 선택하는 '제로 훈련' 정책보다 더 나은 성능을 발휘하지 못한다는 것입니다. 어느 시점에서 학습은 '변곡점'에 도달한 다음 가속된 속도로 최적의 이동 수로 수렴됩니다(이는 로그 척도에 의해 다소 과장되었지만).
Python 스크립트는 Q-러닝을 통해 디스크 수에 관계없이 최적으로 하노이 타워 퍼즐을 성공적으로 해결합니다. 스크립트는 다른 보상 매트릭스 R 사용하여 다른 문제에 쉽게 적용할 수 있습니다.
최적의 솔루션으로 수렴하는 데 필요한 교육 에피소드 수는 디스크 수 N 에 따라 크게 증가합니다. N=2 디스크의 경우 ~300에피소드가 소요되는 반면, N=4 의 경우 ~6,000이 소요됩니다. 학습 알고리즘의 가능한 개선은 Hengst [3]가 수행한 것처럼 자동으로 재귀 솔루션을 찾을 수 있도록 하는 것입니다.
[ 1 ] Watkins & Dayan, Q-learning , 기계 학습, 8, 279-292 (1992). (PDF).
[ 2 ] 앤더슨, 다층 연결주의 시스템을 통한 학습 및 문제 해결 , Ph.D. 논문 (1986). (PDF).
[ 3 ] Hengst, HEXQ를 사용한 강화 학습의 계층 구조 발견 , 기계 학습에 관한 제19차 국제 컨퍼런스 진행(2002). (PDF).