ai simplest network
1.0.0
이것은 가능한 가장 간단한 인공 신경망을 설명하고 시연한 것입니다.
인공신경망은 뇌에서 영감을 받아 인공신경망이 서로 연결되어 패턴을 저장하고 서로 소통하는 방식이다. 가장 단순한 형태의 인공 뉴런에는 하나 이상의 입력이 있습니다. 
각각은 특정한 무게를 가지고 있습니다 
그리고 하나의 출력 
.
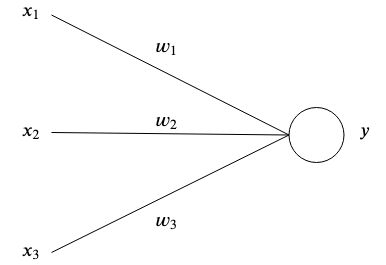
가장 단순한 수준에서 출력은 입력의 합과 가중치를 곱한 값입니다.
네트워크의 목적은 특정 출력을 학습하는 것입니다. 특정 입력이 주어지면 
매개변수가 많은 복잡한 함수를 근사화하여 
우리 스스로 생각해 낼 수 없다는 것입니다.
두 개의 입력이 있는 네트워크가 있다고 가정해 보겠습니다. 
그리고 
그리고 두 개의 가중치 
그리고 
.
주어진 입력이 원하는 출력을 생성하도록 가중치를 조정하는 것이 아이디어입니다.
가중치는 최적의 값을 미리 알 수 없기 때문에 일반적으로 무작위로 초기화되지만 단순화를 위해 둘 다 초기화합니다. 
.
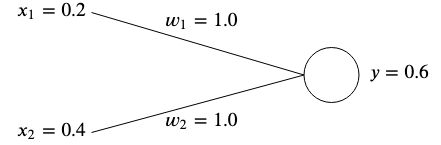
이 네트워크의 출력을 계산하면 다음과 같습니다.
출력되는 경우 예상 목표 값과 일치하지 않으면 오류가 발생합니다.
예를 들어 목표값을 얻고 싶다면 
그러면 우리는 다음과 같은 차이를 갖게 될 것입니다.
오류(비용 함수라고도 함)를 측정하는 일반적인 방법 중 하나는 평균 제곱 오류를 사용하는 것입니다.
입력과 목표 값의 연관성이 여러 개인 경우 오류는 각 연관성의 평균 합계가 됩니다.
평균 제곱 오차를 사용하여 결과가 원하는 목표에서 얼마나 멀리 떨어져 있는지 측정합니다. 제곱은 음수 부호를 제거하고 출력과 목표 간의 더 큰 차이에 더 많은 가중치를 부여합니다.
오류를 수정하려면 출력이 목표와 일치하도록 가중치를 조정해야 합니다. 우리 예에서는 ~에서 
에게 
트릭을 할 것입니다, 이후로
그러나 다양한 입력과 목표 값에 대해 신경망의 가중치를 조정하려면 이를 자동으로 수행하는 학습 알고리즘이 필요합니다.
아이디어는 오류를 사용하여 오류를 최소화하기 위해 각 가중치를 조정하는 방법을 이해하는 것이지만 먼저 기울기에 대해 배워야 합니다.
이는 본질적으로 함수의 가장 가파른 상승 방향을 가리키는 벡터입니다. 그라데이션은 다음과 같이 표시됩니다. 
이는 단순히 벡터로 표현된 함수의 각 변수의 편도함수입니다.
두 변수 함수의 경우 다음과 같습니다.
간단한 예를 통해 숫자를 입력하고 그래디언트를 계산해 보겠습니다. 함수가 있다고 가정해 보세요. 
, 그러면 그라데이션은 다음과 같습니다.
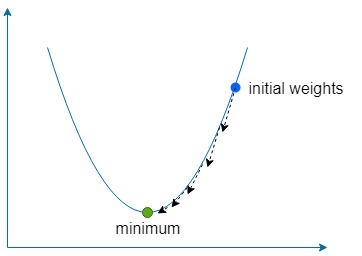
하강 부분은 단순히 그라디언트를 사용하여 함수의 가장 가파른 상승 방향을 찾은 다음 반대 방향으로 조금씩 여러 번 이동하여 함수 전역(또는 때로는 로컬) 최소값을 찾는 것을 의미합니다.
우리는 학습률(learning rate )이라는 상수를 사용합니다. 
그 방향으로 취해야 할 단계가 얼마나 작은지 정의합니다.
만약에 너무 크면 함수 최소값을 초과할 위험이 있지만, 너무 낮으면 네트워크를 학습하는 데 더 오랜 시간이 걸리고 얕은 로컬 최소값에 갇힐 위험이 있습니다.
우리의 두 가지 가중치에 대해 그리고 오류 함수에 대한 가중치의 기울기를 찾아야 합니다. 
둘 다 그리고 , 체인 규칙을 사용하여 그래디언트를 찾을 수 있습니다.
지금부터 표기하겠습니다. 
으로 
단순함을 뜻하는 용어.
그래디언트가 있으면 계산된 그래디언트에 학습률을 곱하여 가중치를 업데이트할 수 있습니다.
그리고 오류가 최소화되고 0에 가까워질 때까지 이 과정을 반복합니다.
포함된 예제는 경사하강법을 사용하여 두 개의 입력과 하나의 출력이 있는 신경망에 다음 데이터세트를 가르칩니다.
일단 학습되면 네트워크는 2가 주어지면 ~0을 출력해야 합니다. 와 ~ 주어졌을 때 그리고 
.
docker build -t simplest-network .
docker run --rm simplest-network
