
과 React의 Fiber 작업에 대해 알아야 하며, 다양한 Fiber 작업에는 우선 순위가 높은 작업을 먼저 처리해야 합니다. 예를 들어, 사용자의 클릭과 입력은 우선순위가 높은 작업입니다. 왜냐하면 사용자의 작업은 확실히 즉각적인 효과를 가져서 사용자 경험을 향상시키기를 원하기 때문입니다. 예를 들어 애니메이션 이벤트의 우선순위는 낮아야 합니다. 우선순위가 높은 새로운 작업이 대기열에 들어간 후 React는 이를 먼저 처리해야 합니다.
이러한 작업을 저장하기 위해 React에는 두 개의 작업 풀이 있습니다.
// 작업은 최소 힙에 저장됩니다. var taskQueue = []; var 타이머큐 = [];
taskQueue와 타이머큐는 모두 배열입니다. 전자는 즉시 실행될 작업을 저장하고 후자는 지연될 수 있는 작업을 저장합니다.
var newTask = {
id: taskIdCounter++, // 작업 ID 표시
callback, // 콜백 함수 PriorityLevel, // 작업 우선 순위 startTime, // 작업 시작 시간, 시점 만료Time, // 만료 시간, 시점 sortIndex: -1, // 작업 정렬, 값은 만료 시간에서 나오므로 값은 값 값이 작을수록 우선순위가 높아집니다.}; React에 새 작업이 들어오면 먼저 currentTime을 사용하여 현재 시간(performance.now() 또는 Date.now())을 기록합니다. 지연 매개변수이면 작업이 실행 시간을 시작합니다. startTime = currentTime + 지연;. 다음으로, startTime > currentTime이 설정되면 작업을 연기할 수 있음을 증명하고 해당 작업은 타이머큐에 들어가고, 그렇지 않으면 taskQueue에 들어갑니다.
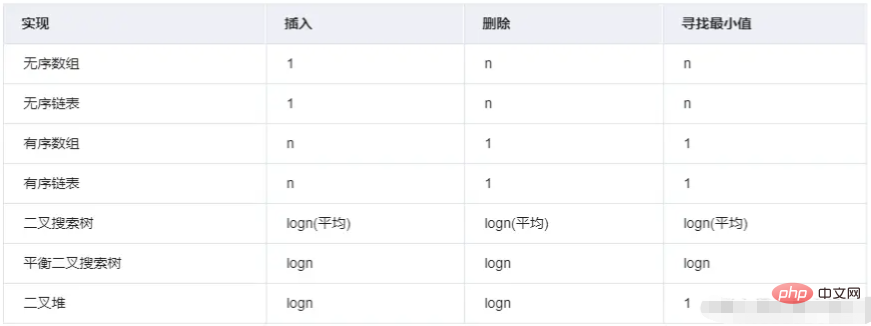
React는 어떻게 우선순위가 가장 높은 작업을 찾나요? taskQueue를 예로 들면, 동적 작업 풀(작업 대기열)이고 데이터 형식은 배열입니다. 물론 우선순위에 따라 정렬할 수도 있는데, 즉 Array.sort 처럼 새로운 작업이 큐에 추가되면 먼저 정렬한 뒤 우선순위가 가장 높은 작업을 찾아 실행한다. 그러나 Array.sort의 평균 시간 복잡도는 O(nlogn)이므로 최선의 해결책은 아닙니다.
SortIndex는 taskQueue의 newTask에서 정렬하는 데 사용됩니다. 이 값은 만료 시간에서 가져옵니다. 즉, 우선 순위가 높은 작업일수록 더 많이 이해하고 실행해야 하므로 만료 시간이 짧아집니다. 우선 순위가 높을수록 만료 시간이 짧을수록 sortIndex는 자연스럽게 작아집니다. 실제로 이것은 우선순위 큐입니다 .
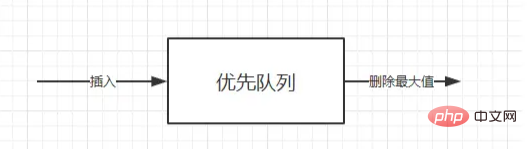
우선순위 큐는 큐의 일종이기도 합니다( 먼저 큐이고, 두 번째로 tail in, first out입니다 ). 유일한 차이점은 우선순위 큐의 큐에서 빼는 순서가 어떤 경우에는 우선순위에 따라 결정된다는 것입니다. , 요소 세트의 최소 또는 최대 요소는 우선순위 큐 ADT를 사용하여 작동할 수 있습니다. 우선순위 큐 ADT는 최소값 삽입 및 삭제 작업(최소 요소 반환 및 삭제)을 지원하는 데이터 구조입니다. 최대값 삭제 작업(최소 요소 반환 및 삭제)
가장 작은 키 값을 가진 요소의 우선순위가 가장 높은 경우 이 우선순위 큐를 오름차순 우선순위 큐라고 합니다(즉, 가장 작은 요소가 항상 먼저 삭제됩니다). 마찬가지로, 가장 큰 키 값을 가진 요소가 가장 높은 우선순위를 갖는 경우 이 유형의 우선순위 큐를 내림차순 우선순위 큐라고 합니다(즉, 가장 큰 요소가 항상 먼저 삭제됩니다). 이 두 유형은 대칭적이므로 사용자에게만 필요합니다. 오름차순 우선순위 큐와 같은 종류 중 하나에 집중합니다.
예를 들어 , 우리가 티켓을 구매할 때 우리는 모두 같은 우선순위로 줄을 섰고, 줄 앞에 있는 사람이 먼저 티켓을 구매했습니다. 그런데 군인이 와서 더 높은 우선순위를 갖고 바로 줄을 섰습니다. .
이 기능을 달성하기 위해 React에서는 최소 힙 (작은 루트 힙, 작은 상단 힙...)이 사용됩니다. 즉, taskQueue를 최소 힙으로 전환한 다음 실행을 위해 최상위 작업을 꺼내고 taskQueue를 힙하고 이를 최소 힙 데이터 구조로 유지하는 것입니다. taskQueue에 새 작업을 삽입할 때 힙도 있어야 하며 항상 최소 힙으로 유지해야 합니다.
: 어떤 곳에서는 힙을 우선순위 큐라고 합니다(정확하지 않음). 우선 큐이며 큐의 특성, 즉 " 선입선출 "을 갖습니다. . 둘째, 이 대기열의 요소에는 우선순위가 있으며, 우선순위가 높은 요소가 먼저 순위가 지정됩니다.
정확하게 말하면 힙은 우선순위 큐를 구현하는 방법입니다. 물론 우선순위 큐는 다른 방식으로도 구현될 수 있습니다.
이전에 힙 정렬이 불안정한 정렬이라고 말했지만 taskQueue는 이 프로세스가 안정적이기를 바랍니다. 즉, 두 작업의 만료 시간이 동일할 수 있다면 누가 입력하는지에 따라 다릅니다. 먼저 작업 풀은 newTask의 ID 값입니다. 새 작업이 올 때마다 ID가 1씩 증가합니다.
함수 비교(a, b) {
// 정렬 인덱스를 먼저 비교한 다음 작업 ID를 비교합니다.
const diff = a.sortIndex - b.sortIndex;
return diff !== 0 ? diff : a.id - b.id;
} 최소 힙을 이해하기 전에 기본 지식을 복습해 보겠습니다.
트리의 노드 차수가 2보다 크지 않은 정렬된 트리를 의미합니다. 가장 간단하고 중요한 트리입니다.
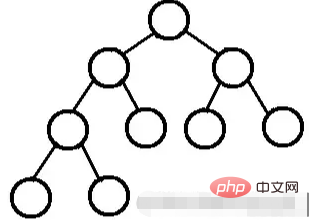
하위 노드가 없는 마지막 수준을 제외하고 각 수준의 모든 노드에 두 개의 하위 노드가 있는 이진 트리입니다.
그래픽 관점에서 볼 때 전체 이진 트리는 삼각형처럼 보입니다.
이진 트리의 수준 수가 K이고 총 노드 수가 (2^k) -1이면 완전 이진 트리입니다.
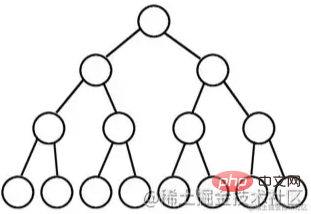
완전 이진 트리는 "딸은 양면을 갖는다"는 뜻으로 매우 완벽하므로 완전 이진 트리라고 부릅니다.
리프 노드를 제외한 모든 노드의 차수는 2입니다. 즉, 모든 노드의 차수는 0 또는 2만 될 수 있습니다.
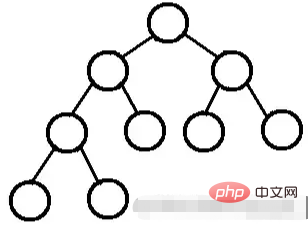
완벽한 이진 트리에는 자식이 없거나 두 자식이 모두 있습니다.
완전 이진 트리의 영어 원본 텍스트:
완전 이진 트리(FBT)는 리프를 제외한 모든 노드에 두 개의 자식이 있는 트리입니다.
완전 이진 트리의 원래 영어 텍스트는 다음과 같습니다.
완전 이진 트리(PBT)는 모든 리프 노드가 동일한 깊이에 있는 트리입니다. 모든 내부 노드는 차수 2를 가집니다.
모든 외국 서적은 완전 이진 트리와 완전 이진 트리에 관한 최초의 번역 교과서를 참조하지만 최초의 번역된 기사는 잘못 번역되었습니다. 이제 중국에서는 그들이 틀렸을 때만 실수를 할 수 있습니다(모든 사람이 틀리고 그러면 틀린 사람도 옳습니다. 예를 들어 로비스트...). 외국인 친구들과 이 두 가지 개념에 대해 이야기하고 싶다면 주목해야 할 부분이다.
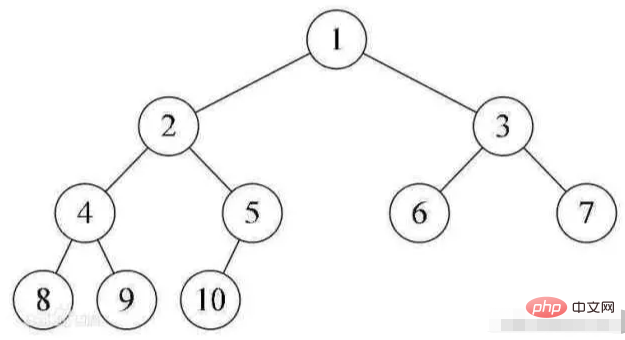
CBT(Binary Tree)는 마지막 레벨을 제외한 모든 레벨이 완전히 채워지고 모든 노드가 가능한 한 왼쪽
에 있는 이진 트리입니다. n개의 깊이 k 노드가 있는 이진 트리입니다. 위에서 아래로, 왼쪽에서 오른쪽으로 트리. i(1≤i≤n)라는 노드가 이진 트리에 있고 전체 이진 트리에서 노드 번호가 i인 경우 위치가 동일하면 이진 트리는 다음과 같습니다. 완전 이진 트리라고 합니다.
힙은 항상 다음 속성을 충족합니다.
먼저 큰 루트 힙을 이해해야 합니다
.작은 루트 힙 완전한 이진 트리에서는 모든 노드가 자식 노드보다 크거나 작으므로 여기에는 최대 힙과 최소 힙이라는 두 가지 상황이 있습니다.
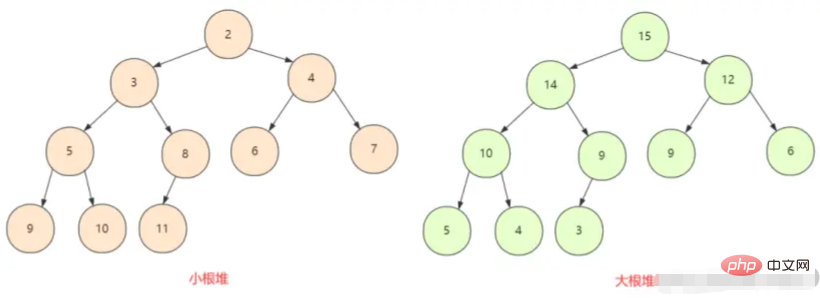
힙은 일반적으로 완전한 이진 트리 로 볼 수 있는 개체 배열입니다 . 물론 이진 트리는 배열로도 표현될 수 있습니다.
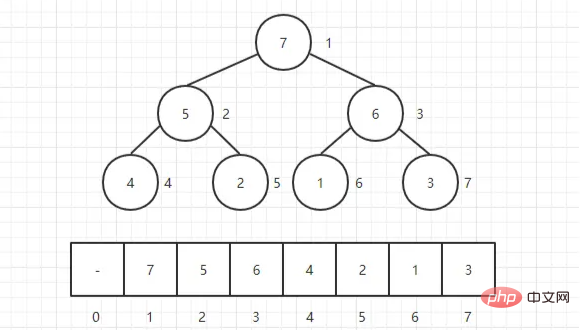
는 힙을 먼저 구축한 다음 조정하는 것입니다.
이진 트리(배열 표현)의 경우 "리프가 아닌 첫 번째 노드"부터 시작하여 아래에서 위로 조정하고 조정 규칙은 다음과 같습니다.
힙 구축은 O(n)입니다
.) 시간복잡도 과정.
① 리프가 아닌 첫 번째 노드부터 시작하여 스왑 다운(shiftDown)을 판단하여 현재 노드와 자식이 힙 속성을 유지할 수 있도록 합니다.
② 그러나 교환이 힙 구조 속성을 깨뜨릴 경우 일반적인 노드 교체는 문제가 되지 않을 수 있습니다. 그런 다음 중지될 때까지 교체된 노드를 다시 ShiftDown해야 합니다.
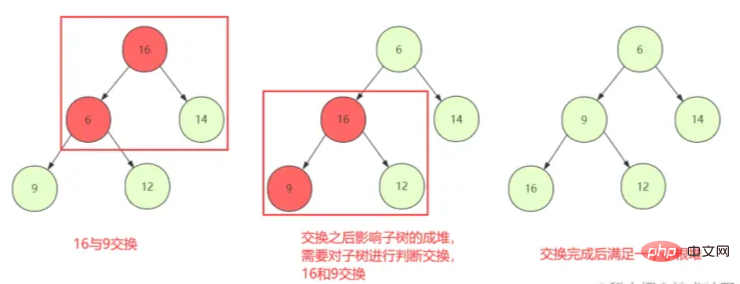
힙
구조를 조정한힙 구조가 파괴될 수 있습니다.
① 그러니 간단히 마지막 요소를 먼저 넣으세요. 이런 식으로 스왑 시프트(shiftDown)만 판단하면 되지만, 이때 힙 전체의 크기가 변경되었다는 점에 유의해야 합니다. 우리는 버린 위치를 논리적으로 사용하지 않을 것이므로 힙을 포함시켜야 합니다. 함수를 설계할 때 크기 매개변수.
② 힙의 모든 요소를 얻을 때까지 위의 작업을 반복합니다.
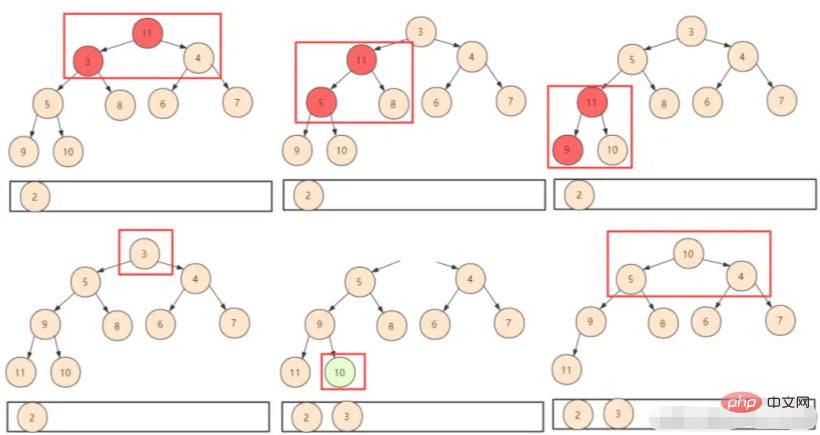
힙 알고리즘의 복잡도 분석을 보면, 기존의 힙 생성 시간 복잡도는 O(n)이었다. 힙의 상단이 삭제된 다음 아래쪽으로 교체될 때마다 각 항목의 수가 기록됩니다. 이렇게 하면 복잡도는 O(nlogn)이 되고, 전체 시간 복잡도는 O(n)+O(nlogn)=O(nlogn)이 됩니다.
힙은 컬렉션의 최대 가치를 유지하는 데 적합합니다.
요소가 힙에서 튀어나온 후 힙의 최상위 요소(즉, 두 번째로 높은 값)를 얻기 위해 다시 조정하는 비용은 상대적으로 낮습니다. -완제품이고, 두 번째로 높은 값은 반제품에서 구함. 물론 비용도 상대적으로 낮고, 시간복잡도도 O(logn)이지만, 두 번째로 높은 값을 찾기 위해 한 번 순회하면, 시간 복잡도는 O(n)입니다.
코드는 Javascript ES6으로 작성되었습니다.
클래스 힙 {
생성자(데이터, 구성 요소) {
this.data = 데이터 ? 데이터 : [];
// 비교 규칙: 보다 유연하게 값이나 객체를 비교할 수 있습니다. this.compartor = comp ? comp : (ab) => ab;
// 힙에 맞게 조정(우선순위 큐)
this.heapify();
}
힙파이() {
if(this.size() <= 1) return;
// 리프가 아닌 첫 번째 노드에서 조정을 시작하거나 마지막 요소에서 조정할 수 있습니다. for(let i=Math.floor((this.size()-2)/2); i>=0; i-- ) {
//힙 조정. 하향 조정은 재귀를 사용하여 구현할 수도 있습니다. 여기서는 반복을 사용하여 this.shiftDown(i)을 구현합니다.
}
}
// 하향 조정 ShiftDown(i) {
왼쪽 = 2*i +1;
오른쪽 = 2*i +2;
len = this.size();
동안(i < len) {
findIndex = i를 두십시오;
//왼쪽 자식이 "더 크다"
if(왼쪽 < len && this.compartor(this.data[왼쪽], this.data[findIndex]) < 0) {
findIndex = 왼쪽;
}
// 오른쪽 자식은 "더 크다"
if(right < len && this.compartor(this.data[right], this.data[findIndex]) < 0) {
findIndex = 오른쪽;
}
if(i !== findIndex) {
//현재 노드를 더 큰 값으로 교환 [this.data[i], this.data[findIndex]] = [this.data[findIndex], this.data[i]];
// 이 레이어를 조정한 후 하위 레이어의 힙 특성에 영향을 줄 수 있으므로 계속해서 하위 레이어를 조정한다(반복구현 또는 재귀)
i = 찾기인덱스;
왼쪽 = 2*i +1;
오른쪽 = 2*i +2;
}
또 다른 {
// 조정이 필요하지 않으면 점프 아웃합니다(반드시 점프 아웃해야 합니다. 그렇지 않으면 루프가 종료될 수 없습니다).
부서지다;
}
}
}
// 상향 조정shiftUp(i){
// 부모의 첨자를 찾습니다. let parentIndex = Math.floor((i-1)/2);
// 최대값을 0으로 조정
while(parentIndex >=0 ) {
findIndex = i를 두십시오;
if(this.compartor(this.data[parentIndex], this.data[findIndex]) > 0) {
findIndex = 부모 인덱스;
}
if(findIndex !== i) {
[this.data[i], this.data[findIndex]] = [this.data[findIndex], this.data[i]];
i = 찾기인덱스;
parentIndex = Math.floor((i-1)/2);
}
또 다른 {
부서지다;
}
}
}
// 힙에 있는 모든 요소의 수를 가져옵니다. size(){
this.data.length를 반환합니다.
}
// 힙의 첫 번째 요소를 가져옵니다. peek(){
if(!this.size())는 null을 반환합니다.
this.data[0]을 반환합니다.
}
//힙에 요소 추가 push(x){
this.data.push(x);
this.shiftUp(this.data.length-1);
}
// 힙에서 첫 번째 요소를 팝합니다. pop(){
if(!this.size())는 null을 반환합니다.
res = this.data[0];
if(this.size() == 1) {
this.data.pop();
}
또 다른 {
this.data[0] = this.data[this.data.length-1];
this.data.length = this.data.length-1;
this.shiftDown(0);
}
해상도를 반환;
}
} 하자 arr = [2,9,8,6,3,10,5,7,4,1];
comp = (a, b) => ab라고 놔두세요;
heap = new Heap(arr, comp);
res = [];
while(heap.size()) {
res.push(heap.pop());
}
console.log(res); arr의 요소는 객체일 수도 있습니다.
React 소스코드의 packages/scheduler 디렉토리는 React의 작업 스케줄링 모듈과 관련된 코드입니다.
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src/Scheduler.js
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src /SchedulerMinHeap.js
/**
* 저작권 (c) Facebook, Inc. 및 그 계열사.
*
* 이 소스 코드는 MIT 라이선스에 따라 라이선스가 부여됩니다.
* 이 소스 트리의 루트 디렉터리에 LICENSE 파일이 있습니다.
*
* @flow 엄격함
*/
유형 힙 = Array<노드>;
유형 노드 = {|
아이디: 번호,
sortIndex: 숫자,
|};
내보내기 함수 push(heap: Heap, node: Node): void {
const 인덱스 = 힙 길이;
힙.푸시(노드);
siftUp(힙, 노드, 인덱스);
}
내보내기 함수 peek(heap: Heap): Node null {
const 먼저 = 힙[0];
첫 번째 반환 === 정의되지 않음 ? null : 첫 번째;
}
내보내기 함수 pop(힙: 힙): 노드 null {
const 먼저 = 힙[0];
if (첫 번째 !== 정의되지 않음) {
const last = heap.pop();
if (마지막 !== 처음) {
힙[0] = 마지막;
siftDown(힙, 마지막, 0);
}
먼저 돌아가세요.
} 또 다른 {
null을 반환;
}
}
함수 siftUp(힙, 노드, i) {
인덱스 = i로 두십시오;
동안 (참) {
const parentIndex = (색인 - 1) >>> 1;
const 부모 = 힙[parentIndex];
if (부모 !== 정의되지 않음 && 비교(부모, 노드) > 0) {
// 상위 위치가 더 큽니다.
힙[parentIndex] = 노드;
힙[인덱스] = 부모;
인덱스 = 부모 인덱스;
} 또 다른 {
// 부모가 더 작습니다.
반품;
}
}
}
함수 siftDown(힙, 노드, i) {
인덱스 = i로 두십시오;
const 길이 = 힙 길이;
while (인덱스 < 길이) {
const leftIndex = (색인 + 1) * 2 - 1;
const 왼쪽 = 힙[leftIndex];
const rightIndex = leftIndex + 1;
const 오른쪽 = 힙[rightIndex];
// 왼쪽 또는 오른쪽 노드가 더 작으면 그 중 더 작은 노드로 바꿉니다.
if (왼쪽 !== 정의되지 않음 && 비교(왼쪽, 노드) < 0) {
if (오른쪽 !== 정의되지 않음 && 비교(오른쪽, 왼쪽) < 0) {
힙[인덱스] = 오른쪽;
힙[rightIndex] = 노드;
인덱스 = 오른쪽 인덱스;
} 또 다른 {
힙[인덱스] = 왼쪽;
힙[leftIndex] = 노드;
인덱스 = leftIndex;
}
} else if (오른쪽 !== 정의되지 않음 && 비교(오른쪽, 노드) < 0) {
힙[인덱스] = 오른쪽;
힙[rightIndex] = 노드;
인덱스 = 오른쪽 인덱스;
} 또 다른 {
// 어느 자식도 더 작지 않습니다.
반품;
}
}
}
함수 비교(a, b) {
// 정렬 인덱스를 먼저 비교한 다음 작업 ID를 비교합니다.
const diff = a.sortIndex - b.sortIndex;
return diff !== 0 ? diff : a.id - b.id;
} 우리가 구현한 최소 힙은 React의 구현과 약간 다르지만 아이디어는 동일하며 코드만 다르게 작성되었습니다.
React의 작업 스케줄링은 최소 힙을 사용하여 구현됩니다. 이전에 최소 힙에 대해 어느 정도 이해했다면 이 내용을 더 빨리 배울 것입니다. 개인적으로는 초기에 지식을 축적하는 것이 얼마나 중요한지 생각하는데, 이 과정이 지루할 수도 있습니다. 이 시점에서 당신은 어떤 알고리즘을 알고 있다고 생각합니까? 사실 이러한 알고리즘은 초보자 수준이며 아직 시작하지도 않았습니다. React의 작업 스케줄링 시나리오에서는 구현해야 할 요구 사항이 매우 명확하고 사용할 데이터 구조와 알고리즘도 명확하기 때문입니다. 일부 실제 시나리오에서는 특정 요구 사항을 알고 있지만 어떤 데이터 결과와 알고리즘을 사용해야 할지 알 수 없습니다. 요구 사항을 추상화하고 추상 데이터 모델을 기반으로 특정 데이터 구조와 알고리즘을 설계해야 합니다. .