MLE com distribuições normais - Laboratório

Introdução

Neste laboratório, colocaremos em prática as fórmulas matemáticas que vimos na lição anterior para ver como o MLE funciona com distribuições normais.

Objetivos

Você será capaz de:

Compreenda e descreva como o MLE funciona com distribuições normais
Ajustar uma distribuição normal a determinados dados identificando média e variância
Compare visualmente a distribuição ajustada com a distribuição real

Nota: *Uma derivação detalhada de todas as equações MLE com provas pode ser vista neste site. *

MLE em Python

Vamos ver um exemplo de MLE e ajustes de distribuição com Python abaixo. Aqui, scipy.stats.norm.fit calcula os parâmetros de distribuição usando a estimativa de máxima verossimilhança.

Importe as bibliotecas necessárias

 from scipy . stats import norm # for generating sample data and fitting distributions
import matplotlib . pyplot as plt
plt . style . use ( 'seaborn' )
import numpy as np

Gere uma matriz de 200 amostras aleatórias de uma dist normal com média 0 e stdv 1

 sample = None

Ajuste de distribuição através de MLE

- Use `stats.norm.fit(data)` para ajustar uma distribuição aos dados acima.

- Isso retorna uma lista de dois parâmetros: (média,: parâmetros[0] e std: parâmetros[1]) por meio de uma abordagem MLE

 param = None

#param[0], param[1]
# (0.08241224761452863, 1.002987490235812)

Calcule o PDF a partir de a) parâmetros de dados reais b) parâmetros ajustados com `x = np.linspace(-5,5,100)`

 x = np . linspace ( - 5 , 5 , 100 )

# Generate the pdf from fitted parameters (fitted distribution)
fitted_pdf = None
# Generate the pdf without fitting (normal distribution non fitted)
normal_pdf = None

Visualize ambos os PDFs

 # Your code here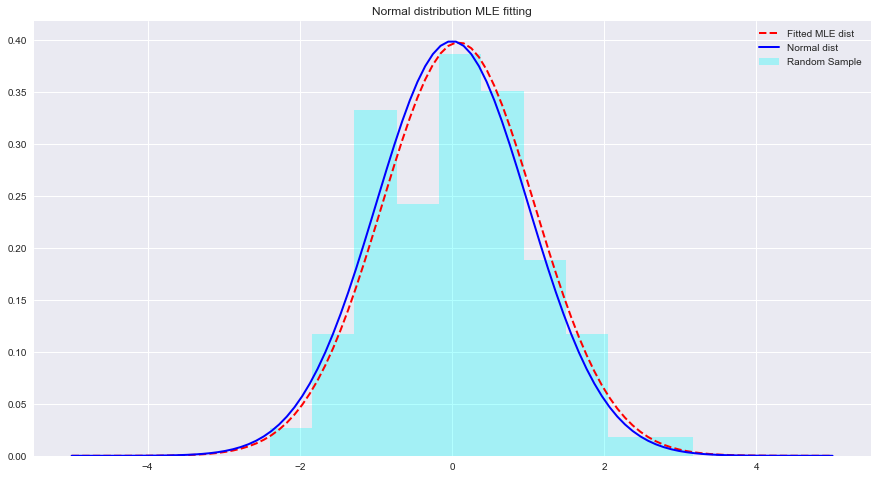

png

 #  Your comments/observations

Resumo

Neste breve laboratório, analisamos a configuração bayesiana em um contexto gaussiano, ou seja, quando as variáveis aleatórias subjacentes são normalmente distribuídas. Aprendemos que o MLE pode estimar os parâmetros desconhecidos de uma distribuição normal, maximizando a probabilidade da média esperada. A média esperada aproxima-se muito da média de uma distribuição normal não ajustada dentro desse espaço de parâmetros. Avançaremos com esse entendimento para aprender como tais estimativas são realizadas na estimativa das médias de uma série de classes presentes na distribuição de dados usando o Classificador Naive Bayes.

Expandir

Informações adicionais