Inverter Matrix usando uma rede neural.
As matrizes invertidas apresentam desafios exclusivos para as redes neurais, principalmente devido a limitações inerentes ao executar operações aritméticas precisas, como multiplicação e divisão em ativações. As redes densas tradicionais geralmente precisam de ajuda com essas tarefas, pois não são projetadas explicitamente para lidar com as complexidades envolvidas na inversão da matriz. Experimentos realizados com redes neurais densas simples mostraram dificuldades significativas para alcançar inversões de matriz precisas. Apesar de várias tentativas de otimizar o processo de arquitetura e treinamento, os resultados geralmente precisam de melhorias. No entanto, a transição para uma arquitetura mais complexa-uma rede residual de 7 camadas (Resnet)-pode levar a melhorias acentuadas no desempenho.
A arquitetura Resnet, conhecida por sua capacidade de aprender representações profundas por meio de conexões residuais, se mostrou eficaz no combate à inversão da matriz. Com milhões de parâmetros, essa rede pode capturar padrões complexos nos dados que os modelos mais simples não podem. No entanto, essa complexidade tem um custo: dados substanciais de treinamento são necessários para a generalização eficaz.
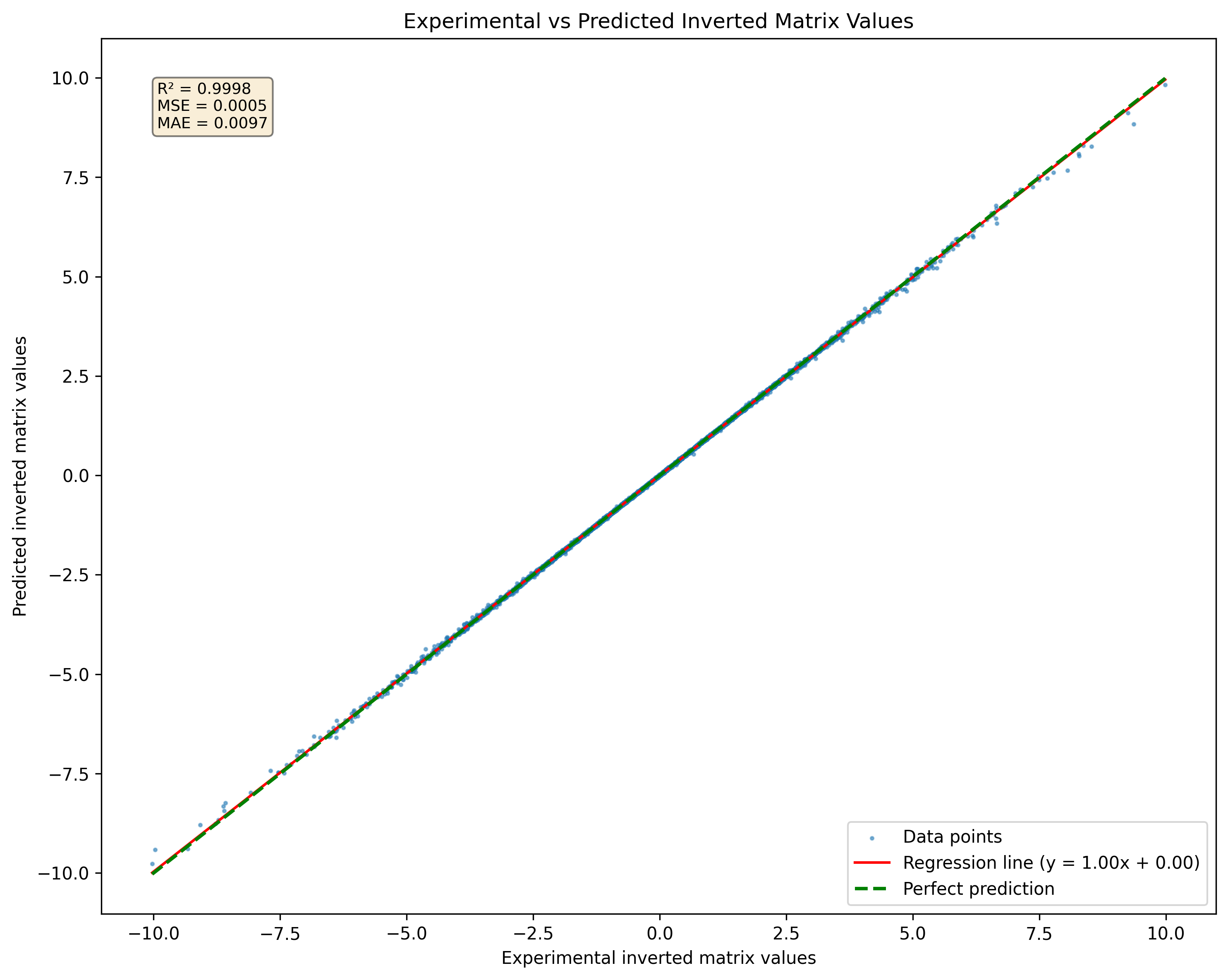Figura 1: Visualização de uma rede neural prevista Matriz invertida para um conjunto de matrizes 3x3 nunca visto no conjunto de dados
Para avaliar o desempenho da rede neural na previsão de inversões da matriz, é empregada uma função de perda específica:
Nesta equação:
O objetivo é minimizar a diferença entre a matriz de identidade e o produto da matriz original e seu inverso previsto. Essa função de perda mede efetivamente o quão próximo o inverso previsto é de ser preciso.
Além disso, se
Essa função de perda oferece vantagens distintas sobre as funções de perda tradicional, como erro médio ao quadrado (MSE) ou erro absoluto médio (MAE).
Medição direta da precisão da inversão O objetivo principal da inversão da matriz é garantir que o produto de uma matriz e seu inverso gerem a matriz de identidade. A função de perda captura diretamente esse requisito medindo o desvio da matriz de identidade. Por outro lado, MSE e MAE se concentram nas diferenças entre os valores previstos e os valores verdadeiros sem abordar explicitamente a propriedade fundamental da inversão da matriz.
A ênfase na integridade estrutural usando uma função de perda que avalia a proximidade do produto AA -1AA -1, de II, enfatiza a manutenção da integridade estrutural das matrizes envolvidas. Isso é particularmente importante em aplicações em que preservar as relações lineares é crucial. Funções de perda tradicional como MSE e MAE não respondem por esse aspecto estrutural, potencialmente levando a soluções que minimizam o erro, mas não conseguem satisfazer os requisitos matemáticos da inversão da matriz.
Aplicabilidade a matrizes não singulares Essa função de perda assume inerentemente que as matrizes sendo invertidas são não singulares (ou seja, invertíveis). Em cenários em que as matrizes singulares estão presentes, as funções tradicionais de perda podem produzir resultados enganosos, pois não representam a impossibilidade de obter um inverso válido. A função de perda proposta destaca essa limitação produzindo erros maiores ao tentar inverter matrizes singulares.
Uma limitação significativa ao usar redes neurais para inversão da matriz é sua incapacidade de lidar com matrizes singulares de maneira eficaz. Uma matriz singular não tem um inverso; Assim, qualquer tentativa de uma rede neural de prever um inverso para tais matrizes produzirá resultados incorretos. Na prática, se uma matriz singular for apresentada durante o treinamento ou a inferência, a rede ainda poderá produzir um resultado, mas essa saída não será válida ou significativa. Essa limitação ressalta a importância de garantir que os dados de treinamento consistem em matrizes não singulares sempre que possível.
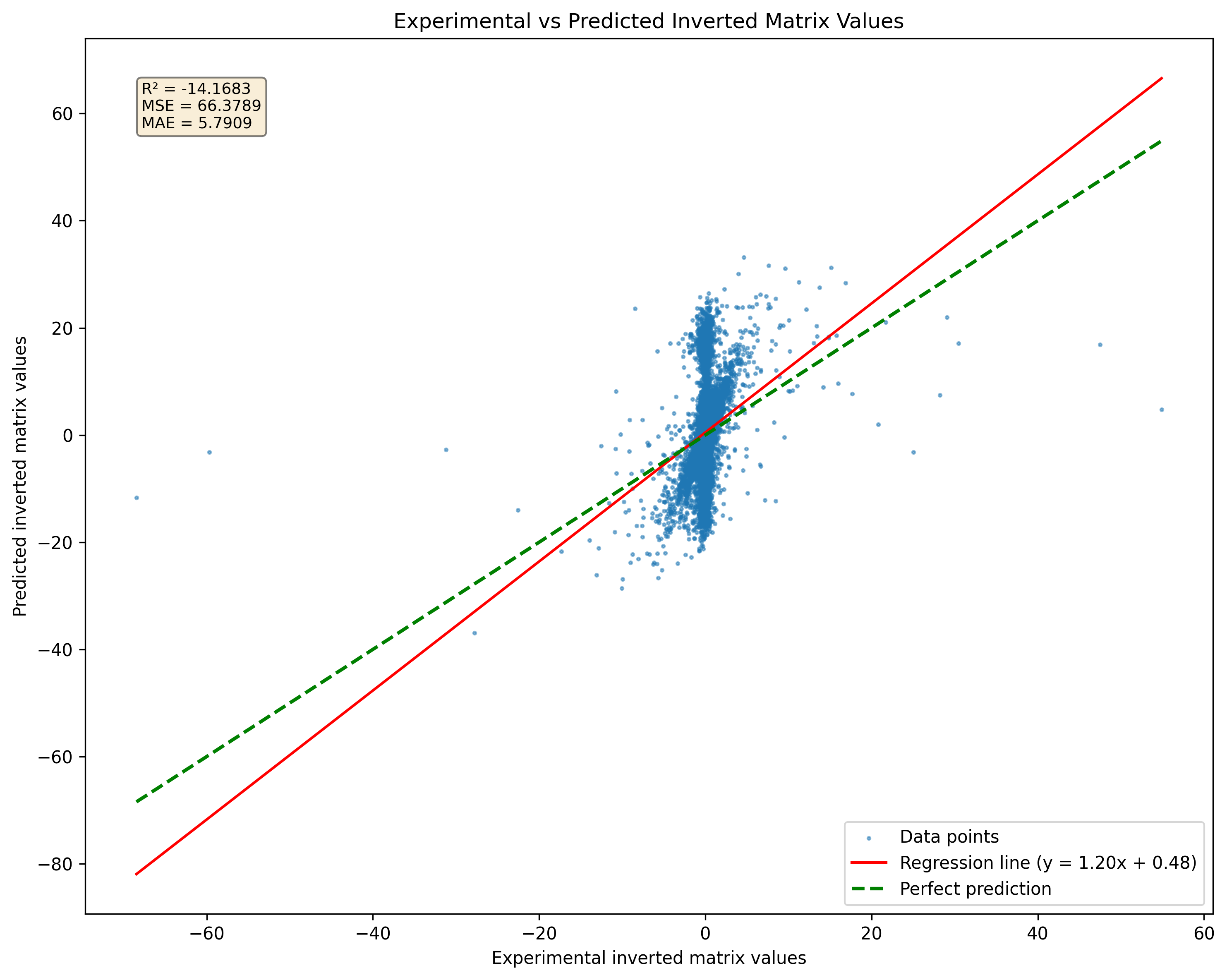Figura 2: Comparação da previsão do modelo para matrizes singulares versus pseudoinversões. Observe que o modelo produzirá resultados, independentemente da singularidade da matriz.
A pesquisa indica que um modelo de resnet pode memorizar uma boa quantidade de amostras sem perda significativa de precisão. No entanto, aumentar o tamanho do conjunto de dados para 10 milhões de amostras pode levar a um excesso de ajuste grave. Esse excesso de ajuste ocorre apesar do grande volume de dados, destacando que o aumento do tamanho do conjunto de dados não garante generalização melhorada para modelos complexos. Para enfrentar esse desafio, uma estratégia contínua de geração de dados pode ser adotada. Em vez de confiar em um conjunto de dados estático, as amostras podem ser geradas em tempo real e alimentadas à rede à medida que são criadas. Essa abordagem, que é crucial para mitigar o excesso de ajuste, não apenas fornece uma gama diversificada de exemplos de treinamento, mas também garante que o modelo seja exposto a um conjunto de dados em constante evolução.
Em resumo, embora a inversão da matriz seja inerentemente desafiadora para as redes neurais devido a limitações nas operações aritméticas, alavancar arquiteturas avançadas como a ResNet podem produzir melhores resultados. No entanto, deve ser considerada cuidadosa aos requisitos de dados e riscos excessivos. A geração de amostras de treinamento continuamente pode aprimorar o processo de aprendizado do modelo e melhorar o desempenho nas tarefas de inversão da matriz. Esta versão mantém um tom impessoal ao discutir os desafios e estratégias no treinamento de redes neurais para inversão da matriz.
DeepMatrixInversion é distribuído pela licença LGPLV3
Para saber mais em detalhes como os licenciadores funcionam, leia o arquivo "Licença" ou acesse "http://www.gnu.org/license/lgpl-3.0.html"
Atualmente, a DeepMatrixinversion é propriedade de Giuseppe Marco Randazzo.
Para instalar o Repositório DeepMatrixInversion, você pode escolher entre usar poesia, pip ou pipx abaixo estão as instruções para ambos os métodos.
git clone https://github.com/gmrandazzo/DeepMatrixInversion.git
cd DeepMatrixInversion
python3 -m venv .venv
. .venv/bin/activate
pip install poetry
poetry install
Isso configurará seu ambiente com todos os pacotes necessários para executar o DeepMatrixInversion.
Crie um ambiente virtual e instale DeppMatrixinVersion com PIP
python3 -m venv .venv
. .venv/bin/activate
pip install git+https://github.com/gmrandazzo/DeepMatrixInversion.git
Se você preferir usar o PIPX, que permite instalar aplicativos Python em ambientes isolados, siga estas etapas:
python3 -m pip install --user pipx
apt-get install pipx
brew install pipx
sudo dnf install pipx
PiPX Install git+https: //github.com/gmrandazzo/deepmatrixinversion.git
Para treinar um modelo que pode executar a inversão da matriz, você usará o comando dmxtrain. Este comando permite especificar vários parâmetros que controlam o processo de treinamento, como o tamanho das matrizes, o intervalo de valores e a duração do treinamento.
dmxtrain --msize < matrix_size > --rmin < min_value > --rmax < max_value > --epochs < number_of_epochs > --batch_size < size_of_batches > --n_repeats < number_of_repeats > --mout < output_model_path > dmxtrain --msize --rmin -1 --rmax 1 --epochs 5000 --batch_size 1024 --n_repeats 3 --mout ./Model_3x3
--msize <matrix_size>: Specifies the size of the square matrices to be generated for training. For example, 3 for 3x3 matrices.
--rmin <min_value>: Sets the minimum value for the random elements in the matrices. For instance, -1 will allow negative values.
--rmax <max_value>: Sets the maximum value for the random elements in the matrices. For example, 1 will limit values to a maximum of 1.
--epochs <number_of_epochs>: Defines how many epochs (complete passes through the training dataset) to run during training. A higher number typically leads to better performance; in this case, 5000.
--batch_size <size_of_batches>: Determines how many samples are processed before the model is updated. A batch size of 1024 means that 1024 samples are used in each iteration.
--n_repeats <number_of_repeats>: Indicates how many times to repeat the training process with different random seeds or initializations. This can help ensure robustness; for instance, repeating 3 times.
--mout <output_model_path>: Specifies where to save the trained model. In this example, it saves to ./Model_3x3.
Depois de treinar seu modelo, você pode usá -lo para executar a inversão da matriz em novas matrizes de entrada. O comando para inferência é o DMXInvert, que pega uma matriz de entrada e produz seu inverso.
AVISO: O DMXInvert pode inverter uma matriz maior que a usada para treinar o modelo através da fórmula de inversão da matriz Sherman-Morrison-Woodbury. Esse recurso funciona apenas com matrizes cujo tamanho de bloco pode ser dividido pelo tamanho do bloco de treinamento do modelo sem lembrete. O recurso é altamente experimental e pode precisar ser revisado.
dmxinvert --inputmx <input_matrix_file> --inverseout <output_csv_file> --model <model_path>
dmxinvert --inputmx input_matrix.csv --inverseout output_inverse.csv --model ./Model_3x3_*
--inputmx <input_matrix_file>: Specifies the path to the input matrix file that you want to invert. This file should contain a valid matrix format (e.g., CSV).
--inverseout <output_csv_file>: Indicates where to save the resulting inverted matrix. The output will be saved in CSV format.
--model <model_path>: Provides the path to the trained model that will be used for performing the inversion.
Geração de um conjunto de dados artificial com matriz de entrada e saída invertida é feita dmx dmxdataSetGenerator
dmxdatasetgenerator 3 10 -1 1 test_3x3_range_-1+1
Isso gerará 10 matrizes de tamanho 3x3 com números em um intervalo de -1 a +1.
dmxdatasetgenerator [matrix size] [number of samples] [range min] [range max] [outname_prefix]
Em seguida, o conjunto de dados pode ser validado usando DMXDatasetVerify
dmxdatasetverify test_3x3_range_-1+1_matrices_3x3.mx test_3x3_range_-1+1_matrices_inverted_3x3.mx invertible
Dataset valid.
dmxdatasetverify [dataset matrix to invert] [dataset matrix inverted] [type: invertible or singular]
O arquivo de matriz de entrada deve ser formatado da seguinte forma:
0.24077047370124594,-0.5012474139608847,-0.5409542929032876
-0.6257864520097793,-0.030705148203584942,-0.13723920334288975
-0.48095686716222064,0.19220406568380666,-0.34750000491973854
END
0.4575368007107925,0.9627977617090073,-0.4115240560547333
0.5191433428806012,0.9391491187187144,-0.000952683255491138
-0.17757763984424968,-0.7696584771443977,-0.9619759413623306
END
-0.49823271153034154,0.31993947803488587,0.9380291202366384
0.443652116558352,0.16745965310481048,-0.267270356721347
0.7075720067281346,-0.3310912886946993,-0.12013367141105102
END
Cada bloco de números representa uma matriz separada seguida por um marcador final indicando o final dessa matriz.
