Solver de cubo de Rubik para cubos muito grandes.
Resolve qualquer cubo de qualquer tamanho de 1 a 65536. O código pode ser facilmente modificado para lidar com cubos ainda maiores. No entanto, a limitação primária é a quantidade de memória em um sistema e o tempo necessário para resolver. O tempo de resolução cresce ~ n^2, o que significa que leva 4-5 vezes mais para resolver um cubo que é 2x maior em cada dimensão.
Um cubo em camadas de 1024 pode ser resolvido em cerca de 1,5 segundos. Um cubo em camadas de 16384 pode ser resolvido em cerca de 20 minutos.
YouTube: resolvendo 65536 camadas do YouTube: resolvendo 32768 camadas
Imagem da face frontal de um cubo 32768
Resolve os centros depois os cantos e depois as bordas
Os centros são resolvidos em 15 estágios, onde cada estágio move todos os pedaços de uma certa cor de uma face para o rosto desejado. Por exemplo: um palco move todas as peças verdes no rosto branco para o rosto verde. Repita isso para todas as cores e rostos.
O solucionador usa o comutador descrito aqui, que pode comutar peças centrais de um quadrante de um rosto para um dilema em outro rosto. Uma propriedade muito importante desse comutador é que pode ser modificado para mover muitas peças em uma única linha ao mesmo tempo. Para cubos muito grandes, isso significa que ele pode mover centenas, senão milhares de peças em uma única operação. O número médio de movimentos k = (2 * p + 5) / p onde p é o número de peças que podem ser movidas por operação. K se aproxima rapidamente 2 à medida que o tamanho do cubo aumenta.
Os cantos são resolvidos usando um método básico de força bruta para mover o canto para dentro e depois girar até que as faces fossem orientadas corretamente. Will Smith pode explicar: https://www.youtube.com/watch?v=wbzkdrc9vqs
As bordas são resolvidas movendo cada par de bordas para a face da frente e trocando as peças desejadas da borda esquerda para a borda direita. Várias funções, quando necessário para corrigir ou impedir problemas de paridade.
As rotações de rosto são essencialmente livres. Em vez de mover todas as peças em uma determinada face (n^2 peças) para executar uma rotação, o solucionador simplesmente altera o sistema de coordenadas que é usado para ler/gravar no rosto. Isso economiza uma enorme quantidade de troca de dados.
// Virtually rotate this face by q * 90 degrees
inline void Face::RotatefaceCW ( const int q)
{
orientation = (orientation + q) & 3 ;
}
// Gets the value of this face at coordinates r = row, c = column
inline const byte Face::GetRC ( const uint r, const uint c) const
{
switch (orientation) {
case 0 :
return data[(r << BS) + c];
case 1 :
return data[(c << BS) + (R1 - r)];
case 2 :
return data[((R1 - r) << BS) + (R1 - c)];
case 3 :
return data[((R1 - c) << BS) + r];
default :
return 0 ;
}
}Este código inclui um exportador de imagem simples que é usado renderiza cada face em uma imagem.
https://www.nayuki.io/page/tiny-png-ultput
https://github.com/nayuki/nayuki-web-published-code
A pequena saída PNG é uma pequena biblioteca independente, disponível em C e C ++, que leva Pixels RGB8.8.8 e grava um arquivo PNG.
The total number of moves can be estimated using a simple formula. Supondo que o cubo seja suficientemente randomizado, podemos esperar que o primeiro rosto seja 1/6 resolvido e, portanto, 5/6 das peças deverão ser movidas. The second face will be 1/5 solved and require 4/5 of the pieces to be moved. The third face 3/4, Fourth face 2/3, Fifth face 1/2 and the last face will be completely solved. The average number of moves (k) to move single piece can be estimated experimentally as ~2.1. O valor de K diminui à medida que o tamanho do cubo aumenta. O valor nunca pode ser menor que 2, pois o comutador exige que cada peça seja movida pelo menos 2 vezes.
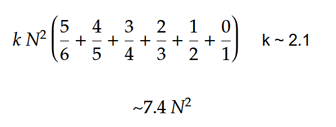
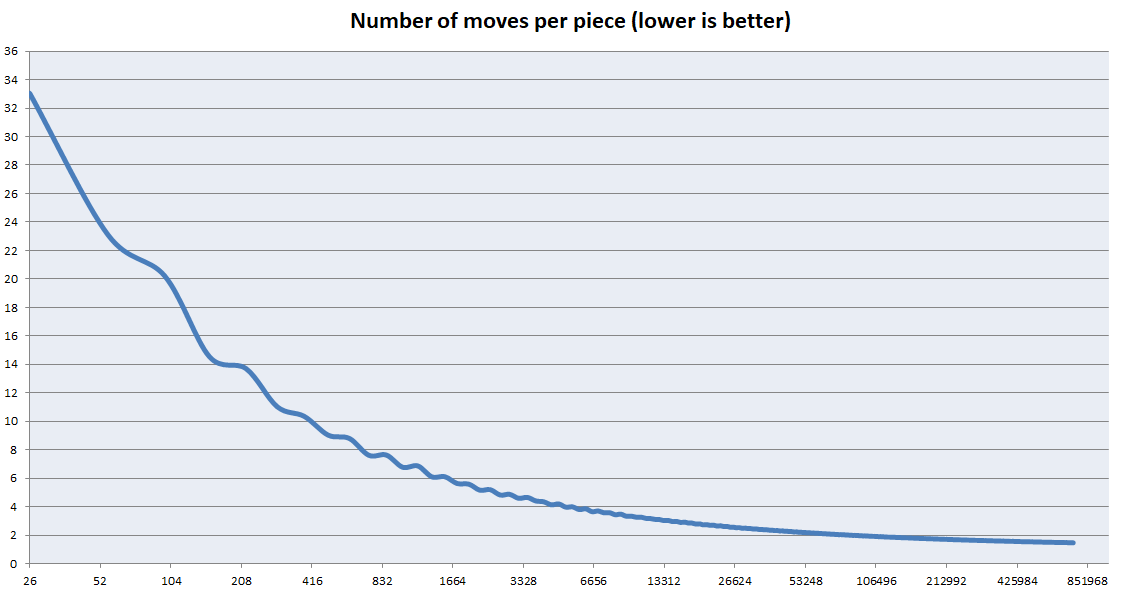
Esse algoritmo é otimizado para cubos muito grandes. No entanto, é terrível para pequenos cubos. As principais otimizações foram focadas em resolver os centros o mais rápido possível e nenhuma consideração foi dada para resolver as bordas. No entanto, o tamanho das bordas é insignificante em comparação com os centros à medida que o tamanho do cubo aumenta. O gráfico abaixo mostra como o número médio de movimentos por peça diminui com cubos maiores. Nota: Este não é um gráfico de k. É um gráfico de (totais movimentos) / (número de peças)
cmake -B build -S .
cd build
cmake --build .
RCube/RCube